ねじ設計計算式
1．形状・物性計算編
1．1．ねじ山寸法
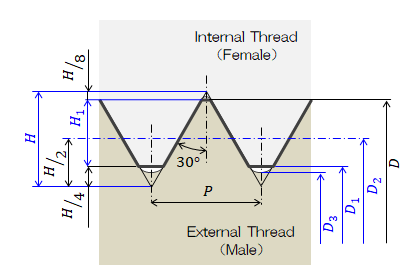
呼び径\( D \)、ねじピッチ\( P \)から以下の寸法を計算します。| 項目 | 記号 |
|---|---|
とがり山高さ |
\( H = P \cos 30°\)
|
| ひっかかり 高さ |
\( H_1 = H - \displaystyle \left( \frac{ H }{ 8 } + \frac{ H }{ 4 } \right) \) |
| めねじ内径 | \( D_1 = D - 2 H_1 \) |
| ねじ有効径 | \( D_2 = D - 2 \times \displaystyle \frac{ 3 }{ 8 } H\) |
| おねじ 谷底径 |
\( D_3 = D - 2 H \displaystyle \left( 1 - \frac{ 1 }{ 8 } - \frac{ 1 }{ 6 } \right) \) |
| おねじ有効 断面積径 |
\( D_4 = \displaystyle \frac{ D_2 + D_3 }{ 2 } \) |
|
|
※：計算方法はJIS B 0205（ISO 68-1）に従います。
1．2．座面有効径
接触座面の形状に応じた等価円径（＝座面有効径）\( D_{fle} \) を計算します。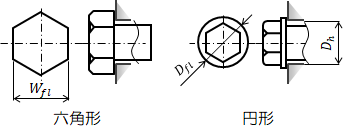
座面形状は円形または六角形が一般的で、それぞれの接触面径を\( D_{flo} \) で表すとき、
\[
\begin{eqnarray}
D_{flo}
=
\begin{cases}
& D_{fl} \quad ( 円形 )
\\
& \displaystyle \sqrt{ \frac{ 2 \sqrt{ 3 } }{ \pi } } W_{fl} \quad ( 六角形 )
\end{cases}
\end{eqnarray}
\]
座面有効径の計算式は次のようになります。
\[
D_{fle}
=
\frac{ 2 }{ 3 } \frac{ D_{flo}^3 - D_h^3 }{ D_{flo}^2 - D_h^2 }
\]
上記計算式の導出方法は、当サイト等価物理量ページを参照ください。
1．3．ねじ噛合い長さ
次のおねじとめねじのかみあい長さを算出する方法について、それぞれ説明します。- ボルト・タップ穴締結
- ボルト・ナット締結
- 被締結体の挟み込み数最大5枚まで
- 不完全ねじ部は考慮しない
（1）ボルト・タップ穴締結
下記計算式によってかみあい長さを算出します。 また、かみあい長さが適当かどうかの判定も行います。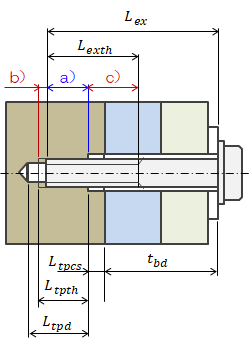
| 被締結体厚さ合計（被締結体ざぐり含む） |
|---|
| \( t_{bd} = \sum_i t_{bdi} + L_{tpcs} \) |
| おねじ軸部長さ |
| \( L_{exax} = L_{ex} - L_{exth} \) |
| おねじの被締結体からの突き出し量 |
| \( L_{out} = L_{ex} - t_{bd} \) |
| おねじ・めねじ噛合い長さ |
| \( L_{eng} = L_{tpth} - \min ( L_{out}, L_{exth} \ ) \) |
かみあいに対する判定を以下のように行います。
\(
L_{out}\leq
0
\)
\(
L_{ex}\geq
t_{bd} + L_{tpd}
\)
\(
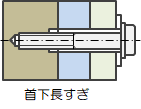
L_{exax}\geq
t_{bd}
\)
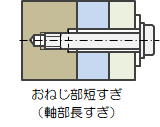
（2）ボルト・ナット締結
下記計算式によってねじ部の突出長を算出します。 また、突出長が適当かどうかの判定も行います。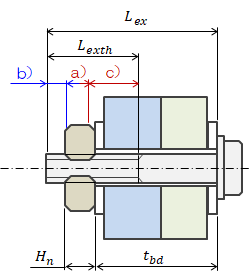
| 被締結体厚さ合計（被締結体ざぐり含む） |
|---|
| \( t_{bd} = \sum_i t_{bdi} + L_{tpcs} \) |
| おねじ軸部長さ |
| \( L_{exax} = L_{ex} - L_{exth} \) |
| おねじの被締結体からの突き出し量 |
| \( L_{out} = L_{ex} - t_{bd} \) |
| おねじ・めねじ噛合い長さ |
| \( \begin{align} L_{eng} = & \min ( L_{ex}, t_{bd} + H_n \ ) \\ & - \max ( L_{exax}, t_{bd} \ ) \end{align} \) |
かみあいに対する判定を以下のように行います。
\(
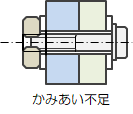
L_{out}\leq
0
\)
\(
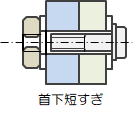
L_{ex}\leq
t_{bd} + H_{n}
\)
\(
L_{exax}\geq
t_{bd}
\)
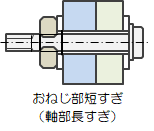
1．4．ばね定数
おねじ（ボルト）と被締結体のばね定数、内外力比、ヘタリ係数を算出します。これらは締結体に外力が作用した際の軸力影響を考慮するのに必要となります。
ボルトで締結体を締め付けると、ボルトは伸び、被締結体は圧縮されます。 この状態は、ボルトを引張りばね、被締結体を圧縮ばねと置き換えることができます。 この変形に際し締結部に生じる力を“軸力”と呼びます。 特に弾性範囲内においてボルトの伸び量・被締結体の縮み量と軸力の間には線形関係が成り立ちます。
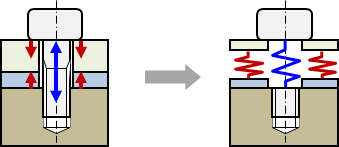
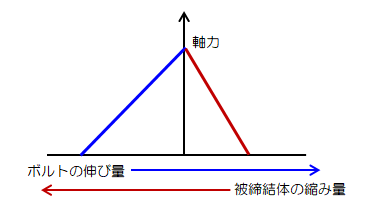
図1.4-1 軸力とボルト弾性伸び・被締結体圧縮縮みの関係図
（1）ボルトのばね定数計算
ボルトを次のように分割することでそれぞれのばね定数を求め、それらを直列につないだものとしてボルト全体のばね定数を算出します。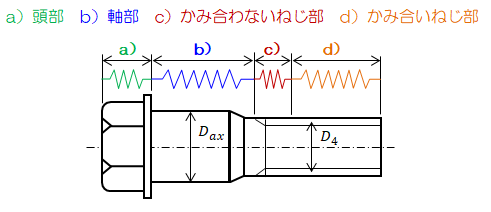
| \( E_{ex} \) | ：ボルトの縦弾性係数 |
| \( D_{ax} \) | ：軸部径 |
| \( D_{4} \) | ：ねじ部有効断面積径 |
| \( L_{i} \) | ：各部長さ |
\[
K_a
=
\frac{ \pi D_{ax}^2 E_{ex} }{ 4 ( 0.6 D ) }
\quad 、
K_b
=
\frac{ \pi D_{ax}^2 E_{ex} }{ 4 L_b }
\]
\[
K_c
=
\frac{ \pi D_{4}^2 E_{ex} }{ 4 L_c }
\quad 、
K_d
=
\frac{ \pi D_{4}^2 E_{ex} }{ 4 ( 0.7 D ) }
\]
これらより、ボルトのばね定数は
\[
\frac{ 1 }{ K_{ex} }
=
\sum_{i=a,b,c,d} \quad \frac{ 1 }{ K_i }
\]
になります。
（2）被締結体のばね定数計算
各被締結体ばねの定数\( K_{bdi} \)は次式で求まります。なお、添字\( i \)は被締結体の番号になります。\[
K_{bdi}
=
\displaystyle \frac{ \pi E_{bdi} }{ 4 t_{bdi} }
( D_e^2 - D_{bdh}^2 \ )
\]
\( E_{bdi} \):縦弾性係数、 \( t_{bdi} \):被締結体の厚さ、 \( D_{bdh} \):被締結体の穴径
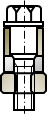
この式に含まれる\( D_e \)は軸力の作用する有効径と見ることができます。 その作用は被締結体の外径\( D_{bdo} \) と座面外径\( D_{fl} \)の関係によって、次の三つに場合分けされます。
|
\(
a) \
D_{bdo}\lt
D_{fl}
\)
被締結体は一様に圧縮される |
|
|
\(
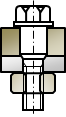
b) \
D_{fl}\leq
D_{bdo}\leq3D_{fl}
\)
被締結体は一様に圧縮される |
|
|
\(
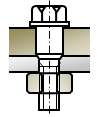
c) \
3D_{fl}\lt
D_{bdo}
\)
被締結体は一様に圧縮される |
|
この考え方に基づき、\( D_e \)を次式で定義します。
\[
\begin{eqnarray}
D_e
=
\begin{cases}
D_{bdo}
\
& ( D_{bdo} \lt D_{fl} ）
\\
D_{fl} + \alpha_f \displaystyle \frac{ k }{ 10 } \sum_i t_{bdi}
\
& ( D_{fl} \leq D_{bdo} ）
\end{cases}
\end{eqnarray}
\]
ここで\( \alpha_f \)と\( k \)を決める必要があります。\( k \)については次の二つの場合に分けて決定します。
\( b) \ D_{fl}\leq D_{bdo}\leq3D_{fl} \) のとき、 \( k = 1 - \displaystyle \frac{ 1 }{ 4 } \left( 3 - \frac{ D_{bdo} }{ D_{fl} } \right)^2 \)
\( c) \ 3D_{fl}\lt D_{bdo} \) のとき、 \( k=1 \)
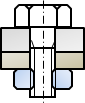
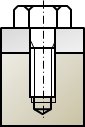
\( \alpha_f \)は締結方法によって決まる係数で、次のように場合分けできます。
| ボルト・ナット締結 | ボルト・タップ穴締結 |
|---|---|
|
|
| \( \alpha_f = 1 \) | \( \alpha_f = 2 \) |
\[
\displaystyle
\frac{ 1 }{ K_{bd} }
=
\displaystyle
\sum_{i = 1,2,\cdots}
\frac{ 1 }{ K_{bdi} }
\]
（3）内外力比
締結体に引張り荷重\( F_t \)が作用するとボルト軸部はさらに\( \lambda \)伸び、被締結体も\( \lambda \)縮み量が減ります。 そこで、引張り荷重が作用していないときの軸力を\( F_{ax} \)としたとき、\( F_t \)の作用は力のつり合いから次のように表せます。\[
\begin{align}
& \begin{cases}
F_t = F_{ex} - F_{bd}
\\
F_{ex} = F_{ax} + K_{ex} \lambda
\\
F_{bd} = F_{ax} - K_{bd} \lambda
\end{cases}
\\
\\
\rightarrow
\
& F_{ex}
=
F_{ax} + \frac{ K_{ex} }{ K_{ex} + W_{bd} } F_t
=
F_{ax} + \phi F_t
\end{align}
\]
この結果から、ボルトに外力\( F_t \)が作用してもその一部\( \phi F_t \)だけ付加されます。
このときの係数\( \phi \)を“内外力比”と呼びます。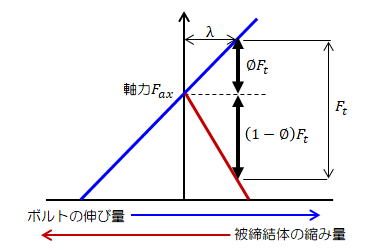
\[
\phi
=
\frac{ K_{ex} }{ K_{ex} + K_{bd} }
\]
（4）ヘタリ係数計算
弾性範囲内で軸力\( F_{ax} \)の大きさを変化させれば、各ばね定数\( K_{ex}, \ K_{bd} \)に比例してボルトの伸び量\( \delta_{ex} \)被締結体の縮み量\( \ \delta_{bd} \)が変化します。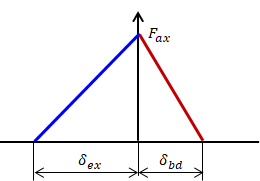
\[
\delta_{ex} = \frac{ F_{ax} }{ K_{ex} }
\ , \
\delta_{bd} = \frac{ F_{ax} }{ K_{bd} }
\]
従って、締結体全体の変形量\( \delta \)もまた軸力\( F_{ax} \)と線型関係にあります。
このとき得られる比例定数\( Z \)を“ヘタリ係数”と呼びます。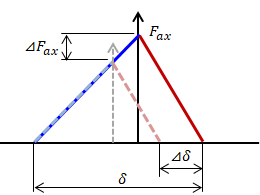
\[
\delta
=
\delta_{ex} + \delta_{bd}
=\frac{ K_{ex} + K_{bd} }{ K_{ex} K_{bd} } F_{ax}
\ \leftrightarrow \
F_{ax} = Z \delta
\]
\[
\therefore \
Z =
\frac{ K_{ex} K_{bd} }{ K_{ex} + K_{bd} }
\]
