2.等価摩擦径
2.1.等価摩擦径の概念
等価摩擦径とは、「円環状に面接触している領域に摩擦力によるトルクが発生するとき、トルク算出に必要となるモーメント長を面積領域のある代表的な1つの径に置き換え、トルクの一般式で求められるようにしたもの」にです。実際、面接触部に発生するトルクを計算するには、接触部を微小領域(面積素片)に分割して各部のトルクを計算し、それを全領域で積分しなければなりません。 それに対し、等価摩擦径という概念を用いることによって、面接触のトルクを積分することなく算出できるようになります。
以上の内容から、等価摩擦径が適用される実例として、ねじの座面トルク*)やクラッチ、ブレーキ等のトルク計算等が挙げられます。
*):JISの等価摩擦直径の定義は、外径と内径の平均値に変更されています。
ところで、この等価摩擦径は様々な文献において数式のみが提示され、その算出方法について触れられているものはあまりありません(あまりに簡単な概念だから?)。 そこで、本サイトではこの等価摩擦径の導出方法について見ていくものとします。
2.2.等価摩擦径の導出方法
等価摩擦径導出にあたり、まずは下図2-1のような平面上の円環接触の場合を考えます(例えば、ねじ座面等が相当します)。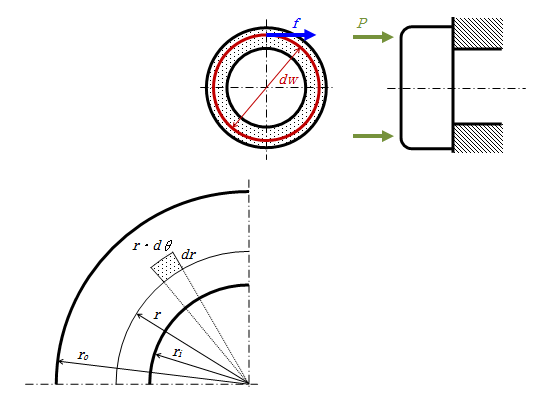
図2-1 接触部条件
計算の前提条件として、接触面に働く垂直荷重と摩擦係数がその全域で均一と仮定します。 そこで、接触面に働く単位面積あたりの垂直荷重(つまり面圧)をPとします。このとき、上図の半径rの位置にある面積素片(上図点部)に着目します。 この面積素片に働くトルクは次のようになります。
| 面積素片の面積 | \( dS = r d\theta \cdot dr \) |
| 面積素片に働く摩擦力 | \( df = \mu P \cdot dS \) |
\[
\begin{eqnarray}
dT
& = &
rdf
\\
& = &
\mu \cdot P \cdot r^2 d\theta dr
\tag{2-1}
\end{eqnarray}
\]
(2-1)式はモーメント長、つまり半径rの重み付けが考慮されており、半径rが変化すれば面積素片のトルクも変化します。
この面積素片のトルクdTを内外径に囲まれた範囲(ri ~ro )で積分すれば、接触面全域に発生するトルクが計算できます。\[
\begin{eqnarray}
T
& = &
\int_{r_{i}}^{r_{o}} \int_{0}^{2\pi} \mu \cdot P \cdot r^2 d\theta dr
\\
& = &
\mu \cdot P \int_{r_{i}}^{r_{o}} \int_{0}^{2\pi} r^2 d\theta dr
\\
& = &
\frac{2}{3}\pi (r_{o}^3 - r_{i}^3) \mu \cdot P
\end{eqnarray}
\tag{2-2}
\]
ここで次のように考えることで、等価摩擦直径を定義出来ます。
(2-2)式によって求めた接触部のトルクTを接触部面積\( S=\pi(r_{o}^2 - r_{i}^2) \)で割り、単位面積あたりのトルクとして計算します。\[
\frac{T}{S}
=
\frac{2(r_{o}^3-r_{i}^3)}{3(r_{o}^2-r_{i}^2)} \ \mu P
\tag{2-3}
\]
接触部に働く垂直荷重はF =PSゆえ、上式(2-3)は次のように書き換えられます。
\[
T
=
\frac{2(r_{o}^3-r_{i}^3)}{3(r_{o}^2-r_{i}^2)} \ \mu F
\tag{2-4}
\]
この(2-4)式は、“トルク=モーメント長×力”という一般式の形になっていることがわかります。
そこで、モーメント長に相当する項を次のパラメータで置き換えれば、\[
r_w
=
\frac{2(r_{o}^3-r_{i}^3)}{3(r_{o}^2-r_{i}^2)}
\tag{2-5}
\]
(2-4)式は次のように書き換えることができます。\[
T
=
r_w \mu F
\tag{2-6}
\]
(2-6)式は、「接触面に働く摩擦力μFが、見かけの半径rwの円周上に作用してトルクを発生させている」と考えることができます。
この半径rwを等価摩擦半径と言います。ここまでは、2次元平面上の円環接触に対する等価摩擦径を導出しました。
同様にして、円錐台面での等価摩擦径も導出できますので、簡単にさわりだけ説明しておきます。 円錐の半頂角をαとします。 円錐台面上に面積素片とると、その面積素片に働くトルクは次のようになります。
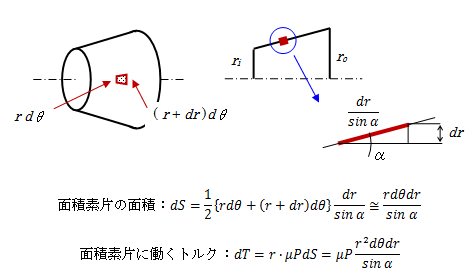
図2-2 円錐面での等価摩擦径
これを範囲(ri~ro)で積分すれば、接触面全域に発生するトルクが計算できます。\[
T
=
\frac{2}{3}\pi(r_o^3-r_i^3)\frac{\mu P}{\sin \alpha}
\]
また、円錐台の側面積は次のようになります。\[
S
=
\frac{\pi(r_o^2-r_i^2)}{\sin \alpha}
\]
以上から等価摩擦半径を求めると、結局平面のときと同じ(2-5)式になります。\[
r_w
=
\frac{2(r_{o}^3-r_{i}^3)}{3(r_{o}^2-r_{i}^2)}
\tag{2-5}
\]
2.3.等価摩擦直径の注意点
“等価~”を定義する場合、その目的を明確にし、適切な条件を設定する必要があります。 今回は円環状の接触部に発生するトルクを、一般式と同型で表すために等価摩擦径を定義しました。 この定義に際し、以下の3つの重要な仮定が存在します。| ・接触面は同心円のドーナツ型 | :形状依存 |
| ・摩擦力は接触面全域で均等に作用 | :作用力は定数 |
| ・トルクは接触面全域で均等に作用 | :接触面における平均化 |
等価摩擦径の適用において、この3つの仮定が成り立たない限り(2-7)式を単純に用いることは出来ません。 よって、その目的と条件を明確にすることで、適用の可否を判断し、適用できなければ新たな方法を模索していくことが必要になります。


