ねじ設計計算式
2．締結計算編
2．1．軸力低下
以下に示す非回転ゆるみによる軸力低下量を算出します。- 締結部の接触面凹凸変形によるなじみ、ヘタリによる軸力変化
- 締結時温度と使用時温度が異なるときの熱膨張差による軸力変化
- その他、指定ヘタリ量に応じた軸力変化
\[
\Delta F_{ax}
=
Z \delta
\]
各項目の軸力変化は、同時に作用するとして足し合わせます。（1）なじみ、ヘタリによる軸力変化
締結部の接触面凹凸の大きさは“最大高さ面粗度\( R_z \)”（表面粗さ）で指定します。 凹凸変形割合（つぶれ係数）\( C_{surf} \ \)については、表面加工方法に応じて次の三種類の方法で指定します。| 指定方法 | つぶれ係数 |
|---|---|
| 研削 | 0.46 |
| 旋削 | 0.3 |
| 任意指定 | 指定値 |
| なじみ量： | \( \delta_1 = C_{surf} \ ( R_{zi} + R_{zj} ) \) |
| 軸力低下量： | \( \Delta F_{ax1} = Z \delta_1 \) （Z：ヘタリ係数） |
（2）熱膨張差による軸力変化
ボルトと非締結体の材質が異なれば、線膨張係数の違いにより熱膨張差が生じます。 各被締結体厚さ\( t_{bdi} \)、線膨張係数\( \alpha_{bdi} \)、ボルトの線膨張係数\( \alpha_{ex} \)とするとき、| 熱膨張差： | \( \delta_2 = \sum_i \alpha_{bdi} \ t_{bdi} - \alpha_{ex} \sum_i t_{bdi} \) |
| 軸力低下量： | \( \Delta F_{ax2} = Z \delta_2 \) （Z：ヘタリ係数） |
2．2．必要最小軸力
締結の主な目的は「部品間の相対位置を変化させないこと」で、次の二つを守ることです。- 部品どうしが遊離（口開き）せず結合
- 部品どうしが滑らず結合
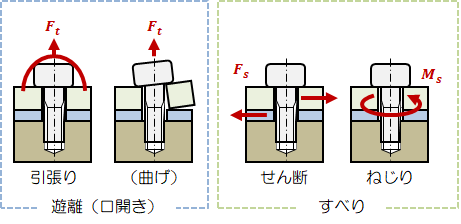これらは軸力を適切に設定すれば生じません。
そのために必要な軸力の算出を行います。（1）被締結体の遊離
1.4節で見たように、締結体に外力が作用しても軸力の影響でその一部\( \phi F_t \)しか付加されません。 ところが、外力がある値を超えると軸力の影響はなくなり、外力がそのまま付加されるようになります。
これは“\( ( 1 - \phi ) F_t \leq F_{axt} \)”になると、被締結体の圧縮効果がなくなるためです。
従って、被締結体を遊離させないために必要な最小軸力は以下で決まります。
\[
F_{axt} = ( 1 - \phi ) F_t
\]
（2）被締結体のすべり
被締結体は、ボルトの座面とめねじの座面に挟み込まれており、そのせん断方向は接合面の摩擦力によって保持されます。 被締結体をすべらせる方法は次の二通りあります。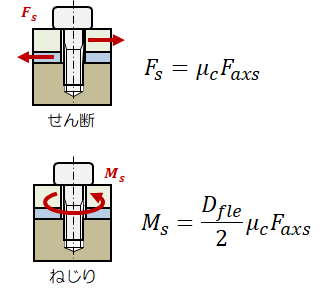
このとき、被締結体をすべらせないために必要な軸力\( F_{axs} \)は以下で決まります。
\[
F_{axs} = \max \left( \frac{ F_s }{ \mu_c } , \ \frac{ 2 M_s }{ \mu_c D_{fle} } \right)
\]
（3）最低残存軸力
（1）、（2）の軸力はその瞬間口開きやすべりが発生するため余裕がありません。 通常は安全マージンを確保するため、最低残存軸力\( F_{axres} \ \)を設定し、上乗せします。2．3．遊離・すべり荷重
設定した軸力によって以下の事象が発生しないことを確認します。- 部品どうしが遊離（口開き）しない
- 部品どうしがすべらない
ただし、複合作用についてはここでは見ないものとします。
2．4．締付トルク簡易版
以下の内容を、簡易的に計算します。- 軸力から締付トルクを計算
- 締付トルクから軸力を計算
締付トルク：\( T_f = k D F_{ax} \)[N・m]
（\( k \)：トルク係数、D：呼び径[mm]、\( F_{ax} \)：軸力[kN]）
また、簡易的に締付応力を次式より算出します。
\[
\sigma_{eq}
=
\frac{ T_f }{ 0.0425 \left( 1 + \displaystyle \frac{ 1 }{ Q_{tq} } \right) D^3 }
\]
（\( Q_{tq} \)：締付トルク係数、本サイトWebアプリでは\( Q_{tq} = 1 \)で計算）
