ねじ設計計算式
2.5.締付トルク詳細版
以下の内容を計算します。- 軸力から締付トルクを計算
- 締付トルクから軸力を計算
- 締付トルク または 軸力
- 座面トルク
- ねじ面トルク(締り側 / 緩み側)
- 緩み判定
- 締付応力
(1)締付トルク計算式
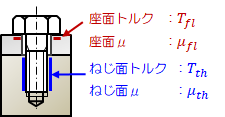
座面トルク |
\( T_{fl} = D_{fle} \mu_{fl} \displaystyle \frac{ F_{ax} }{ 2 } \) |
|---|---|
| ねじ面トルク (締り側) |
\( T_{thf} = \left( \displaystyle \frac{ D_2 }{ \cos \alpha } + \frac{ P }{ \pi } \right) \displaystyle \frac{ F_{ax} }{ 2 } \) |
| ねじ面トルク (緩み側) |
\( T_{thf} = \left( \displaystyle \frac{ D_2 }{ \cos \alpha } - \frac{ P }{ \pi } \right) \displaystyle \frac{ F_{ax} }{ 2 } \) |
\[
\begin{align}
T_{f}
& =
T_{fl} + T_{thf}
\\
& =
\left(
D_{fle} \mu_{fl} +
\displaystyle \frac{ D_2 }{ \cos \alpha } + \frac{ P }{ \pi }
\right) \displaystyle \frac{ F_{ax} }{ 2 }
\end{align}
\]
(2)緩み判定
ねじ面でのすべり発生が緩みにつながる、と考えられます。
\( T_{fl} \gt T_{thf} \)
ねじ面でのすべりは発生しない
緩まない
\( T_{thl} \gt T_{fl} \)
ねじ面で、緩み/締り両方向のすべりが発生する
緩む可能性あり
\( T_{thf} \geq T_{fl} \geq T_{thl} \)
ねじ面で緩み方向のすべりのみが発生する
緩む
(3)締付応力計算
締付時には次の荷重による応力が同時に発生します。| 荷重 | 発生部位 | 発生応力 |
|---|---|---|
| 軸力\( F_{ax} \) | ボルト軸部 | 引張り応力 \( \sigma_{tf} \) |
| おねじ部 | ねじ山せん断応力 \( \tau_{thex} \) | |
| めねじ部 | ねじ山せん断応力 \( \tau_{thin} \) | |
| 締付トルク\( T_{f} \) | ボルト軸部 | ねじり応力 \( \tau_{tf} \) |
等価応力\( \sigma_{eqtf} \ \)は次式で計算し、これが引張り降伏\( \sigma_y \)より大きいことが言えればよい、とします。
\[
\sigma_{eqtf}
=
\sqrt{
\sigma_{tf}^2 + C_{eq} \tau_{tf}^2 }
\gt
\sigma_y
\]
(\( C_{eq} \):等価応力係数)
応力計算式については別章で説明します。
2.6.締付トルク範囲
座面とねじ面摩擦係数のばらつきを考慮した締付トルク範囲を算出します。 前提条件は次の通りとします。- 必要最小軸力\( F_{axo} \)を担保する
- ボルトは降伏しない
- 摩擦係数ばらつきは正規分布に従う
- 軸力範囲
- 締付トルク範囲
- 緩み判定(座面トルク、ねじ面トルク(締り側 / 緩み側)を含む)
- 締付応力
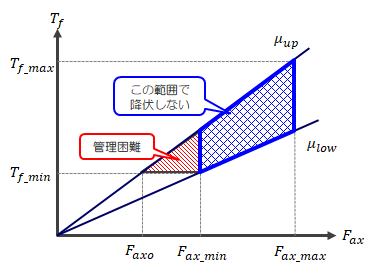
(1)締付トルク範囲決定フロー
- 必要最小軸力\( F_{axo} \ \)から最小締付トルク\( T_{fmin} \ \)を決める
- \( T_{fmin} \ \)に対し\( \mu_{low} \)での軸力\( F_{axmin} \ \)を算出する
- \( F_{axmin} \ \)に対して\( \mu_{up} \)での締付トルク\( T_f' \)を算出する
- \( T_f' \)に対して\( \mu_{low} \)での軸力\( F_{axmax} \ \)を算出する
- 降伏する軸力\( F_{axy} \ \)に対し、\( F_{axmax} \gt F_{axy} \ \)なら、\( F_{axmax} = F_{axy} \ \)とする
- \( F_{axmax} \ \)に対して\( \mu_{up} \)での締付トルク\( T_{fmax} \ \)を算出する
(2)摩擦係数の感度
座面トルクとねじ面トルクを、それぞれの摩擦係数で偏微分すれば感度が分かります。座面トルク |
\( \displaystyle \frac{ \partial T_{fl} }{ \partial \mu_{fl} } = \frac { D_{fle} F_{ax} }{ 2 } \ \rightarrow \ d T_{fl} = \frac{ D_{fle} F_{ax} }{ 2 } d \mu_{fl} \) |
|---|---|
| ねじ面トルク | \( \displaystyle \frac{ \partial T_{thf} }{ \partial \mu_{th} } = \frac { D_{2} F_{ax} }{ 2\cos \alpha } \ \rightarrow \ d T_{thf} = \frac{ D_{2} F_{ax} }{ 2\cos \alpha } d \mu_{th} \) |
\[
\begin{align}
d T_f
=
\sqrt{ dT_{fl}^2 + dT_{thf}^2 }
\end{align}
\]
(3)締付トルクと軸力の計算
強度の観点を抜いて、(1)の締付トルク範囲決定フローに従い計算を行います。そこで、
\[
\begin{align}
&
D_5
=
\displaystyle \frac{ D_2 }{ \cos \alpha }
\\
&
\Theta
=
D_{fle} \ \mu_{fle}
+ D_5 \mu_{th}
+ \frac{ P }{ \pi }
\\
&
d C_{fth}
=
\sqrt{
( D_{fle} \ d \mu_{fl} )^2 + ( D_5 d \mu_{th} )^2
}
\end{align}
\]
とおいて順に計算します。まずは\( T_{fmin} \)から計算を始めます。
\[
T_{fmin}
=
( \Theta + dC_{fth} \ ) \frac{ F_{axo} }{ 2 }
\]
この\( T_{fmin} \)を使って
\[
F_{axmin}
=
\frac{ 2 T_{fmin} }{ ( \Theta - dC_{fth} ) }
\]
この\( F_{axmin} \ \)を使って
\[
T_{f1}
=
( \Theta + dC_{fth} \ ) \frac{ F_{axmin} }{ 2 }
\]
この\( T_{f1} \)を使って
\[
F_{axmax}
=
\frac{ 2 T_{f1} }{ ( \Theta - dC_{fth} ) }
\]
この\( F_{axmax} \ \)を使って
\[
T_{fmax}
=
( \Theta + dC_{fth} \ ) \frac{ F_{axmax} }{ 2 }
\]
(4)締付応力
前頁で求めた最大軸力\( F_{axmax} \ \)時の発生等価応力\( \sigma_{eq} \)が降伏応力\( \sigma_y \)を超えた場合、\[
\sigma_{eq}
=
\sqrt{
\sigma_{tf}^2 + C_{eq} \tau_{tf}^2
}
\gt
\sigma_y
\tag{*}
\]
(\( C_{eq} \):等価応力係数)
最大軸力を降伏応力に相当する軸力に置き換える必要があります。そこで\( \sigma_y \)に対応する軸力\( F_{axy} \ \)を求めます。
応力は次式で計算できるので、
\[
\begin{align}
&
\sigma_{tf}
=
\frac{ 4 F_{axy} }{ \pi D_{min}^2 }
\\
&
\tau_{tf}
=
\frac{ 16 T_{thf} }{ \pi D_{min}^3 }
=
\frac{ 8 F_{axy} }{ \pi D_{min}^3 }
\left(
D_5 ( \mu_{th} + d \mu_{th} )
+ \frac{ P }{ \pi }
\right)
\end{align}
\]
これらを(*)式に代入して(計算過程は省略します)\[
F_{axy}
=
\frac{ \pi D_4^2 \sigma_y }
{ 4
\sqrt{
1 + C_eq
\biggl\{
\displaystyle \frac{ 2 }{ D_{min} }
\left(
D_5 ( \mu_{th} + d \mu_{th} )
+ \frac{ P }{ \pi }
\right)
\biggr\}^2
}
}
\]
(5)締付トルクと軸力の計算(その2)
強度の観点を入れて最大軸力と締付トルクを決定します。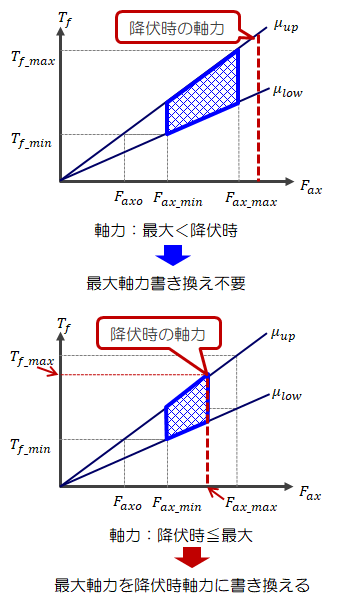
(6)締付不具合発生の判定
軸力が不足していると、被締結体の遊離(口開き)やすべりが発生します。 従って、設定軸力が適切がを判定する必要があります。
i)単体で荷重が作用する場合
\[
F_{ax}
\gt
\max \left(
( 1 - \Phi ) F_t
\ , \
\frac{ F_s }{ \mu_c }
\ , \
\frac{ 2 M_s }{ \mu_c D_{fle} }
\right)
\]
ii)複合で荷重が作用する場合
以上を満足すれば、被締結体の遊離やすべりは発生しません。
\[
\begin{align}
F_{ax}
\gt
&
( 1 - \Phi ) F_t
\\
& + \max \left(
F_{axt} - ( 1 - \Phi ) F_t
\ , \
\frac{ F_s }{ \mu_c }
\ , \
\frac{ 2 M_s }{ \mu_c D_{fle} }
\right)
\end{align}
\]


