弾性論
ヘルツの接触理論
接触する二つの物体に生じる圧力分布について、ハインリヒ・ヘルツが理論的に解析したものをヘルツの接触理論(1881年)と呼びます (論文原著:Über die Berührung fester elastischer Körper, H. Hertz はドイツ語ですので、気になる方は頑張って読んでみてください。私は断念しました)。ヘルツの接触理論は次の前提が設けられています。
- 変形は弾性限度内である
- 二つの物体間に相対的な滑りはなく、摩擦もない
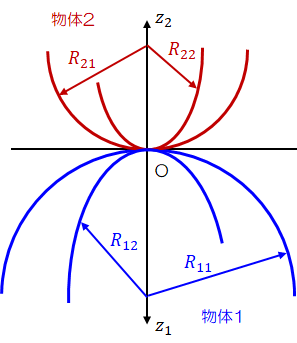
図1 無負荷時の接触
このとき、接触点近傍の物体の表面は次式で表せます。\[
z_1
=
A_{xx} \ x^2 + A_{xy} \ xy + A_{yy} \ y^2
( =
A_{ij} \ x_i x_j )
\\
z_2
=
B_{xx} \ x^2 + B_{xy} \ xy + B_{yy} \ y^2
( =
B_{ij} \ x_i x_j )
\tag{1}
\]
(\( A_{ij}, B_{ij} \ \)はテンソルになります)
それに対し接触点Oを通るz軸方向に圧縮力Fを掛けると、接触点O近傍で圧縮変形が生じ、微小距離hだけ接近し合うことになります。 このとき、圧縮変形によって生じる物体1、2の変位のz軸成分を\( u_{1z}, u_{z2} \)で表せば(下図参照)
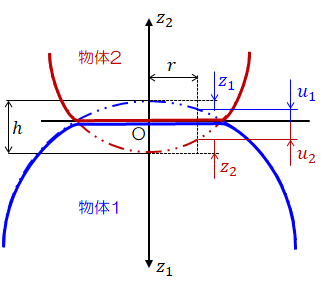
図2 負荷時の接触
上図からわかるように、接触域のすべての表面上の点で次の関係式が成り立ちます。\[
( z_1 + z_2 ) + ( u_1 + u_2 ) = h
\tag{2}
\]
(2)式に(1)式を代入して
\[
( A_{ij} + B_{ij} ) x_i x_j + ( u_1 + u_2 ) = h
\tag{3}
\]
を得ます。ここで、x軸とy軸をテンソル\( A_{ij} + B_{ij} \ \)の対角成分、つまり\( A_{xy} + B_{xy}, A_{yx} + B_{yx} \ \)が0になるよう設定します (このような設定は常に可能です)。 すると(3)式は次の簡単な形で表せます。
\[
A x^2 + B y^2 + ( u_1 + u_2 ) = h
\tag{4}
\]
ただし、A、Bは物体1、2の主曲率によって表される定数で、次の関係を持ちます。
\[
\begin{eqnarray}
& 2 ( A + B )
& =
\left(
\frac{1}{R_{11}} + \frac{1}{R_{12}} + \frac{1}{R_{21}} + \frac{1}{R_{22}}
\right)
\\
& 4 ( B - A )^2 \
& =
\left( \frac{1}{R_{11}} - \frac{1}{R_{12}} \right)^2
+ \left( \frac{1}{R_{21}} - \frac{1}{R_{22}} \right)^2
\\
& & \qquad \quad
+ 2 \cos 2 \varphi
\left( \frac{1}{R_{11}} - \frac{1}{R_{12}} \right) \left( \frac{1}{R_{21}} - \frac{1}{R_{22}} \right)
\end{eqnarray}
\tag{5}
\]
(\( \varphi \)は主曲率半径\( R_{11}, R_{21} \)を持つ曲面の法断面間角度)
さて、\( z_1 + z_2 \)は負にはならない(負になると突起ができる)ので、AとBはともに正でなければなりません。 従って、\( z_1 + z_2 \)が一定値をとるような点は楕円を形成します。
\[
z_1 + z_2 = A x^2 + B y^2
\]
図3 負荷時の接触面形状
ここで、物体1、2の縦弾性係数を\( E_1, E_2 \)、ポアソン比を\( \nu_1, \nu_2 \)とし、両物体の接触各点に働く圧力を\( P_z(x,y) \)とします。物体の曲率半径が接触面の境界径よりも十分大きいとき、接触面は平面近似できるので、物体1、2に生じる各点の変位\( u_{z1}(x,y), u_{z2}(x,y) \ \)は次のように表せます (この関係式は別ページで説明します(準備中))。
\[
u_{zi}(x,y)
=
\frac{ 1 - \nu_i ^2}{ \pi E_i} \iint \frac{ P_z( x', y' ) }{ r } dx' dy'
\quad ( i=1,2 )
\tag{6}
\]
\[
\left(
r = \sqrt{ (x-x')^2 + (y-y')^2 \ } \
\right)
\]
積分範囲については、接触域外の圧力\( P_z = 0 \)であることから接触域のみで行います。(6)式の結果から、接触によって生じる物体1と2の変位の比は一定値をとり、
\[
\frac{ u_{z1} }{ u_{z2} }
=
\frac{ ( 1 - \nu_1 ^2 ) E_2 }{ ( 1 - \nu_2 ^2 ) E_1 }
\tag{7}
\]
で表せます。この(7)式と(4)式によって変位の分布が決まります。
次に、(6)式を(4)式に代入して
\[
\frac{ 1 }{ \pi }
\left( \frac{ 1 - \nu_1 ^2}{ E_1 } + \frac{ 1 - \nu_2 ^2}{ E_2 } \ \right)
\iint P_z( x', y' ) \frac{ dx' dy' }{ r }
=
h - A x^2 -B y^2
\tag{8}
\]
を得ます。
この式は、接触面に沿った圧力分布\( P_z \)を与える積分方程式になります。
この解は、次の2つの事実の対比から得られます。
- 電荷(または質量分布)によって生じるポテンシャルの型と同じ
- 一様に電荷を受けている楕円体内部のポテンシャルは座標の2次関数
楕円体内部のポテンシャルについて、途中結果は数学的な内容によるので上記参考文献に委ねて結果のみ示します。
\[
\begin{eqnarray}
& \iint \sqrt{ 1-\frac{x'^2}{a^2}-\frac{y'^2}{b^2} } & \ \frac{ dx'dy' }{ r }
\\
& & =
\frac{ \pi a b }{ 2 }
\int_0^{\infty} \left(
1 - \frac{x^2}{a^2+\xi} - \frac{y^2}{b^2+\xi}
\right)
\frac{d \xi} { \sqrt{(a^2+\xi)(b^2+\xi)\xi}}
\end{eqnarray}
\tag{9}
\]
\[
\left(
r = \sqrt{ (x-x')^2 + (y-y')^2 \ } \
\right)
\]
この関係と(8)式を左辺同士、右辺同士を並べて書いて比較します。
- 左辺: \( \displaystyle \iint D P_z( x', y' ) \frac{ dx' dy' }{ r } \leftrightarrow \iint \sqrt{ 1-\frac{x'^2}{a^2}-\frac{y'^2}{b^2} } \ \frac{ dx'dy' }{ r } \)
- 右辺: \( h - A x^2 -B y^2 \leftrightarrow \displaystyle \frac{ \pi a b }{ 2 } \int_0^{\infty} \left( 1 - \frac{x^2}{a^2+\xi} - \frac{y^2}{b^2+\xi} \right) \frac{d \xi} { \sqrt{(a^2+\xi)(b^2+\xi)\xi}} \)
\[
\left(
D
=
\frac{ 1 }{ \pi }
\left( \frac{ 1 - \nu_1 ^2}{ E_1 } + \frac{ 1 - \nu_2 ^2}{ E_2 } \ \right)
\right)
\]
すると「左辺の積分は同型」、「ともに右辺はx,yの2次関数」であることから、次の結論が得られます。
- 接触域の境界:\( \displaystyle \frac{x^2}{a^2}+\frac{x^2}{b^2}=1 \)(楕円)
- 圧力分布関数:\(P_z(x,y)= \zeta \sqrt{ 1-\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}} \quad \) (\( \zeta \)は定数)
\[
F
=
\iint \zeta \sqrt{ 1-\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}} dx dy
\tag{10}
\]
そのためには次の積分を計算する必要があります。
\[
\begin{eqnarray}
& \iint \sqrt{ 1-\frac{x^2}{a^2}-\frac{y^2}{b^2} } \ dxdy
& =
\iint \sqrt{ 1-t^2 } \ \left| \frac{\partial (x,y)}{\partial(\theta, t)} \ \right| \ d\theta dt
\\
& & \qquad (x = ta \cos \theta, y= tb \sin \theta ,\frac{\partial (x,y)}{\partial(\theta, t)} = -abt)
\\
& & =
ab\iint t \sqrt{ 1-t^2 } \ d\theta dt
\\
& & =
2 \pi ab \int_0^1 t \sqrt{ 1-t^2 } \ dt
\\
& & =
\frac{2 \pi ab}{3}
\end{eqnarray}
\]
従って、
\[
F
=
\zeta \frac{2 \pi ab}{3}
\
\leftrightarrow
\
\zeta = \frac{3F}{2 \pi ab}
\]
が得られ、圧力分布関数\( P_z \)はx,yの二次関数で表せることができました。
\[
P_z(x,y)
=
\frac{3F}{2 \pi ab}\sqrt{ 1-\frac{x^2}{a^2}-\frac{y^2}{b^2} }
\tag{11}
\]
この結果から、接触部の最大圧力は接触中心で生じ、平均圧力\( F/ \pi ab \)の3/2倍になることがわかります。
しかし、圧力分布関数\( P_z \)は特定されたわけではなく、まだ接触楕円の長径2a、短径2bが決まりません。 そこで(11)式を(8)式に代入し、
\[
D
\iint \frac{3F}{2 \pi ab} \sqrt{ 1-\frac{x^2}{a^2}-\frac{y^2}{b^2} } \frac{ dx' dy' }{ r }
=
h - A x^2 -B y^2
\]
さらに左辺の積分項を(9)式のもので書き換えます。
\[
\frac{3 F D }{ 4 }
\int_0^{\infty} \left(
1 - \frac{x^2}{a^2+\xi} - \frac{y^2}{b^2+\xi}
\right)
\frac{d \xi} { \sqrt{(a^2+\xi)(b^2+\xi)\xi}}
=
h - A x^2 -B y^2
\tag{12}
\]
この式は任意のx、yについての恒等式になるため、x、yの係数、定数項がそれぞれ等しくなければなりません。
従って、次の関係が成り立ちます。
\[
\begin{eqnarray}
& A
& =
\frac{3 F D }{ 4 }
\int_0^{\infty} \frac{d \xi} { (a^2+\xi) \sqrt{(a^2+\xi)(b^2+\xi)\xi}}
\\
& B
& =
\frac{3 F D }{ 4 }
\int_0^{\infty} \frac{d \xi} { (b^2+\xi) \sqrt{(a^2+\xi)(b^2+\xi)\xi}}
\\
& h
& =
\frac{3 F D }{ 4 }
\int_0^{\infty} \frac{d \xi} { \sqrt{(a^2+\xi)(b^2+\xi)\xi}}
\end{eqnarray}
\tag{13}
\]
F,D,A,Bは既知なため、(13)の上2式の連立方程式からa、bを決まるはずです。
しかし残念ながら、このままではa、bは解けません。
そこでa、bを求めるために、次の補助変数\( \tau \)を導入します。
\[
\cos \tau
=
\frac{ B-A }{ A+B }
\tag{14}
\]
これは(5)式により簡単に算出できます。
さらに、この補助変数については完全楕円積分
\[
\begin{eqnarray}
& F
& =
\int_0^{\infty} \frac{ d \theta } { \sqrt{ 1 - k^2 \sin ^2 \theta }}
\\
& E
& =
\int_0^{\infty} \sqrt{ 1 - k^2 \sin ^2 \theta } \ d \theta
\end{eqnarray}
\tag{15}
\]
を用いて次のように表すこともできます。
\[
\cos \tau
=
\frac{ (2-k^2)E - 2(1-k^2)F }{ k^2E }
\tag{16}
\]
F、Eは第1種と第2種の完全楕円積分で、kを与えることで関数表から値は決まります。
ところが、k自身の決め方がこれではわかりません。
従って、実際の計算ではあらかじめ様々なkに対してF、Eを算出して\( \cos \tau \)をグラフ化したものが準備されていて、(14)式で求めた値と照らし合わせてkを決める、という方法がとられます。また、kを決める別の方法として、kの値を適当に変化させながら(14)式と(16)式が等しくなるよう反復計算することでも求められます (計算機による数値計算)。
\[
\frac{ B-A }{ A+B }
=
\frac{ (2-k^2)E - 2(1-k^2)F }{ k^2E }
\tag{17}
\]
以上からkが求まると、ようやく次式によってa、bが定まります。
\[
\begin{eqnarray}
& a
& =
\mu
\sqrt[ 3 \ \ \ ]{ \frac{ 3 \pi FD }{ 2A } }
, \quad
\mu
=
\sqrt[ 3 \ \ \ ]{ \frac{ 2E }{ \pi ( 1-k^2) } }
\\
& b
& =
\lambda
\sqrt[ 3 \ \ \ ]{ \frac{ 3 \pi FD }{ 2A } }
, \quad
\lambda
=
\sqrt[ 3 \ \ \ ]{ (1-k^2) \frac{ 2E }{ \pi } }
\end{eqnarray}
\tag{18}
\]
接触域の長径2a、短径2bが定まったことで、次の接触特性が算出できるようになります。
- 接触域の圧力分布:\( P_z(x,y) \)
- 接触域の変位分布:\( u_{zi}(x,y) \ (i = x,y ) \)
- 物体1、2の接近量:\( h \)
- 接触面積:\( \pi a b \)


