データ分析ツール（Excelアドイン）
フーリエ解析
本ページでは、Excelアドイン機能で行えるフーリエ変換の方法について説明します。 なお本サイトでは、Excelで行えるフーリエ変換ソフトも無料で公開しています。 そちらもご活用ください。Excelでは、フーリエ変換による時刻歴データの周波数分析が可能です。 また、逆変換も用意されていますので、周波数応答から時刻歴応答への変換も可能です。
ただし、Excelのフーリエ変換には次の制約があります。
- データ数は2n個でなければなりません。
- データ数は最大4096（212）個までとなります。
（0）サンプルファイル
フーリエ変換のサンプルとして、次のファイルを使用します。サンプルファイル：フーリエ変換サンプル.xls
サンプルファイルのフーリエ変換を行う時刻歴応答関数（サンプル関数）：\[
f(x)
=
a_1 \sin (n_{1} \omega t)
+ a_1 \sin (n_{2} \omega t)
+ a_2 \sin (n_{3} \omega t)
+ a_3 \sin (n_{4} \omega t)
\]
サンプルファイルの振幅、角速度（次数）のデフォルト設定値：
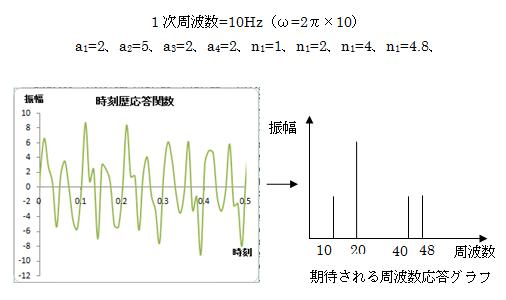サンプリング間隔は0.01sec、サンプリング数は1024個で解析します。
時刻歴データは、下図のように計算しています。
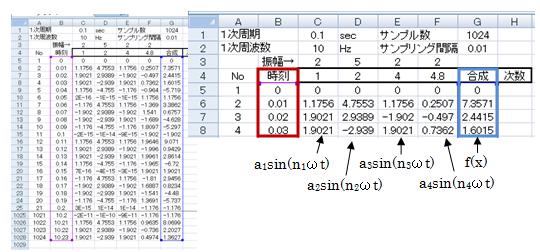
（1）周波数（横軸）の計算
Excelのフーリエ解析では周波数を計算しませんので、あらかじめ周波数列を以下の計算に基づき作成します 周波数列はExcelのI列になります）。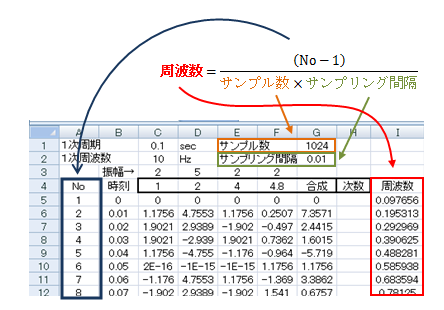
（2）データ／データ分析／フーリエ解析を選択
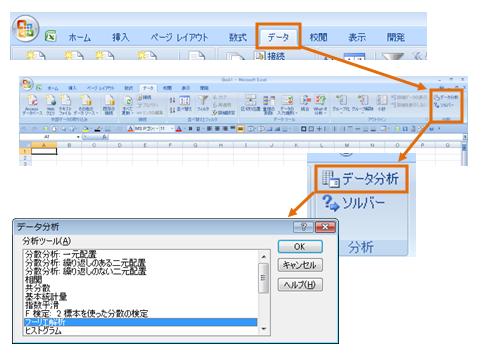
（3）フーリエ解析ダイアログの設定
ここではフーリエ変換を行いますので、入力範囲に「フーリエ変換する数値」の入ったセルを選択し、出力先に「変換データ」を出力する際の列の先頭セルを選択します。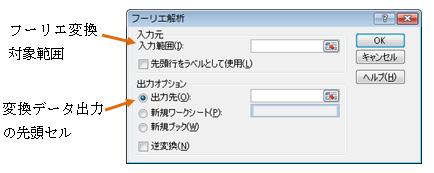
a）入力元
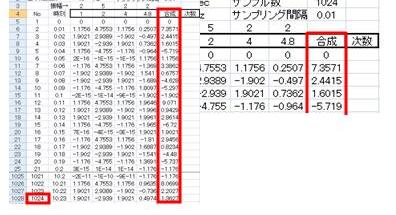
| 入力範囲 | フーリエ変換するセルを選択します。 その際、データの数は必ず2n個（n=1～12の整数）とします （最大4096個まで）。今回は1024個のデータで解析をしますので、 “合成”列（ExcelのG列＝関数f(x)）の数式入力セルを1024個選択します。 |
|---|---|
| データ方向 | 図1のように変数を入力すれば列を、図2のように変数を入力すれば行を選択します。 |
b）出力先
データの出力オプションを決めます。
今回は“出力先”を選択します。
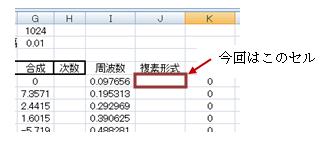
| 出力先 | 指定したセル（先頭セルのみでOK）にデータを出力します。 |
|---|---|
| 新規ワークシート | 新しくシートを作り、そこにデータを出力します。 入力はシート名になります。 |
| 新規ブック | 新しいファイルを作り、そこにデータを出力します。 |
（4）計算の実行
上記設定完了後“OK”ボタンをクリックすると計算が始まり、実行後の出力データは複素形式で表示されます。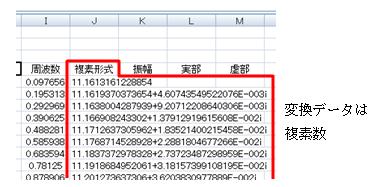
振幅の複素数表示を関数：IMABS（対象セル）によって、絶対値にします。
さらに、Excelではこの絶対値を（サンプル数÷2）で割る必要があります。
この複素数の絶対値に後処理をしたものが、各周波数帯における振幅になります。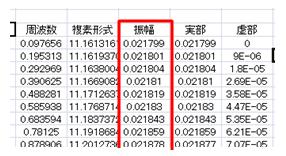
さて、変換された複素数の絶対値と周波数のセルを用いてグラフを作成します。
変換したデータすべて（1024個）をグラフに取り込むと次のようになります。
今回100Hzまで計算していますが、50Hzを境に対称形となってきます。
フーリエ変換する際に、波形を認識するのに必要な最小の周波数は、解析上の基本周波数の2倍であるためで、これをサンプリング定理と呼びます。\[
\begin{eqnarray}
基本周波数
& = &
\frac{1}{サンプル数 \times サンプリング間隔}
\\
& = &
周波数分解能
\end{eqnarray}
\]
つまり解析可能な最大周波数は、“基本周波数×サンプル数／2”となります。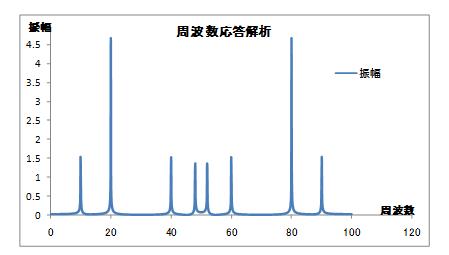
よって、解析結果としては0～50Hzの周波数帯を採用すれば良く、それ以上のデータについては不要になります。
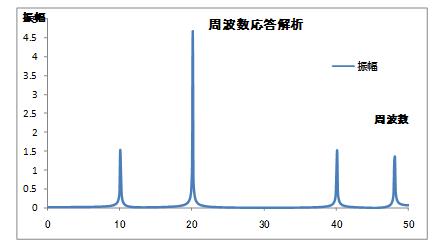このグラフは前述した「期待される周波数応答グラフ」と酷似したものとなりました。
このデータと、最初に設定した各正弦波の振幅（ai）と、次数×ω（niω）を比較してみます。周波数10Hz、40Hz、48Hzで振幅は2と設定していました。 それに対して、上記結果は周波数はおおむね一致しているものの、振幅は若干小さめにでています。 また、周波数20Hzで振幅は5と設定していました。これも前述同様、少し振幅は小さめに出ています。
残念ながら、フーリエ変換したデータが元の関数と完全に一致することはまずありません。 その最大の理由は、Excel等で計算（数値計算）する場合、データが離散化、量子化されているためです。 フーリエ変換で得られたデータは「あくまで近似計算結果である」と、とらえておく必要があります。
