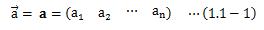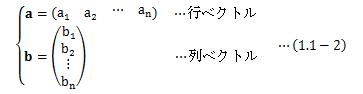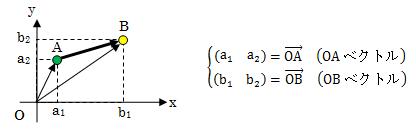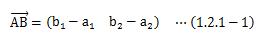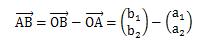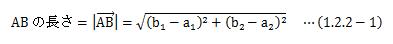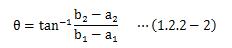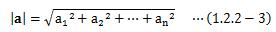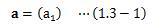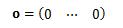1．ベクトルとは？

ベクトルは次のように定義されます。

順序をつけたn個の数の組 （a₁、a₂、・・・、a_n）をn次元ベクトル、
a_kをその第k成分と呼ぶ。このn次元ベクトルは次のように表す。

本サイトではベクトルを太文字aで表すものとします。
この定義を見ると、ベクトルとは 単なる数の組、ということになります。 つまり、高校生のときに習った「大きさと向きを持つ量」という内容はどこにも含まれません。 実はベクトルとは “そんなもん”です。 このベクトルの定義に対して、幾何学的な意味を添えると初めて 「大きさと向きを持つ量」という意味がベクトルに与えられます。 それについては次項で見ていきます。
さて、ベクトルは行でも列でもどちらでも表すことができ、 それぞれを行ベクトル、列ベクトルと呼びます。

ベクトルは行列の仲間であり、行ベクトルは1×n行列、列ベクトルはn×1行列となります。

1．2．ベクトルの幾何学的解釈

まずは、簡単のため2次元ベクトルについて考えます。
2次元直交座標系O－xy上の2点A、Bの位置を（a₁、a₂）、 （b₁、b₂）と置くと、これらは（1.1－1）式より、 （x座標、y座標）を組とする2次元ベクトルになります。

図1.2.1－1　2次元ベクトル

上述のベクトル表記は、基準点（今回はO）を最初に書いて末端点 （今回はA、B）を後に書き、ベクトルを表すために文字の頭に“→” をつけるように定義されます。 今ここで挙げたOAベクトルなどのように、 原点Oから見た位置を表すベクトルを、 位置ベクトルと呼びます。 また、位置ベクトルのように始点が固定されているベクトルを、 束縛ベクトルと呼びます。
今度は原点Oを基準とはせず、始点をA、端点をBとするABベクトルについて見てみます。 （点AB間のx方向の距離、点AB間のy方向の距離）という組が、ベクトルであることをあてはめると、 先ほどの位置ベクトルの考え方を踏襲して、

と表せます。 1.4項で後述しますが、 これは結局のところ以下のようなベクトルに分解できます。

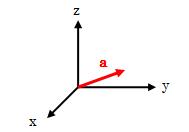
これまで見てきた2次元ベクトルは、常に一つの平面内に存在することから、 平面ベクトルといいます。 それに対し、1次元追加した3次元ベクトルは、 常に一つの空間内に存在することから、空間ベクトルといいます。

図1.2.1－2　3次元空間ベクトル

1．2．2．ベクトルの大きさと向き

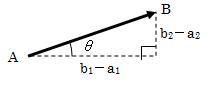
次に、ABベクトルの長さについて考えます。

上図1.2.2－1からもわかるように、ABベクトルの長さは簡単に求められます。

ベクトルの大きさを表す場合、ベクトルの絶対値として表現します。 また、座標系の2成分が決まっていることから、ABベクトルの方向も次のように決めることが出来ます。

よって、ベクトルとは幾何学的に見れば 「大きさと向きを持つ量」であることがわかります。
さて、二次元ベクトルの長さ＝大きさを（1.2.2－1）式で求めましたが、 この考え方は次元数を大きくしても同じように適用されます。 つまり、n次元ベクトルの大きさは次のように表すことが出来ます。

このベクトルの大きさはノルムとも呼びます。

1．2．3．ベクトルと有向線分

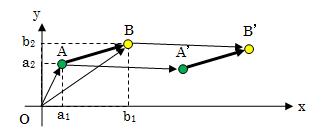
ここで一つ注意点があります。 結論から言うと、ベクトルと有向線分は違うということです。 以下に、その違いについて見ていきます。
まずは有向線分の定義について見てみます。 “線分”とは長さが有限の直線のことです。 その頭に“有向”とつくことから、有向線分は 向きを持つ線分ということになります。 これだけを見るとベクトルと同じように思えます。 そこで、下図のように、点A、Bが同じ方向に同じ量だけ移動（平行移動）した場合を考えます。

有向線分ABとA'B'は当然同じ大きさ、同じ向きになります。ただし、線分が存在する位置がちがうため、 “有向線分AB≠有向線分A'B'”になります。
それに対し、ベクトルでは“ベクトルAB＝ベクトルA'B'”として扱います。 それは、ベクトルABとベクトルA'B'を成分表示するとまったく同じになるからです。 つまり、ベクトルと有向線分は同じではないことになります。 ベクトルは、大きさと向きが同じ有向線分（位置が違っても良い）を、すべて同じものとして扱います。

＊）単なる数の組を数ベクトル、有向線分によって表すベクトルを 幾何ベクトルと区別することがあります。

1．3．ベクトルとスカラー

ベクトルとは前述のとおり、大きさと方向を表す量になります。 そしてベクトルの表現は、（1.1－1）式のように次元数分の成分を持った数の組で表されます。

それに対し、大きさだけで表す量をスカラーと呼びます。 大きさしか表しませんからスカラーの次元は1次元になります。 （1.1－1）式を1次元表記すると、一次元ベクトルとして次のように表せます。

こう書くと何か深い意味があるように見えますが、何のことはなく 「スカラーとはただ単なる数」です。 ベクトルとスカラーの決定的な違いは、座標系によってその値が変化するかどうか？です （手っ取り早く見るには行列式を掛けてみるのが良いでしょう）。 ベクトルは座標系によってとる値は変化しますが、スカラーは変化しません。
ここで、ベクトルとスカラーの具体的な物理量の例について見てみます。 ベクトルとは大きさと方向を持つ量ですから、次のようなものが挙げられます。

速度、加速度、力、運動量、電場、磁場・・・

それに対し、スカラーは大きさのみを持つ量ですから、次のようなものが挙げられます。

質量、温度、摩擦係数、エネルギー、電荷量、抵抗、光速・・・

1．4．ベクトルの演算法則

ベクトルは、以下に示す演算法則が定義されています。

ここで、重要なベクトルを定義しておきます。

（a）零ベクトル

（b）単位ベクトル

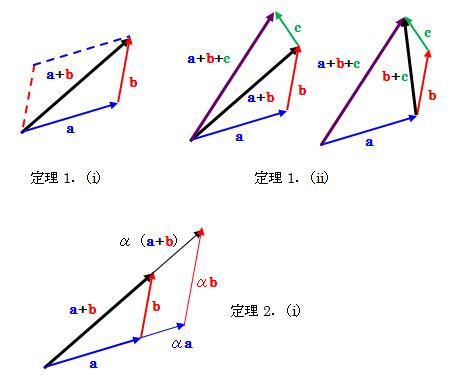
前述の演算法則（1）～（3）に従い、次の定理が成り立ちます。 二つのベクトルa、b、 スカラーα、βとします。

これらを幾何学的に見ると、次のような図になります。

（定理2（ii）、（iii）は省略） また、成分がすべて実数のみのベクトルを実ベクトル、 複素数を含むベクトルを複素ベクトルとよび、 上記定理はどちらでも成り立ちます。

参考文献

関連ページ