1．数の概念

“数”の起源は、「数える」という行為から生まれたものと考えられています。 この「数える」という行為には、次のようなものがあります。

• 獲物を何匹とったか？＝“個数（量）”を表す
• 誰が一番狩りがうまいか？＝“順番”を表す

“数”の概念がうまれたことで「獲物をどれだけあるか？」（=個数）とか「狩りがどれだけうまいか？」（=順番）を具体的に表現できるようになりました。 さらに“数”という道具を手に入れたことで、重さや長さなどの表現方法をつくって、個数でしか表せなかった量を別の形で、しかもかなり細かく表現できるようになりました。 こうして“数”の概念が発展すると共に、人間の表現方法も豊かになっていった、と考えられます。 つまり、“数”とはコミュニケーションの道具＝言葉そのものである、といえます。 1、2、3、・・・という形で表現されていた“数”は現在、小数、分数、複素数などたくさんの“数”が生み出され、その表現力が増しています。 表現力が増したことで“数”の概念は複雑化するとともに様々な性質・特徴を持つようになりました。 人間はその特徴に応じて“数”を分類しています。 （分類こそが人間の知性の源であると思っています）。 そこで本ページでは、様々な種類の数について見ていくことにします。

2．数の表現

“数”は無数にあり、それらはさまざまな形で表現されます。 そこで、本章では、数の表現方法について説明します。

整数、小数、分数、平方根（三乗根・・・）、虚数

2．1．整数

1、2、3・・・等のきりの良い数を“整数”といいます。 後述(3章)しますが、この整数の中で、 1より大きい整数を自然数と呼び、0や負の数も含めたものを整数といいます。

2 ．2．小数

小数とは、0と1、1と2、2と3…という、となりあう整数の間にある一の位より小さい数を表します。 具体的に言うと次のようになります。 まず、0と1の間を10等分します。

図2.2－1　小数を表す数直線

このとき、0と1のちょうど中間の数字をどのように表すか？について考えます。 0と1を10等分したちょうど真ん中は上図の5個めの目盛りになります。 ただ、この目盛りを整数だけで表すことは出来ません。 そこで、

“1番目の目盛りの値”＝“1を10で割った値”＝“0.1”

と呼ぶことにしました。

“0.1”について詳しく見ていきます。
最初の“0”は位を表すためにただ単に用いられている数字、と考えます。 “0”の後ろにある点“．”は、整数では表せない1より小さい数値を表す区切りを表すもの、と考えます。 この点を小数点と呼びます。 “．”の後ろにある数字は、0と1を10個に区切ったとき、何番目に相当するか？を表すものです。
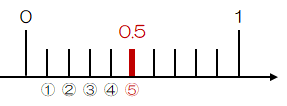
そうすると、0と1のちょうど中間の数字は5番目の目盛りになりますので“0.5”と表すのが妥当だと考えられます。

図2.2－2　小数を表す数直線

同じように考えて、0と0.1の間にある数字は0.0Xで、0と0.01の間にある数字は0.00Xで表します。
最後に、小数は次の3つに区分けされます

有限小数	：	0.5や0.8215など小数点以下の数字に限りの有る小数です。
無限小数	：	3.141592…（円周率）などのように、小数点以下の数字が限りなく続く小数です。
循環小数	：	無限小数のうち、0.1333…=0.13（1/3）や0.34545…=0.345（19/55）のように限りなく同じ数字が繰り返される小数です。

2 ．3．分数

分数は、ある数字を別の数字で割ることを表現した数です。 つまり割り算を数字として表現しているだけです。 例えば、リンゴを半分に切ったときの量1÷2＝1/2（=0.5）、サイコロで1が出る確率1÷6＝1/6（=0.1666・・・）、8個のまんじゅうを4人に配ったときに各人がもらえる個数8÷4＝8/4（=2）などがあります。 分数は、整数を表すこともあれば、小数を表すこともあります。 ただし、小数で表せる分数は、必ず有限小数か循環小数になります。

2 ．4．平方根

同じ数を2個掛け合わせることを二乗といいます。 つまり2×2＝2²＝4です。 平方とはこの二乗を意味します。 その根（もと）となる数（前例で言えば“2”）を平方根と呼びます。 例えば、平方根をXとおき、以下の式が成り立っているときのXの値を次のように表現します。
\[ 2 = X \rightarrow \ X = \sqrt{2} \] ちなみに平方根は二乗のときの呼び方ですが、三乗根、四乗根・・・などを含めた総称を“べき乗根”と呼びます。

2．5．虚数

虚数とは、-1の平方根として定義されています。
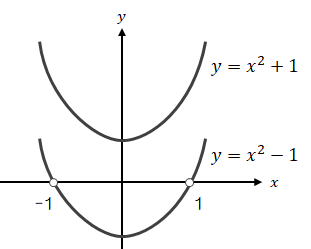
また、\( \alpha i \)（\( \alpha \)は実数）と表せる数を純虚数と呼びます。 なぜ“虚”数と呼ぶのでしょう？ “虚”を辞書で調べると“実”の反対語と記されています。 また、英語での虚数はimaginaryと言います（この頭文字は“i”）。 この単語の意味は、「創造上の、架空の、空想の」などといった意味です。 これは以下の図をみると直感的に理解できると思います。

xy平面上に二つの曲線があります。一つはx軸と交わる曲線（ \( y = x^2 - 1 \) ) もう一つはx軸と交わらない曲線（ \( y = x^2 + 1 \) ）とします。 両曲線について、\( y = 0 \)となる場合\( x \)の値はどのようになるかを考えます。 x軸と交わる曲線（ \( y = x^2 - 1 \)）は\( y = 0 \)のとき、上図の通り\( x = \pm 1 \)で交わるので、それが答えになります。 ではx軸と交わらない曲線（ \( y = x^2 + 1 \) ）のときはどうでしょう？x軸と交わりませんので、上図から判断する場合、 答えは“なし”となってしまいます。 しかしながら数式上は、次のように表現することが可能です。
つまり、人間が実感できる（と書けばよいでしょうか？）世界においてこの数は答えにはなりませんが、数学またはそれを基にした学問においては数として扱いましょう、 \( i \)は架空の数字としてとらえましょう、ということから虚数（imaginary）という名称がついたと考えられます。 虚数は、物理学（電磁気学、量子力学、振動現象、連続体力学など）の理論構築において重要な役割を担っています。 また、実用上でも虚数を用いることで煩雑な計算を簡素化することが可能になります（例えばフーリエ変換など）。 また、面白い例えとして「ガモフの問題（＝宝探しゲーム）」というものがあります。 この詳細については、以下の書物をご覧いただければと思います。

そのほか、別の虚数として四元数（クォータニオン）があります。 この虚数はロボットアームや人工衛星の姿勢制御、素粒子物理等で出てきますが、 少し特殊ですのでここでは説明を割愛します。

参考文献

関連ページ