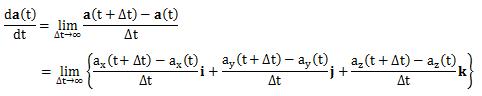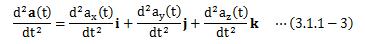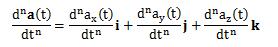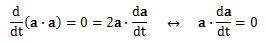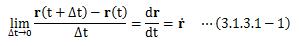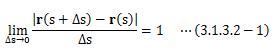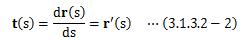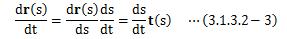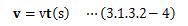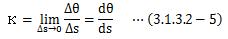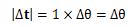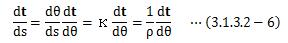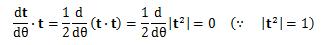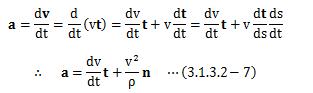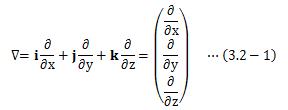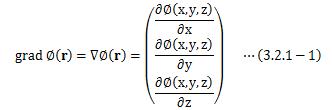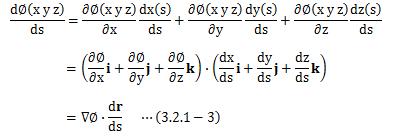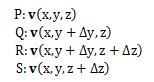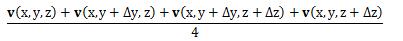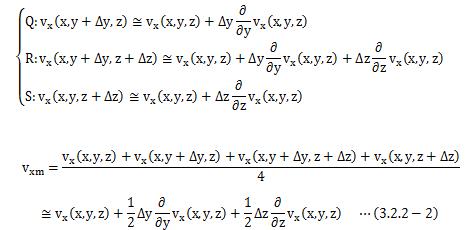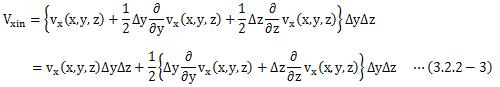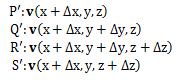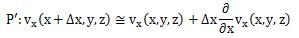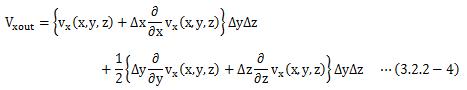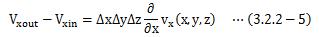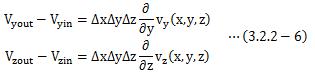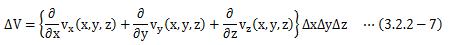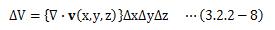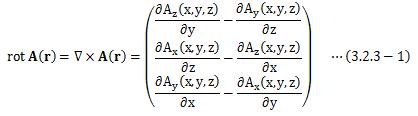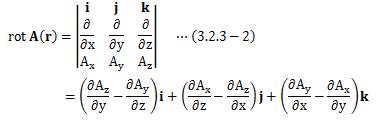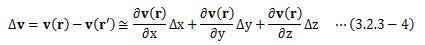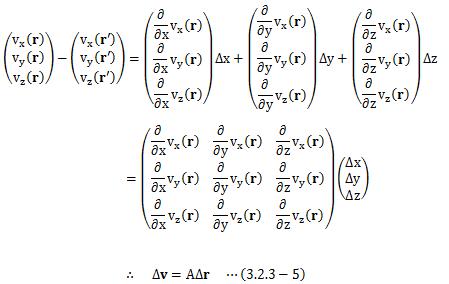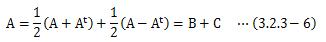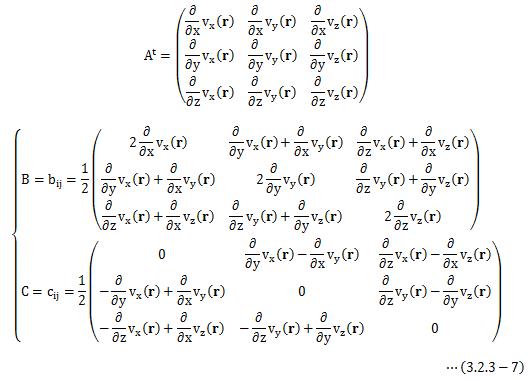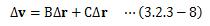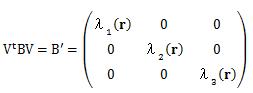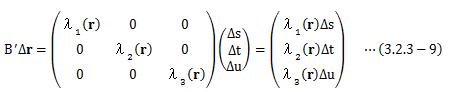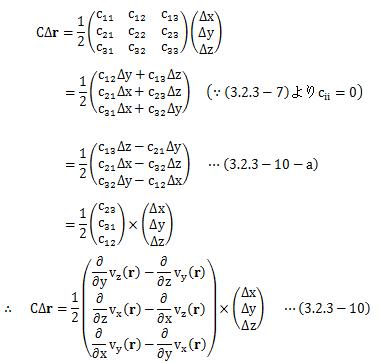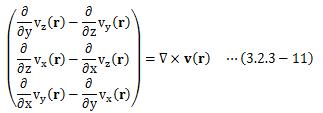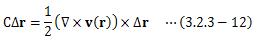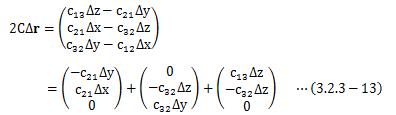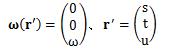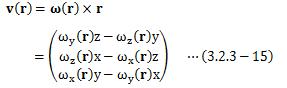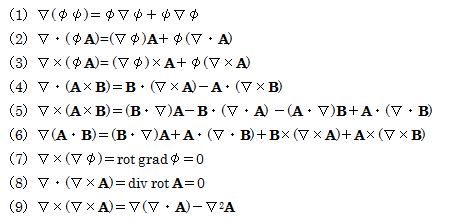ベクトル解析
3.ベクトル解析
本章では、3次元空間上のベクトルに微分法を適用していきます。 この空間に存在する正規直交座標系O-xyzについて、 x、y、zの各軸方向を表す単位ベクトルを i、j、kとします。3.1.ベクトルの微分
3.1.1.ベクトル微分の定義
空間ベクトルaがある変数、ここではtとしたときの関数である場合、 それをベクトル関数a(t)と呼びます。 ベクトル関数の成分を以下のように設定します。さて、ベクトル関数a(t)をtで微分すると、
ベクトルi、j、kは定ベクトルなので、
となります。 同様に2階微分の場合は次のようになります。
(3.1.1-3)式を発展させれば、結局のところ、空間ベクトルの高階微分は、
となります。
3.1.2.ベクトル微分の演算法則
スカラー関数k(t)、ベクトル関数a(t)、 b(t)の間には次の関係式が成り立ちます。上式は成分計算をすることによってすべて証明できます。 特に(2)について、b(t)=a(t)=a (定ベクトル)の場合、
が成り立つので、ベクトルaと その1階微分da/dtは必ず垂直になります。
3.1.3.曲線に関するベクトル
3.1.3.1.接線ベクトル
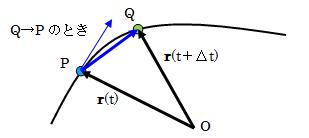
今、三次元空間上に曲線Cが存在するとします。 この曲線C上を動く質点の運動について考えて見ます。図3.1.3.1-1 曲線C上の質点の動き
質点がある時刻tで、曲線C上の点Pにあるものとし、その位置ベクトルをr(t)とします。 それから微小時間Δt経過後、質点が曲線C上の点Qに移動したとします。 この点Qの位置ベクトルをr(t+Δt)とし、 PQベクトルをΔr=r(t+Δt)-r(t)とします。 ここで、Δtを十分小さくすると、点Qは点Pに近づいていき、Δt→0の極限において、 Δrの向きは点Pにおける接線方向と一致します。
このベクトルdr/dtを、点Pにおける曲線Cの接線ベクトルと呼びます。 ちなみに速度ベクトルは、位置ベクトルの時間微分であることから、 この接線ベクトルはまさに速度ベクトルと同じものになります。 つまり表現を変えると、dr/dtは点Pにおける質点の速度ベクトルである、とも言えます。
3.1.3.2.主法線ベクトル
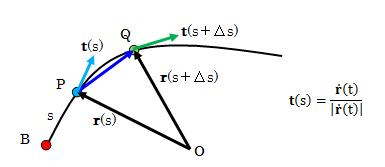
先ほどは、質点の位置を時間tを変数とするベクトル関数として表現しましたが、 今度は、曲線上のある1点Bを基準に、そこから測った弧BPの長さsをパラメータとして、 質点の位置をベクトル関数r(s)で表すことにします。 3.1.3.1項の接線ベクトルについて、 その大きさが1である単位接線ベクトルをt(s)と置きます。図3.1.3.2-1 曲線C上の質点の動き
図3.1.3.2-1のように、点Pから微小距離Δsずれた点をQとし、 その位置ベクトルをr(s+Δs)、 PQベクトルをΔr=r(s+Δs)-r(s)とします。 ここで、Δsを十分小さくすると、点Qは点Pに近づいていき、 Δs→0の極限において、Δrの大きさはΔsと一致します。
また、Δrの向きは点Pの接線と一致します。 つまりΔs→0の極限において、dr(s)/dsは点Pでの単位接線ベクトルを表します。
ここで、(3.1.3.1-1)と(3.1.3.2-2)式の結果、 さらに合成関数の微分則を用いて次のような関係が導き出せます。
上式のスカラー微分ds/dtは、距離の時間変化を意味しています。これはまさに速さを表しています。 よって、速さをv、速度をvとすると、上式は次のように表せます。
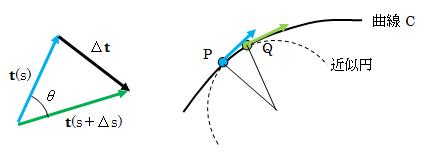
今度は、単位接線ベクトルの距離sによる変化について考えて見ます。 図3.1.3.2-1において、ベクトルt(s)とt(s+Δs)の成す角をΔθと置きます。
図3.1.3.2-2 曲線Cの曲率
点Qが点Pに十分近いとき、上図3.1.3.2-2のように、 点Pで曲線Cに接する円周上に2点P、Qが存在する、と考えられます。 そこで、次のようなパラメータを新たに設定します。
これは、微小角度dθに対する半径1の円弧長dθと、 曲線Cの弧長dsの比を表すもので、曲率と呼びます。 この定義からわかるように、曲率は曲がり具合を表すパラメータです。 “曲率が大きい”とは、Δθ>Δsですから半径1の円よりも曲線Cの弧長が短い、 ということですから曲がり具合がきついことを意味します。
図3.1.3.2-3 曲率の大きさ例
また、曲率кの逆数を曲率半径ρと呼びます。 これは曲率の定義からすんなりと受け入れられると思います。 さて、Δθが十分小さいとき、Δtの大きさは、t(s)が単位接線ベクトルであることから
となりますので、次の関係が成り立ちます。
つまり、dt/dθは単位ベクトルになります。 次に、dt/dsを合成関数の微分則を用いて以下のように変形します。
単位接線ベクトルtとdt/dθの幾何学的関係は、 その内積をとるとわかるように、直交しています。
dt/dθが接線に垂直なベクトルということは、 接線に接する円の中心に向かうベクトルということになります。 まとめると、このdt/dθは大きさ1、 接線に対し垂直な方向=曲率円の向心方向を持つベクトルで、 主法線ベクトルと呼び、nで表します。
ここで、主法線ベクトルを用いた形での加速度ベクトルを求めてみます。
(3.1.3.2-4)、(3.1.3.2-6)式を考慮にいれて、 となります。 この式から加速度ベクトルは、速さの変化を表す接線方向と、 方向変化を表す向心方向の2方向成分で構成されていることがわかります。
3.2.場と微分演算子
3次元空間上の任意の点の位置ベクトルをr=(x、y、z)としたとき、 各点にベクトル関数A(r) =(Ax(r)、Ay(r)、Az(r))が 与えられるとき、その空間をベクトル場と呼びます。 例えば、電場や磁場、重力場、速度場などがベクトル場に相当します。それに対し、各点にスカラー関数φ(r)が与えられるとき、 その空間をスカラー場と呼びます。 例えば、等電位面やポテンシャル流などがスカラー関数として与えられるときが、 スカラー場に相当します。
“場”という概念で、ベクトル関数、あるいはスカラー関数である物理量を考えるとき、 各点に与えられたベクトル関数の変化を知ること、 つまりベクトル関数の位置ベクトルrに関する微分が、 現象を把握する上で非常に重要になります。 そこで、次のような微分演算子を定義します。
この(3.2-1)式の演算子∇を、ナブラ演算子と呼びます。 この演算子は、ベクトル関数のx成分をxで、y成分をyで、 z成分をzによって偏微分することを表しています。
さて、この微分演算子によって以下の4種類の計算則が定義されています。
3.2.1.勾配(grad)
スカラー関数φ(r)の場における変化は、 勾配(gradient)として次のように定義されます。(3.2.1-1)式がなぜ“勾配”と呼ぶか?について調べてみます。
スカラー関数φ(r)は、曲線C上の点として定義されているものとします。 C上のある1点Bを基準に、そこからC上のある点Pまでの曲線長をsとします。 今、点Pの位置ベクトルをrとしたとき、点Pをつぎのように表します。
ここで、関数φ(r)=φ(x(s)、y(s)、z(s))の曲線長sによる変化を計算すると、
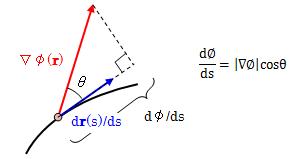
となります。 (3.2.1-3)式左辺のdφ(r)/dsを方向微分係数と呼びます。 また、(3.2.1-3)式右辺のdr(s)/dsは、 3.1.3.2項の (3.1.3.2-2)式で見たように、曲線Cの単位接線ベクトルを表します。 よって、(3.2.1-3)式は∇φ(r)と接線ベクトルとの成す角をθとして、次のようになります。
図3.2.1-1 方向微分係数
θ=0のとき、dφ(r)/dsは最大値|∇φ(r)| をとります。 つまり∇φ(r)は、φ(r)が最も急激に変化する方向を向きます。
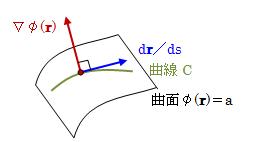
次に、φ(r)=a(定数)とすれば、 この式は3次元曲面を表します。この曲面をSとします。 この曲面S上に曲線Cをとれば、曲線C上の点Pはφ(r)=aによって拘束されます。 さて、曲線Cをパラメータsによって表すとき、曲線状の点Pは(3.2.1-2)式で表せます。
そこで、(3.2.1-3)式同様、パラメータtによる関数φ(r)の変化を計算すると、 φ(r)は一定のため、
つまり、∇φと曲線Cの接線ベクトルは垂直であることがわかります。 ところで、この曲線Cは、曲面S上と定義しただけですので任意性を有します。 そのため(3.2.1-4)式は、点Pにおける任意の曲線Cに対して成立します。 言い換えれば、(3.2.1-4)式は曲面Sに対して成立します。 つまり、∇φ(r)=constのとき、∇φ(r)と曲面Sは垂直である ことがわかります。 また、このときの曲面Sを等位面と呼びます。
図3.2.1-2 等位面とgradの関係
3.2.2.発散(div)
ベクトル関数A(r)の場における変化は、 発散(divergence)として次のように定義されます。(3.2.2-1)式がなぜ“発散”と呼ぶか?について、具体的な例で調べてみます。
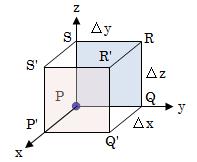
下図3.2.2-1に示す、辺の長さがΔx、Δy、Δzとなる 微小直方体領域から流出する流体の体積について考えます。 流体のある点P(x、y、z)における速度をv(x、y、z)とします。
図3.2.2-1 流体の発散
図3.2.2-1の、x軸に垂直な青色の面PQRSから直方体に流入する、 単位時間あたりの流体の体積は、次のように計算できます。
青色面PQRSの面積×その面を通過する流体の速度
そこで、青色面PQRSを通過する流体の速度を求めます。 青色面PQRSの4頂点の速度は次のようになります。
青色面PQRSは微小面積のため、この面を通過する流体の速度は、 PQRS4点の平均として考えると、
となります。 ところで今、青色面からの流入体積を求めようとしているので、 この面の平均速度はx軸成分のみを考えればよいことになります。 また、Δy、Δzは微小量のため、テイラー展開して2次以上の項を無視すると、
よって、青色面PQRSから直方体に流入する単位時間あたりの流体の体積は、
今度は、赤色面P'Q'R'S'から流出する単位時間あたりの流体の体積を求めます。 (赤色面P'Q'R'S'の頂点の速度は次のようになります。
先ほどの流入してくる計算と同じように計算しますが、 今回は微小量にΔxが追加されます。 よって、まずは点P'の速度についてテイラー展開し、 2次以上の項を無視すると、
となります。 この式を他の点にも用いて、赤色面P'Q'R'S'から直方体に出て行く単位時間あたりの流体の体積を計算すると、
となります。 最後に、x軸方向における流体の流出量は、流出量(3.2.2-4)から流入量(3.2.2-3)式を引くことによって求まります。
残りのy軸、z軸も同様に計算すれば、それぞれ
よって、直方体の表面を通って、単位時間あたりに流出する流体の体積は、 (3.2.2-5)と(3.2.2-6)を足し合わせればよく、
となります。 この(3.2.2-7)式を、(3.2.2-1)式と比較すると、次のように表すことが出来ます。
このように、ある領域からの流出量を計算する際にdivが用いられる ことから、発散と定義されるのはごくごく自然なことと考えられます。
3.2.3.回転(rot)
ベクトル関数A(r)の 回転(rotation)は、次のように定義されます。また、行列式を用いると、
となります。
(3.2.3-1)式がなぜ“回転”と呼ぶか?について、具体的な例で調べてみます。
ベクトル場のある点P(x、y、z)(点Pの位置ベクトルr) における速度ベクトルをv(r)=v(x、y、z)とします。 ここで、点P近傍の点Q(x'、y'、z')=r'について考えます。 点Pと点Qは近傍であることから、r'-r =Δr=(Δx、Δy、Δz)の大きさは微小になります。 さて、点Qでの速度ベクトルはv(r') =r(x'、y'、z')と表せますので、 点Qにおける速度ベクトルv(r)のテイラー展開を求め、 2次以降は微小として無視すると、
と表せます。 (3.2.3-3)式は、ちょっと書き換えるとわかりますが、 点Pと点Qの間の速度ベクトル変化を表しています。
この速度ベクトル変化の中身を知るために、(3.2.3-4)式を面倒くさいですが成分表示してみます。
ここで、任意のn次正方行列Aは、n次対称行列Bとn次反対称行列(交代行列)Bの和で表すことが出来ます。
これを、(3.2.3-5)式の行列Aに適用して行列B、Cを求めると次のようになります。
(3.2.3-5)式を、行列B、Cを用いて書き直せば、
となります。 ここで、BΔrと、CΔrが持つ幾何学的な意味について考えて見ます。 まずは、BΔrから見ていきます。 行列Bは対称行列のため、固有ベクトルから得られる直交行列Vによって対角化可能です。 求める対角行列をB'としたとき、行列の対角化は
で表すことが出来ます。 また、直交行列Vによって位置ベクトルΔrは、座標変換され、 そのベクトルをΔr'=(Δs、Δt、Δu)と置きます。 この対角化された行列B'による、座標変換された位置ベクトルΔr' の変換は次のように表せます。
これは、x、y、zの各成分はそれぞれのスカラー倍、という関係になっていますので、 B'による速度ベクトルの変化は、伸縮を表します。
次に、CΔrについて見ていきます。
と、ベクトルの外積の式に書き換えることが出来ます。 ここで、外積の第一項を、rotの定義式である(3.2.3-1)式と比較すると、
であることがわかります。 よって、(3.2.3-10)式は次のように書き換えられます。
さて、ここで(3.2.3-10-a)式を次のように書き換えます。
このように書くと、右辺第一項のベクトルはxy平面上の点、右辺第二項のベクトルはyz平面上の点、 右辺第三項のベクトルはzx平面上の点を表すことがわかります。 これら三つのベクトルは同形のため、一つのベクトルの特徴をつかめばよいことになります。 よって、xy平面上の点を表す右辺第一項のベクトルについて着目します。 右辺第一項のベクトルは、次のように書き換えられます
ここで、再度(3.2.3-8)式を見直すと、
今求めようとしているのは、空間上の点間における速度差ベクトルで、 そのうちの行列C寄与分です。この速度差ベクトルの行列C寄与分を vcと置きます。 そこでこのvcをxy平面に射影したベクトルvcxyが、 仮にc12=constの場合、xy平面上でどのように分布するか?について考えて見ます。
q=(Δx、Δy、0)とおき、|q|=constを満たす点の vcxyがどのようになるか?を具体的に計算して図示化すると、 下図のようになります。
図3.2.3-1 xy平面状のvcxyの分布
つまりvcxyは、原点(この場合z軸)を中心として、 時計まわりの回転を示しています。 同様にすると、他のyz平面、zx平面についても同じことが言えます。 よって、vcは回転を表すことがわかります。 (3.2.3-13)式に再度登場してもらうと、
行列Cと1/2 (∇×v(r))×は等価であることがわかります。 つまり、∇×v(r)は回転を表していることが、これではっきりしました。
また、力学上定義されている回転運動の式を以下に示します。
ω(r)は角速度ベクトルです。 ここで、角速度ベクトルω(r)を、正規直交座標系のz軸と一致するように座標変換したときの、 角速度ベクトルと位置ベクトルを次のように表します。
そのとき、(3.2.3-14)式を(3.2.3-1)式に代入すると、
となります。 先ほどの結論で、行列Cと1/2 (∇×v(r))は等価であることがわかりましたので、 行列Cは角速度ベクトルω(r)と等価であることがわかります。