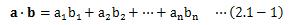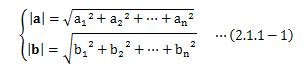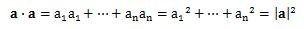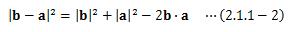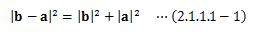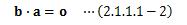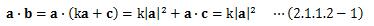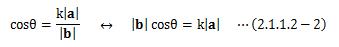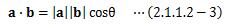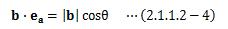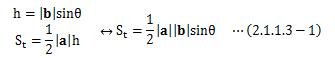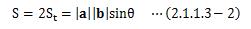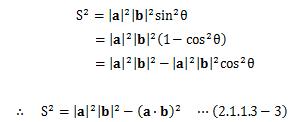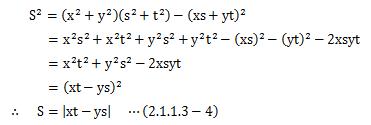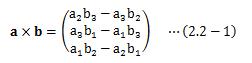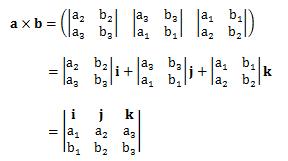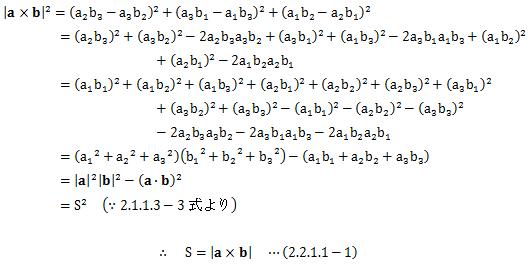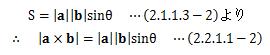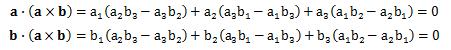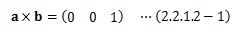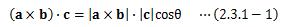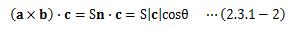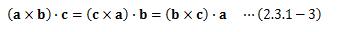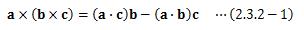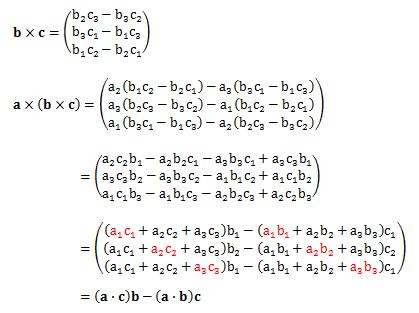2．ベクトルの積

2．1．内積（スカラー積）

二つのn次元ベクトルa、bの内積は、 次のように定義されています。

行列計算として書けば、

となります。

2．1．1．内積の幾何学的意味

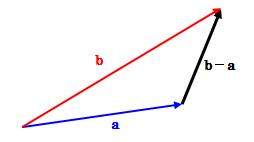
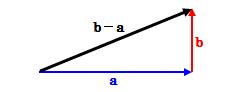
ここでは内積の幾何学的意味について見ていきます。 下図のような三角形のそれぞれの辺の長さについて考えます。

図2.1.1－1　内積について

ベクトルa、bの長さは（1.2.2－1）式により

と表せます。 ところで、同一ベクトルの内積を計算してみると

になることがわかります。 つまり、同一ベクトルの内積は、ベクトルの大きさの二乗になります。
次にベクトルb－aの長さを求めてみます。

ここから内積の重要な性質を導き出していきます。

2．1．1．1．内積の直交性

ベクトルa、bが直角の場合を考えます。

図2.1.1.1－1　直交ベクトルの内積

このとき、ピタゴラスの定理から次の関係が成り立ちます。

（2.1.1－2）式と比べると、

となることがわかります。 つまり、零ベクトルでない二つのベクトルa、bが直交するとき、 その内積a・b＝0になります。

2．1．1．2．ベクトルの射影

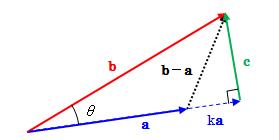
図2.1.1.2－1　内積の射影

上図のようにある実数kをとり、ベクトルaをk倍したベクトルkaと、 ベクトルbによって作られる三角形（最後の一辺をベクトルc）が 直角三角形であるとします。 するとaとbの内積は、 aとcが直角なので、

となります。 ここで三角形の余弦定理から、

（2.1.1.2－1）、（2.1.1.2－2）式からkを消去すると、

となります。 これにより、二つのベクトルが成す角度θを決めることが出来ます。
また、ベクトルaの方向を指す単位ベクトルをe_aとすれば、（2.1.1.2－3）式は次のように書き換えられます。

この式は、ベクトルbを ベクトルaの方向に射影したときの大きさを 表すことになります。

2．1．1．3．平行四辺形の面積

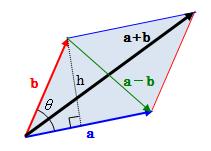
ここでは、ベクトルの内積から行列式の幾何学的意味について導き出します。

図2.1.1.3－1　平行四辺形の面積

ベクトルa、b、 a－bで囲まれた三角形の面積は次のように表せます。

平行四辺形の面積は、上記三角形の面積二つ分になりますので、

となります。 ここでθを消去するため（2.1.1.3－2）式を両辺二乗して、内積の定義を代入すると、

ところで、a＝（x、y）、b＝（s、t）とすると、 （2.1.1.3－3）式は、

さて、この式は次の行列の行列式になっていることがわかります。

つまり、行列式の幾何学的意味は、平行四辺形の面積を表します。 このように内積の計算から、行列式の幾何学的意味を導き出すことが出来ます。

2．1．2．内積の演算法則

内積は、以下に示す演算法則が成り立ちます。

1. 交換則

   a・b＝b・a　（a、b：実ベクトル）

2. 分配則

   （a＋b）・c＝a・c＋b・c

3. スカラー乗法

   （αa）・b＝a・（αb）＝αa・b　（α：実数）

4. シュバルツの不等式

   |a・b|≦|a|・|b|

2．2．外積（ベクトル積）

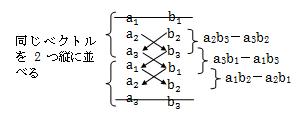
二つの3次元ベクトルa、bの外積は次のように表します。

この計算の中身は次のようなものになります。

また、下記の計算方法が覚えやすいかもしれません。

さて、内積の計算結果はスカラーであったのに対して、 外積の計算結果はベクトルになります。

2．2．1．外積の幾何学的意味

2．2．1．1．外積の大きさ

まずは、外積の大きさについて見てみます。 3次元ベクトルa＝（a₁、a₂、a₃）、 b＝（b₁、b₂、b₃）の外積について、地道に成分計算していきます。

このように外積の大きさは、2つの3次元ベクトルa、 bによって作られる平行四辺形の面積を表します。 また、外積の大きさの別の表現として、（2.1.1.3－2）式から

と表せます。 ところで、内積は

で表せることから、内積と外積の大きさはcosθとsinθを入れ替えただけ の違いであることがわかります。

2．2．1．2．外積の向き

次に外積の向きについて見てみます。 a×bとベクトルa、 ベクトルbの内積を計算すると、

つまり、a×bとa、 bは直交していることがわかります。 このとき、aとbに垂直な方向は2種類あります。 例えて言うなら（0、0、1）と（0、0、－1）といったようなことです。 そこで、正規直交座標系で考えてみると、a＝（1、0、0）、 b＝（0、1、0）とすれば、

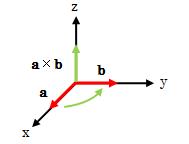
となります。 これを図に表したのが図2.2.1.2－1になります。

図2.2.1.2－1　外積ベクトルの方向

外積a×bの方向は、 外積の最初のベクトルaをベクトルbへ回したとき、 右ねじの進む方向と一致することになります。

2．2．2．外積の演算法則

外積は、以下に示す演算法則が成り立ちます。

1. 反交換則

   a×b＝－b×a

2. スカラー乗法

   （αa）×b ＝α（a×b） ＝a×（αb）

3. 分配則

   （a＋b）×c ＝a×c＋b×c

2．3．三重積

ベクトルの三重積には次の2種類があります。

1. スカラー三重積

   （a×b）・c

2. ベクトル三重積

   （a×b）×c

2．3．1．スカラー三重積

スカラー三重積は次のように計算できます。

上式は外積ベクトルa×bをベクトルcの方向へ射影し、 それぞれのベクトルの大きさを掛け合わせたものになります。
さて、外積ベクトルa×bは ベクトルa、bによって作られる平行四辺形を含む平面に垂直です。 この平面に対して垂直で大きさ1のベクトル のことを法線ベクトルと呼びます。

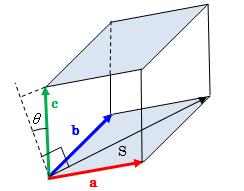
と表せます。 これは、下図2.3.1－1のような平行六面体を考えたとき、底面積S、 高さ|c|cosθによって求められる体積を表していることがわかります。 つまり、スカラー三重積は平行六面体の体積を表すことがわかります。

図2.3.1－1　スカラー三重積の意味（平行六面体の体積）

ただし、cos項は正負両方とりますので、体積に対して符号がつくことになります。
最後に、スカラー三重積はベクトルの順序を循環的に変えてもその値は変わりません。

2．3．2．ベクトル三重積

ベクトル三重積は、スカラー三重積のような幾何学的な意味は特にありません。 ベクトル三重積は次のように変形できます。

これは、次のように地道に成分計算することで導き出せます。

一般に、a×（b×c） ≠（a×b）×cになります。

参考文献

関連ページ