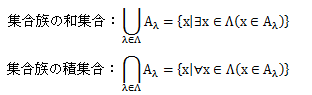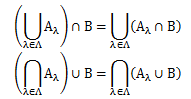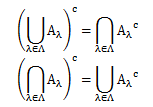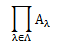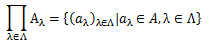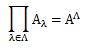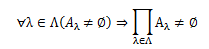3．4．写像の演算

3．4．1．集合の像と逆像

fを集合AからBへの写像とします。 Aの任意の部分集合Xに対し、その元xのfによる像f(x)をすべて集めてできる集合を、fによるXの像といいf(X)で表します。 f(X)はBの部分集合であることは明らかです（図3.4.1－1左側参照）。 次に、YをBの任意の部分集合としたとき、f(x)∈YとなるAの元x全てを集めてできる集合を、 fによるYの逆像または原像と呼びf^-1(Y)で表します。 f^-1(Y)もまたAの部分集合であることは明らかです（図3.4.1－1右側参照）。

図3.4.1－1　像と逆像

以上の定義から、以下のことが言えます。

• （1）∀a∈Aに対し、f(a)∈Bゆえf^-1(B)=A（∵A=(fの定義域)）
• （2）Y≠φであっても、f^-1(Y)=φはあり得る（∵B⊃(fの値域)）
• （3）f(X)=φ　⇔　X=φ

また、次の演算則を定理として挙げることが出来ます。 ただし、P、P₁、P₂⊂A、Q、Q₁、Q₂⊂Bとします。

1. P₁⊂P₂　⇒　f(P₁)⊂f(P₂)
2. f(P₁∪P₂)＝f(P₁)∪f(P₂)
3. f(P₁∩P₂) ⊂f(P₁)∩f(P₂)
4. f(A－P)⊃f(A)－f(P)
5. Q₁⊂Q₂　⇒　f^-1 (Q₁)⊂f^-1 (Q₂)
6. f^-1 (Q₁∪Q₂)＝f^-1 (Q₁)∪f^-1 (Q₂)
7. f^-1 (Q₁∩Q₂)＝f^-1 (Q₁)∩f^-1 (Q₂)
8. f^-1 (B－Q)＝A－f^-1 (Q)
9. f^-1 (f(P))⊃P
10. f^-1 (f(Q))⊂Q

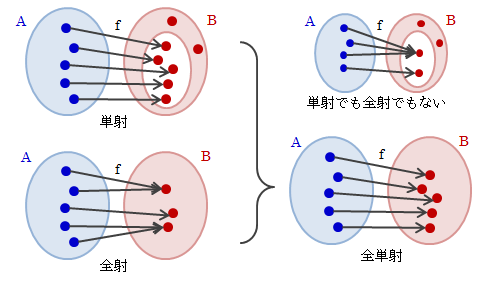
3．4．2．単射・全射・全単射

単射、全射、全単射は、写像において非常に重要な概念になります 集合AからBの写像をfとし、その値域をV(f)とします （写像の定義により始集合Aと定義域D(f)は一致します）。 このとき、写像の形として次のようなもの分けられます。

図3.4.2－1　単射・全射・全単射

（1）単射

（2）全射

（3）全単射

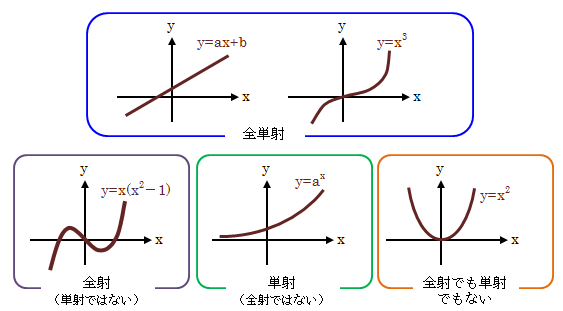
この定義に基づき、単射、全射、全単射の関数例を以下のグラフに示します。

図3.4.3－2　全射・単射の例

3．4．3．逆写像

写像fの像はf(A)であり、この逆像はf^-1(B)となります 今、Y→f^-1(B)とする対応f^-1が写像となる条件について考えてみます。
写像の条件は次の2つです。

1. 始集合のすべての元に対し、終集合のただ1つの元が決まる
2. 始集合と定義域は一致

今回の場合、始集合はA、終集合はBとなります。 fが写像であることと、条件（1）（2）から次のことが言えます。 f^-1を写像と仮定すると、fによってAのすべての元がBに写され、f^-1によってBのすべての元がAに写されます。 ここで、B’=B－f(A)（≠φ∧⊂B）とすれば、その逆像f^-1(B’)はAに含まれないことがわかります。 よってB’＝φ、つまりf^-1(B)=A、f^-1は全射となります。 また、f(A)＝Bの元はAの元とただ1つ対応し、f^-1(B)＝Aの元はBの元とただ1つ対応していることから、f^-1は単射となります。 以上から、f^-1が写像となるための必要十分条件は、写像fが全単射であるとになります。 この写像f^-1のことを逆写像といいます。

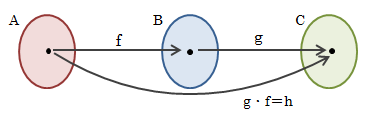
3．4．4．合成写像

3つの集合A、B、Cについて、AからBへの写像をf、BからCへの写像をgとします。 このとき、Aの任意の元aに対し、写像fによってBの元b＝f(a)が決まり、そこから写像gによってCの元c＝g(b)＝g(f(a))が決まります。 このように、Aの元aからCの元g(f(a))への写像hを、fとgの合成写像といい、g・f（g(f(a))であることから順序に注意！！）で表します （本当は小さい○で表しますが、エンコードの都合上・で表記します）。

図3.4.4－1　合成写像

合成写像の前提は、fの終集合とgの始集合が一致することです。 それ以外では合成写像は定義されません。 また、写像f、gが存在すれば、その合成写像g・ｆもまた存在します。

＜合成写像の定理1＞

f：A→B、g：B→Cがともに全射ならば、g・f：A→Cも全射であり、f、gが共に単射ならばg・fも単射になります。 また、f、gが全単射ならばg・fも全単射になります。

＜合成写像の定理2＞

f：A→B、g：B→C、h：C→Dのとき、次の関係が成り立ちます。

(h・g)・f＝h・(g・f)　（結合律）

＜合成写像の定理3＞

恒等写像I_A、I_Bと写像f：A→Bの合成写像について、次の関係が成り立ちます。

f・I_A＝f、I_B・f＝f

また、写像fが全単射であるとき、

f^-1・f＝I_A＝I_B

となります。

3．5．選択公理

選択公理について熱く語られている書籍を紹介しておきます。 非常にわかりやすいのでお勧めなのですが、すでに廃刊となっているようで残念です。

3．5．1．集合族

集合の集合を集合族として扱う書籍が一般的です。 しかし、本サイトでは参考にしている 「集合・位相入門 」（松坂和夫著） に従い、それを集合系と呼んでいます（2.5節）。 では集合族はというと、写像として定義され、その特徴は添数付けられていることです。 添数は数列表現の一般化であることから、まずは数列の一般化から話を始めます。

3．5．1．1．族の概念（数列の一般化）

数列とは、例えば次のようなものです。

数列は、特にiii）をみてわかるように添数である自然数と実数が対応付けられており、写像であることがわかります。 この数列の概念を次のように一般化していきます。

数列：添数である自然数全体Nから実数全体Rへの写像

↓　終集合を一般化

元の列：添数である自然数全体Nからある集合Aへの写像

↓　始集合を一般化

元の族 ：添数である集合Λからある集合Aへの写像

このように、数列の一般化で得られた元の族は写像であり、その始集合Λを添数集合、その元λを添数といいます。 添数集合は明らかに族の定義域になっています。 Λの各元λの、元の族aの像a(λ)を一般にa_λと書きます。このとき、元の族aは次のように表記します。

a＝(a_λ)_λ∈Λ　または (a_λ|λ∈Λ)

（これまではaを集合の元として扱っていましたが、ここでは写像を表していることに注意します）

ここで注目すべき点は、族の表記が“(　)”で囲まれていることです。 これは直積（2.4節）のところでも見たように、順序付られた組の意味をもっており、 集合を表す“{　}”とは明らかに異なります。 例えば数列の例ii）を見ると、数列は(1,(－1),1, (－1),…)として表すのに対し、数列の値の集合は{1,－1}となります （n個の成分（像）表示と2個の元（値）表示の差）。
さて、元の族の値域 {a_λ|λ∈Λ}（以降、{aλ}_λ∈Λで表します）は終集合Aの部分集合となりますが、 族の概念において重視されるのは終集合Aよりも値域であることが一般的です。

3．5．1．2．集合族

族の概念を集合に拡張します。 添数集合Λがあって、族(A_λ)_λ∈ΛによるΛの元λの像A_λが集合のとき、 族(A_λ)_λ∈Λを_集合族といい、その値域 {A_λ}_λ∈Λは集合系を成します。
集合族にも部分集合族が存在します。 ある集合Xがあって、集合族(A_λ)_λ∈Λによるどのλ∈Λの像A_λもXの部分集合であるとき、 (A_λ)_λ∈ΛをXの部分集合族といいます。 このとき集合族(A_λ)_λ∈Λの値域{A_λ}_λ∈Λは、Xのべき集合P(X)の元になります。 例えば、μ、ν∈Λに対していA_μ、A_ν⊂Xのとき、(A_μ,A_ν)はXの部分集合族になります。 また、集合族の値域{ A_μ,A_ν}はXの部分集合系になります（2.5節参照）。
次に、集合族の演算について見ていきます。 添数集合Λがあって、集合族(A_λ)_λ∈Λが与えられているとします。 x∈A_λとなるλ∈Λが少なくとも1つ存在するようなx全体の集合を、集合族の和集合といいます。 それに対し、どのλ∈Λに対しても、x∈A_λとなるx全体の集合を、集合族の積集合といいます。

これらは集合系の和集合、積集合と一致します（2.5節参照）。 なお、集合族の和集合、積集合は分配律が成立します。

(A_λ)_λ∈Λが普遍集合Xの部分集合族の場合、以下に示すドモルガンの法則が成立します。

集合Aから集合Bへの写像をfとし、集合A、Bの部分集合族をそれぞれ(P_λ)_λ∈Λ、 (Q_λ)_λ∈Mとすると、以下の関係が成り立ちます。

3．5．2．集合族の直積

族はそもそも順序づけられた組“(　)”の意味を持つため、直積と関連性を持つのは容易に想像できます。 ここでは、次のようなケースを考えています。 添数集合Λがあって、集合族(A_λ)_λ∈Λが与えられているとします。 Λで定義された写像a（つまり元の族(a_λ)_λ∈Λで、 Λのどの元λに対しても(a_λ)_∈Aλとなる全体の集合を、 集合族(A_λ)_λ∈Λの直積といい、次のように表します。

例えば、Λが自然数全体Nの場合、次のようになります。

なお、直積に対する各Aλを直積因子といいます。 また、集合族(A_λ)_λ∈Λの像が同じ集合Aである場合、すべてのAλの元はAの元でもあります。 この場合、集合族(A_λ)_λ∈Λの直積は、

であり、元の族(a_λ)_λ∈Λの成分1個1個のAへの写像をすべて集めた集合、 つまり配置集合（3.3.4節参照）と捉えることもできます。

3．5．3．選択公理

選択公理（選出公理）の重要性は、写像の概念と強く結びついています。 ただし、選択公理はそもそも公理であるため、証明抜きで受け入れなければなりません。
まずは選択公理を紹介します。

言葉にすると、Λに属するすべての元λに対応する、集合族(A_λ)_λ∈Λの各像A_λが空でないとき、 その直積もまた空でない、ということです。 これをかみ砕くと次のようになります。 添数集合Λに対して集合族(A_λ)_λ∈Λが与えられています。 すべてのλの集合族の像A_λは空集合でないので、各A_λには少なくとも1つ元a_λが含まれます。 従って、このa_λとλを対応付ける写像a（つまり元の族）が必ず1つは存在する、 ということを言っています。 さらに話を進めると、直積の元は順序組（例えば(a_α,a_β,a_γ)）ですから、そのうちの1成分でも欠けると、 例えば(a_α, ,a_γ)は元として成立しません（当然、(a_α,0,a_γ)は成立します）。 しかし、A_λはa_λを必ず含むので、直積は空集合にはなりません。 このとき、直積の元である順序組はすべて同時に並べられるので、各A_λから元a_λを同時に選び出さなければなりません。 この意味から、写像aは各A_λから元a_λを同時性を持って選択しており、選択写像とよびます。 何か当たり前のことのように思えますが、有限の世界ならそれは実証可能です。 しかし、Λが無限集合となると、人間の力では実証は不可能です。 従って、有限の操作から推察して、無限の操作に対しても同時に元を選択することは可能であろうから、 これは疑わずに認めてしまえ、ということが、選択公理の本当のところです。 この選択公理の主張するところは、空でないあらゆる集合に対して選択写像が存在する、ということであり、 選択写像の存在は、その他写像の存在を保証するものである、ということです。 それは写像が、始集合から同時に元を選び出し、1列に並べた上で、 終集合の元と比較しながらそれらの間を対応の規則によって結び付けることに他ならないからです。 つまり一般の写像とは、選択写像と、そこから先の対応の規則を持つ写像との合成写像である、と考えることができます。 従って、選択写像が存在しなければ、一般の写像は存在しえないことになります。

参考文献

関連ページ