1．実生活での集合論

本章では、集合論が数学だけのものではなく、より生活に密着したものであることをイメージできるように話を進めていきます。 そのため、ここでは集合論全般に通じる基礎概念のみに触れ、厳密性は問わず、 極力数学的な表現は使わないようにしています。 厳密な集合論を知らなくても生活の中で集合論の基本的な考え方をうまく使えば、 身の回りの整理整頓、直面する問題の整理と優先順位づけなど様々なことに役立つはずです。 そのことを知ってもらうことがこの章の目的です。 つまり、「どんな人にも集合論は役立つんだ！」 ということを訴えるページにしているつもりです。
さて、実際に集合論で行っていることを要約すると、次のようなものに落ち着きます。

1. 考察範囲を限定する

   集合と元

2. その範囲の中で、“もの”を分類する

   部分集合、類別

3. 各分類ごとの関係を見る

   集合の演算、包含関係

4. 各分類の中にある“もの”に順序をつけ並び替える

   順序数、整列定理

5. 1つの分類を別の分類に対応させる

   対応、写像

実はこれ、整理整頓や問題解決プロセスで行われることと一致していることに気づくと思います。 例えば整理整頓を当てはめてみます。

1. 考察範囲の限定

   本棚の整理　→　集合＝自分の所有本

2. “もの”の分類

   雑誌、マンガ、小説、参考書など

3. 分類間の関係

   雑誌とマンガはよく似てる、小説、参考書はそれぞれ独立

4. 分類の中の順位づけ

   いる／いらない、よく見る／あまり見ない、重い／軽いなど

5. 別の分類に対応

   ゴミとして捨てたり、本棚にしまう位置（雑誌は一番下、マンガはその上など）

このようにうまく集合論を実生活に活用すれば、問題を単純化でき、すっきりと整理整頓ができるようになると思います （とはいえ、現実はいろんなことが複雑に絡み合い、そこにまた感情が入り込むので、そんなに甘くはありませんが．．．）。

1．1．集合の定義

集合とは明確な範囲に属する“もの”で構成された集まりをいい、 それを構成する“もの”を元（要素）といいます。 例えば、次のような例を見ることで、集合かそうでないかを区別することができます。

1. すべての子供たち

   集合

2. その辺にいる子供たち

   集合ではない（その辺ってどの辺？）

3. 公園にいる子供たち

   集合

4. 大きい子供たち

   集合ではない（大きいって何がどのくらい大きい？）

5. 身長150cm以上の子供たち

   集合

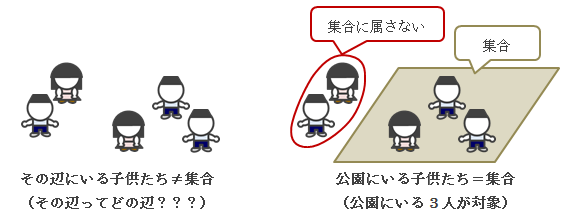
図1.1－1　集合か集合でないか

つまり、集合によって考察対象となる“もの”が明確に限定されることになります。 ただし元と元、つまり集合の中の“もの”と“もの”にある関係性について意識する必要はありません。 今回の例で言えば、公園にいる子供たちが友達同士でも全くの見ず知らずでも何でもかまわない、 ということです。
以上の話から、集合とは“もの”を入れる箱と捉えることができます。 ただし時として、箱の中身が空っぽの場合があります。 集合論ではこの空っぽの箱も1つの集合と考え、 これを空集合（以降φと表します）と呼びます。

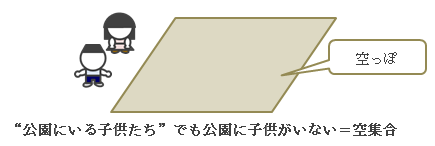
図1.1－2　空集合

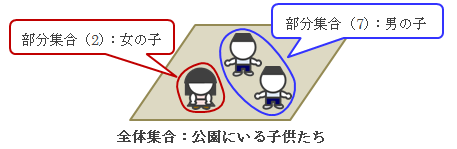
ところで、集合を規定する条件は明確でさえあれば自由に設定することができます （厳密には違いますが、ここではそう見てもかまいません）。 例えば、上述の公園にいる3人の子供たちが、生徒数3人のA小学校の生徒だとすると、 集合“A小学校の生徒たち”と、集合“公園にいる子供たち”を構成する元（子供）は全く同じです。 このように全く同じ元を持つ集合どうしは等しい（同じ）として扱います。 今回の場合、“公園にいる3人の子供たち”＝“A小学校の生徒たち”になります。 結局、すべての元が決まった時点で集合は決定されます。 この考えに基づけば、例えば上述の集合“公園にいる子供たち”は女の子、男の子A、 男の子Bの3人で構成されていますので、 これらを自由に組み合わせることで8個の集合を作ることができます。

1. φ（空集合）
2. {女の子}
3. {男の子A}
4. {男の子B}
5. {女の子、男の子A}
6. {女の子、男の子B}
7. {男の子A、男の子B}
8. {女の子、男の子A、男の子B}　 （＝“公園にいる子供たち”、つまり自分自身）

この（1）～（8）の集合は“公園にいる子供たち”に含まれるか等しいのどちらかになります。 このような集合を部分集合といい、もととなる“公園にいる子供たち”を 全体集合または普遍集合といいます。

図1.1-3　全体集合と部分集合

部分集合が定義されることにより、集合と集合の間には大小の違いが生まれます。 定義により、全体集合は必ず部分集合を含むことから、このような関係を包含関係といいます。 また、空っぽの集合である空集合はすべての集合の部分集合になることは明らかです。

1．2．集合の演算

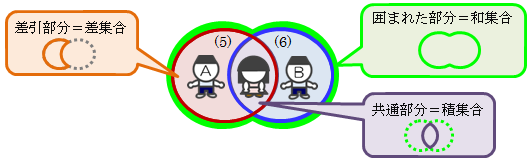
さて、包含関係以外にも上述の集合（1）～（8）の間にはいろいろな関係性があります。 例えば、集合（5）と（6）の間には女の子を共通の元とする関係 （図的には集合と集合が交差した関係）を持っています。 この共通部分を集合（5）と（6）の積集合といいます。 また、集合（5）と（6）の両方に囲まれた集合を和集合といいます。 さらに、集合（5）を（6）で切り取ると女の子が集合（5）から差し引かれます。 このとき残った部分を差集合といいます。 ここに挙げた集合の和、差、積は2つの集合から別の集合を作り出す、 というところに本質的な意味があります。

図1.2－1　積集合、和集合、差集合

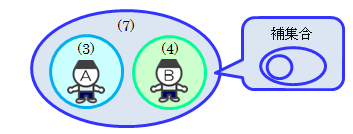
次に、集合（3）と（4）の間には共通する部分がありません。 つまり、集合は交差せず積集合が空集合になっています。 このような関係を集合（3）と（4）は互いに素（独立）な関係といいます。 この互いに素な集合の和集合を特別に直和といいます（今回の例では集合（7）が相当）。 また、集合（3）は集合（7）に完全に含まれています。 このとき集合（7）から（3）を差し引いた差集合のことを補集合といいます （今回の例では集合（4）に相当します）。

図1.2－2　直和と補集合

実は、この集合が互いに素（独立）な状態を以下にうまく作り出せるかが、 実生活において非常に重要です。 その理由は考察対象を絞ることができ、問題を単純化できるからです。 逆に言うと、互いに素でない集合をたくさん作るとそれぞれの集合が絡み合うため、 考察範囲が広くかつ複雑になってしまいます。 いかにうまく問題を整理整頓ができるか？は、考察対象をどれだけ単純化できるか？ につきるといっても過言ではありません。

例えば、整理整頓が下手な人はたいていいろんなものが “ぐちゃぐちゃ”に片づけられています。 “ぐちゃぐちゃ”に片づけると、次どこに片づければよいか、また他の人はどこを探せばよいか混乱し、 さらに“ぐちゃぐちゃ”具合が増幅されてしまいます。 それに対し上手な人は、用途や役割によって物が分類され、それごとに片づけられています。 そうすると、片づける場所を忘れても、用途や役割に合わせて片づければよく、 また、他の人もだいたいこの辺にあるな、という推察のもと物を探すことができます。 ただし、物理学的に見れば“ぐちゃぐちゃな”状態ほど最も自然な状態であり（エントロピーの概念）、 整理整頓をするにはそれなりに自然の力に逆らうためのエネルギーが必要なのは言うまでもありません。 つまり身の回りの整理整頓や問題解決は誰がやっても大変なんです！！

1．3．同値、順序

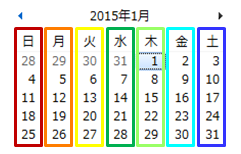
今度は、集合を構成する元の間にある関係について見ていきます。 ある基準（ものさし）で2つの元を見たとき、 それらが同一視できるような関係を同値関係といいます （この言い回しはかなり厳密性に欠けますので要注意！）。 同値関係の最もわかりやすい例として曜日が挙げられます。何月何日という元を曜日で見れば、日曜日、月曜日、・・・、土曜日という形で7日おきに同一視できる日が現れます。また、性別（男、女）を基準にしたり、図形の合同関係や相似関係を基準にしても同値関係が得られます。

図1.3－1　同値関係

この同値関係が集合内に存在すれば、ある元と同値の元を集めて部分集合を作ることができます。 この部分集合を同値類と呼び、同値類を作る作業を類別または分類といいます。 ここでいう分類は、まさにゴミの分類と全く同じで、燃えるゴミ、燃えないゴミ、缶・ビン、・・・ といったものが同値関係の基準になります。 さらに言えば、燃えるゴミの中の使ったティッシュと生ゴミは同値関係になります。 ところで、ある集合を同値類（つまり部分集合）に分類したとき、 同値類どうしは互いに素（独立）な関係になります （もし2つの同値類A、Bが素でない場合、共通の元cがAの元a、Bの元bの両方と同値関係にあります。 そうなると当然aとbも同値関係になることから、AとBは一つの同値類としてまとめられることになります）。 従って、ある集合を同値類に分割することを直和分割といいます。
実生活で直面する問題に対して、この直和分割こそが、先ほどの問題整理のための必殺の方法です。 その理由は前述のとおりであり、いかに同値と見なせる“ものさし”をうまく設定するか？ が腕の見せ所になります。
次に、2つの元を比較してその違いに対し順序付けを行います。 順序といっても“大小”、“高低”、“前後”、“優劣”など様々ですが、 どれも“大小”をもとに考えられるものです （例えば“高低”＝高さの大小、“前後”＝位置の大小、“優劣”＝優位の大小）。 そこで2つの異なる元a、bに対して、「aはb以上（aはbより小さくない）」または 「bはa以上（bはaより小さくない）」のどちらか一方に確定できるとき、 a、bは比較可能であるといい、このときのa、bの関係を順序関係といいます （これもまた同値関係同様厳密ではないので要注意！）。 また、順序関係を持つ集合を順序集合といい、 すべてが比較可能である集合を全順序集合、 そうでないものを半順序集合といいます。
順序付けは、実生活では優先順位を付け、どれが一番大事とか、 何から一番最初に手を付けないといけないか？を判断する材料になります。 また、必ずしも順序付け可能でなくてもよいところが現実とうまくマッチしていると思います。

1．4．写像

最後に、集合の元が別の集合の元と何らかの関係性を持つことがあります。 例えば“食材”という集合は魚、肉、野菜を、それに対し“晩ごはん”という集合は、 お刺身、焼肉、サラダを元としている場合を考えます。 このとき集合“食材”の魚は料理することで“晩ごはん”の1つの元であるお刺身と対応関係で結びついています。 また肉は焼肉と、野菜はサラダと対応関係で結びついています。 このときの料理のことを写像といい、“食材”を始集合、“おかず”を終集合といいます。 もう少し抽象的に言うと、ある集合（始集合）の元がある規則（手段）によって別の集合（終集合）の唯一の元と関係を持つとき、 その規則を写像といいます。

図1.4－1　写像

実は写像について1つ意識すべき点があります。 それは写像ありきで終集合が決定されるのではなく、始集合と終集合があって写像が決定される、ということです。 この考え方は実生活において非常に役立ちます。
実生活における写像の重要性は、まさに“技術”と等価であることだと思います。 どういうことかというと、本章始めの本棚の整理で言えば、どういった形で整理するか？を決める技術が写像にあたります。 このとき、終集合をどうするかイメージしておくことが大事です。 最後の姿をイメージしなければ、どう整理整頓すればよいかわからなくなってしまいます。 そのため、終集合を使い勝手でつくるのか、本の種類でつくるのか、はたまた本棚が安定するよう重さの違いでつくるのかは、 実際に整理整頓する人によって決める必要があります。

1．5．本章のさいごに

この章では、実生活に密着した形での集合論の概要を見てきました。 その意図は本章の初めにも書いたように、数学が好きとか嫌いとか関係なく 「どんな人にも集合論の考え方は役に立つんだ」ということを訴えたかったためです。 集合論の論理構成、考え方を活用すれば、複雑に絡み合った問題もうまく整理がつくようになると思います。 今回は集合論を実生活に当てはめてみましたが、他の自然科学 （数学だけでなく、物理でも科学でも生物学でも天文学でも）の考え方も実生活に役立つことは多々あると思います。 自然科学は決して難しいものでも高尚なものでもありません。 おいしいところを必要に応じて活用していければ、手軽に自然科学を楽しむことができると思います。

参考文献

関連ページ