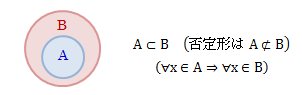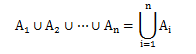2．集合の基本概念

2．1．集合の概念

2．1．1．集合と元

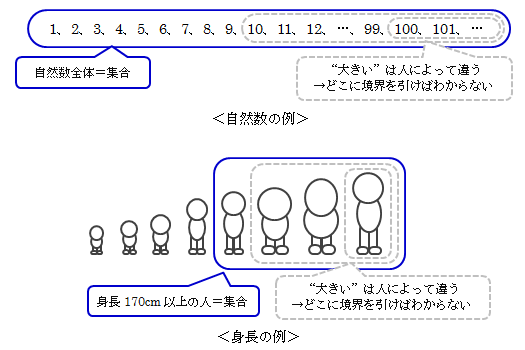
集合とは“もの”の集まりですが、数学的には以下の3つが求められます。

1. 考察範囲の確立
2. 明確な条件（性質）の適合
3. 個々の“もの”の判然たる区別

• 集合であるもの

  すべての自然数の集まり、身長170cm以上の人

• 集合でないもの

  大きな自然数の集まり、背の高い人

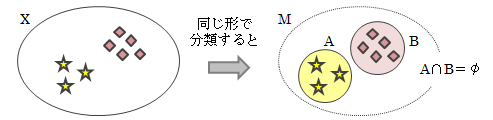
図2.1.1－1　集合と集合でないものの例

「大きな」とか「背の高い」は範囲が不明確です。また「変な」というのはどういう変かわかりません。 集合は、明瞭な境界が引けるという意味で、箱のようなものと捉えることができます
人は何かを考察する際、何らかの範囲を設定します。 そうしなければ考察対象は無数に存在することになり、有限な人間では処理できなくなってしまいます。 その考察範囲を確立（上記（1））する際、もし明確な条件（上記（2））が提示されなければ、 上図2.1－1の例のように、集合を設定するための境界を引くことができません。 逆に明確な条件が提示されれば、集合に属する“もの”、つまり考察対象を特定できます。 あるいは、集合に属する“もの”がすべて既知であれば、まさにその“もの”自体の所属が条件となって集合を構成します。 つまり集合は、それを構成するすべての“もの”が決まれば特定されます。
さて、集合を構成する“もの”を元といいます。 元は（3）の条件を満たす限り、数、記号、文字、関数、集合など何でも構いません。 ただし、集合論の考察対象は集合であることから、集合を元とする集合を“集合”というと、 どの話をしているか分からなくなります。 従って、集合を元とする集合を集合系と呼ぶことにします（2.5節参照）。
集合を元の個数によって区別する方法があります。

• 空集合

  元を持たない集合（0個）

• 有限集合

  元が有限個ある集合　例）1～100の整数

• 無限集合

  元が無限個ある集合　例）1～100の実数

空集合の概念は重要です。空集合の存在は公理として認めるもので、証明することは出来ません。 空っぽなのに集合？と思われるかもしれませんが、数学上必要あってのことです^＊。 とりあえずは空き箱が準備されてると考えておけばよいかと思います。
＊空集合によって（順序）数を作ることが可能なため、非常に重要な概念です。 これに関するわかりやすい説明は以下の書籍にあるので参考にしてみてください。

2．1．2．集合の表記法

ここで、数学における集合の表記法について見ていきます。 集合をA、その元をaで表すとき「aはAの元である」、その否定形「aはAの元でない」は下記のように表します。

次に、集合Aが元a、b、c・・・で構成されるとき、そのすべての元を書き込めるか、その元の特徴が明確であるならば、

A＝{a,b,c…}

といった形で表します。この表記方法を外延的記法といいます（自然数全体などはこれに当てはまります）。 しかしながら、外延的記法だけでは表せない集合もあります（例えば実数全体など）。 そのため別の表記法として、集合Aの任意の元xが条件Cを満足することをC(x)で表したとき、

A＝{x|C(x)}

この表記方法を内包的記法といいます。xはAのあらゆる元を代表的に表す記号であり、変数といいます。 言い換えると、変数とは考察対象を一つの記号で表し、その中身はある条件下で自由に変化できる“もの”を意味します。 なお、空集合φは次のように表します。

φ＝{ }＝{x|C(x)}

（C(x)を満たすxはなくても内包的記法はそのまま使えます）

2．2．集合間の関係

2．2．1．相当関係

前節で見たように、集合はそれを構成するすべての元が決まれば特定されます。 従って、2つの集合A、Bが全く同じ元で構成されるとき、集合AとBは等しいと認めます。 これは外延性公理と呼ばれるもので、証明抜きで受け入れる必要があります。この外延性公理を集合論的に言いまわせば、 「A=Bとは、Aの任意の元は同時にBの元でもあり、Bの任意の元は同時にAの元でもある関係」、ということになります。

A=B ⇔∀x　(x∈A ⇔ x∈B)

2．2．2．包含関係（部分集合）

集合A、Bにおいて、Aのすべての元xがBの元となるとき、AはBの部分集合といいます。 このとき、集合Bは集合Aを包含しているので、このような関係を包含関係といい、 記号で表すと次のようになります。

図2.2.2－1　部分集合の定義

部分集合の定義から、そこにはA＝B（相当関係）も含まれ、相当関係と包含関係の間に次の関係が成り立ちます。

A⊂B　∧　B⊂A　⇔　A = B

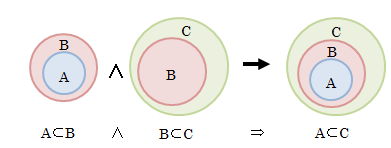
それに対し、A≠BのときのAをBの真部分集合と呼びます。 なお、空集合φは、その定義からあらゆる集合の部分集合になることは明らかです。 また、部分集合の特徴として、推移律が成り立ちます。

図2.2.2－2　部分集合の推移律

この包含関係が定義されることで、集合の大小関係が意識されます。 最後に例として、A = {a,b,c}の部分集合をすべて（8個）挙げてみます。

φ、{a}、{b}、{c}、{a,b}、{a,c}、{b,c}、{a,b,c}（= A）

2．3．集合の演算

本節の話は、2つあるいは複数の集合から別の集合を作る、という意味で和、差、積といった演算の概念を集合に入れ込んでいます。 これらによって集合の範囲をいろいろと定義しなおすことができ、ある意味で考察対象の範囲を調整できることになります。

2．3．1．和集合

2つの集合A、Bについて、Aの元とBの元をすべて含む集合をAとBとの和集合といい、次のように表します。

図2.3.1－1　和集合

集合AとBに共通の元が存在する場合（上左図）を集合は交わるといい、 そうでない場合（上右図）を互いに素（独立）であるといいます。 また互いに素な集合の和を直和といいます。
和集合には次のような演算則定理が成り立ちます。

1. A⊂A∪B、B⊂A∪B
2. A⊂C、B⊂C　⇒　A∪B⊂C
3. A∪A＝A（巾等律）
4. A∪B＝B∪A（交換律）
5. (A∪B)∪C＝A∪(B∪C)＝A∪B∪C（結合律）
6. A⊂B　⇒　A∪B＝B
7. A⊂B　⇒　A∪C⊂B∪C
8. φ∪A＝A

（5）は、括弧をどこにおいても結論は変わらないことを意味しています。 一般に、n個の集合A_１、A₂、・・・、A_nがあるとき、 それらの和集合は次のように表します。

2．3．2．積集合

2つの集合A、Bについて、AとBの両方に属する元を持つ集合、 つまりAとBの交わった部分の集合を積集合といい、次のように表します。

図2.3.2－1　積集合

前述（2.3.1節）した集合AとBが互いに素な関係とは、A∩B＝φ（空集合）の場合を指します。
積集合には次のような演算則定理が成り立ちます。

1. A∩B⊂A、A∩B⊂B
2. C⊂A、C⊂B　⇒　C⊂A∩B
3. A∩A＝A（巾等律）
4. A∩B＝B∩A（交換律）
5. (A∩B)∩C＝A∩(B∩C)＝A∩B∩C（結合律）
6. A⊂B　⇒　A∩B＝A
7. A⊂B　⇒　A∩C⊂B∩C
8. φ∩A＝φ

また、和集合と積集合の間には以下の演算則定理が成り立ちます。

1. (A∪B) ∩C＝(A∩C) ∪ (B∩C)
2. (A∩B) ∪C＝(A∪C) ∩ (B∪C)
3. (A∪B) ∩A＝A（吸収律）
4. (A∩B) ∪A＝A（吸収律）

2．3．3．差集合

2つの集合A、Bについて、Aの元であってBの元でないものすべてで構成される集合を、 A、Bの差集合といい、A－BまたはA＼B（“／”ではないですよ）で表します。 これを内包的記法で表すと、次のようになります。

図2.3.3－1　差集合

2．3．4．全体集合

考察対象全体を表す集合のことを全体集合または普遍集合といいます。 ここでは、一般的に全体集合として扱われる数の集合について紹介だけしておきます。

• 自然数全体

  N = { 0,1,2,3,…,n,… }

• 整数全体

  Z = { …,-3,-2,-1,0,1,2,3,… }

• 有理数全体

  Q＝{ a/b|a,b∈Z,a≠0 }

• 無理数全体

  R－Q

• 実数全体

  R

• 複素数全体

  C = { z|z = x + yi, (x∈R, y∈R) }　（i：虚数）

全体集合Xに対する部分集合Aの差集合を補集合と呼び、一般にA^C（＝X－A）で表します。 このとき、A^Cを内包的記法で表すと、次のようになります。

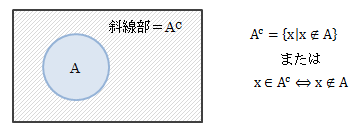
図2.3.4－1　補集合

補集合A^Cの定義から、次の演算則定理が成り立ちます。

1. A∪A^C＝X、A∩A^C＝φ
2. A^CC＝A
3. φ^C＝X、X^C＝φ
4. A⊂B　⇔　A^C⊂B^C
5. (A∪B)^C＝A^C∩B^C（ドモルガンの法則）
6. (A∩B)^C＝A^C∪B^C（ドモルガンの法則）

（5）（6）については、ドモルガンの法則と呼ばれています。

2．4．直積

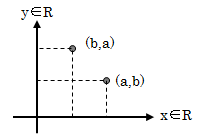
前述の集合の演算とは別の方法で、新たな集合を作るのが直積になります。 集合Aの元aと集合Bの元bから作られる、順序づけた組（対）(a,b)のすべてを元とする集合を直積といい、 以下のように表します。

A×B＝{(a,b)|a∈A,b∈B}

このとき重要なのは“aとbの順序”です。 aを第1成分、bを第2成分といい、必ずAの元が第1成分、Bの元が第2成分として表記されます。 このとき、a≠bでない限り(a,b)≠(b,a)となります。 “(　)”を使った表記の例として、ベクトルや数列が挙げられます。 直積の定義から、A×Bの交換法則は成り立ちません。

A×B≠B×A

また、直積は次のような形で一般化できます。

A₁×A₂×…×A_n＝｛（a₁, a₂,…,a_n）| a_i∈A_i（i＝1,2,…,n）｝

最もわかりやすい直積の例は、集合A、Bがともに実数全体Rの場合です。 そもそも実数全体Rは一本の数直線で表せます。 従って直積R×R＝R2は2本の数直線で表せ、下図のように視覚的に表せます。 この図を見れば、直積に交換法則が成り立たないことは一目瞭然です。

図2.4－1　直積R2の例

2．5．集合系

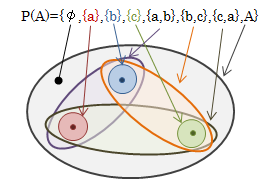
集合を元とする集合のことを集合系^＊1といいます。 集合とあえて区別しているのは、集合論の考察対象が集合であること、 集合の集合からは集合論の矛盾（ラッセルの矛盾）が導かれること、などが挙げられると思います。 （なお、集合系のことを集合族と呼ぶこともありますが、 本サイトでは参考としている下記文献に習って、使い分けることにします。）

集合は必ず部分集合を持ちます（空集合があるため）。 従って、ある集合に付随する集合系を作ることができます。 その1つとして、集合Aのすべての部分集合を元とする集合系をべき集合といい、P(A)で表します。
またべき集合P(A)のいくつかの元から集合系を作ることもできます。 このような集合系を集合Aの部分集合系といいます。 例えばA、BをXの部分集合とすると、Xの部分集合系MはA、B∈MでありM⊂P(X)になります。 以下にべき集合と部分集合系の例を挙げてみます。 2つの元a,bで構成される集合Aの部分集合は4個であり、Aのべき集合P(A)は次のようになります。

図2.5－1　べき集合イメージ

また、べき集合P(A)のいくつかの元から集合系を作ることもできます。 このような集合系を集合Aの部分集合系といいます。 例えば上図{a}と{b,c}はAの部分集合であり、これらを元とする集合系を考えれば、 それはAの部分集合系でありM＝{{a},{b,c}}⊂P(X)になります。 ところで、1つ注意しなくてはならないのが、

P(φ)＝{φ}≠φ

であることです。これは、φの元が0個なのに対し{φ}の元は1個あるためで、 {φ}が空集合でないことは明らかです。
集合系があれば、そこから集合を作ることもできます（当たり前といえばそれまでですが）。 集合系Mに属する集合のすべての元で作る集合を、集合系Mの和集合といいます。

図2.5－2　集合系の和集合

集合系Mに属するすべての集合に共通な元全体の集合を集合系Mの積集合といいます。

図2.5－3　集合系の積集合

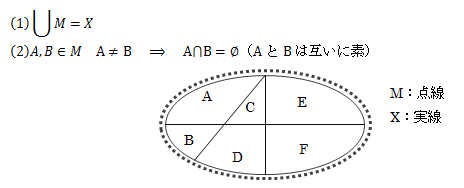
集合Xとその部分集合系Mについて次の2つが成り立つとき、集合系MはXの直和分割といいます。

図2.5－4　直和分割

直和分割を具体的に言えば、集合Xの部分集合が互いに素となるXの部分集合系をつくることになります。 直和分割は、次節で示す同値関係と非常に密接な関係があります。

2．6．元間の関係

これまでは集合に視点を置いてきましたので、今度は元に視点を置いて見ていきます。 もともとは集合を定義する上で元と元の間の関係を考慮する必要はありませんでした。 ですが“もの”が集まればそれらは似ているのか？何か大小、前後、優劣などの違いはあるのか？ といったことが興味の対象になってきます。 そこで、集合の中に“関係”といった識別の基準となる概念を持たせることが、本章の目的になります。

2．6．1．同値関係

元同士が同類と見なせるかどうかは非常に重要です。同類と見なせるもので部分集合を作れば、その考察を簡素化出来ます。 そこで、元同士を同類と見なせるものさしとなる“関係”を集合に定義します。 集合Xの元間に定義した関係“～”が以下の3条件を満足するとき、その関係を同値関係といいます。
x、y、z∈Xに対し

• 反射律

  x～x

• 対称律

  x～y　⇒　y～x

• 推移律

  x～y、y～z　⇒　x～z

上記3つの条件をあわせて同値律といいます。 この同値関係の定義自体は非常に抽象的でわかりにくいですが、それを満たす最もわかりやすい例が等号“＝”です。

（1）x＝x、（2）x＝yならばy＝x、（3）x＝y、y＝zならばx＝ｚ

同値関係は等号関係の一般化といえ、“≡”で表されるような合同式（mod）や図形の合同、相似関係から、 趣味や専攻の一致なども同値関係にあてはまります （記号“～”は関係を表す変数と考えることができます）。
集合Xに同値関係があればそれを基準に部分集合をつくることができます。 ∃a∈Xに対してaと同値な元で構成される部分集合C(a)を、同値関係～によるaの同値類といいます。 同値類C(a)には以下が成り立ちます。
C(a)＝{x|x∈X、a～x}に対し

1. a∈C(a)（つまりC(a)≠φ）
2. a～b　⇔　C(a)＝C(b)
3. C(a)≠C(b)　⇒　C(a)∩C(b)＝φ

＜証明を見る＞
集合Xを同値類に分割することは、その定義から互いに素な部分集合をつくること、 つまりXの直和分割（互いに素な集合を元とする集合系をつくること）に他なりません。 これは同値関係～に基づく集合Xの部分集合系Mを作ることであり、類別または分類といいます。 また、この部分集合系M、つまり同値類全体の集合を集合Xの関係～による商集合といい、 X／～で表します（つまり商集合は集合系です）。

図2.6.1－1　類別（分類）と同値類の関係

ここで重要な定理を紹介します。 定理：集合Xが類別される必要十分条件は、Xに同値関係が存在することである

2．6．2．順序関係

順序といえば、大小、前後、高低、優劣など相反関係をはっきりさせるものです。 そこで、集合に元同士の比較において順序を判別できるものさしとなる“関係”を定義します。 集合Xの元間に定義した関係“≦”が以下の3条件を満足するとき、 その関係を順序関係といい、順序関係≦を持つ集合を順序集合といい(X,≦)で表します。
x、y、z∈Xに対し

1. 反射律

   x≦x

2. 対称律

   x≦y、y≦z　⇒　x≦z

3. 推移律

   x≦y、y≦x　⇒　y＝x　（ここが同値関係との違い！）

順序については、等号を含む≦（以上）／≧（以下）のほかに、 等号を含まない＜（より大きい）／＞（より小さい）があります。 関係＜については

が成り立ちます。
順序集合(X,≦)の元x、yがx≦yまたはy≦xのどちらかに定まることを比較可能といい、 すべての元が必ず比較可能であるものを全順序集合、そうでないものを半順序集合といいます。 全順序集合については、その空でない部分集合も必ず全順序（部分）集合になることは明らかです。
この順序関係を定義することによって、次の概念が定義されます。 その前提として、順序集合（X,≦）が与えられているとします。

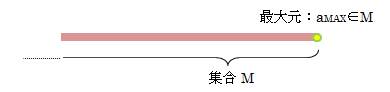
（1）最大元／最小元

（2）極大元／極小元

（3）上限／下限

（4）双対概念

参考文献

関連ページ