集合論
3.写像
3.1.写像のイメージ
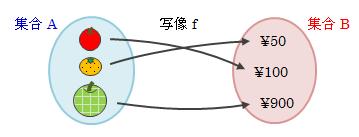
ここでは写像のイメージをつかむことに専念します。 八百屋さんでリンゴ、ミカン、メロンを1個ずつ売っています。 リンゴは\100、ミカンは\50、メロンは\900とします。 このとき次のような集合を2つ考えます。- 果物の集合
- A={リンゴ、ミカン、メロン}}
- 値段の集合
- B={\50、\100、\900}
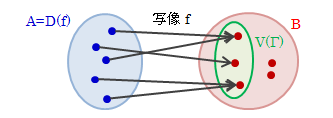
図3.1-1 写像のイメージ
写像は、Aの任意の元に対してBのただ1つの元と対応していなければなりません。 例えば、リンゴが\100と\900の両方と対応してはいけませんし、値段のどの元とも対応しないのもNGです。 この内容を、次節で数学的に定義します。
3.2.対応と写像
前節で見たように、“写像”は集合間にある何らかの“対応”を定めるものです。 つまり、“対応”という概念にもとづいて“写像”は定義されています。3.2.1.対応の定義
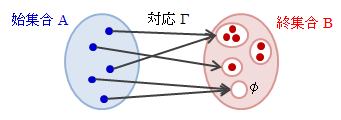
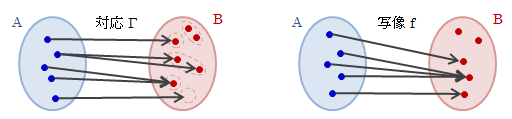
対応とは、2つの集合A、Bがあって、Aの任意の元aと、Bのある1つの部分集合を対応付ける規則Γのことをいい、 Γ:A→Bで表します。 また、この部分集合をΓによるaの像といいΓ(a)で表します。 さらに、Aを始集合、Bを終集合といいます。 対応は非常にゆるい概念で、aの像Γ(a)は空集合でも、 a≠a’の像がΓ(a)=Γ(a’)であっても構いません。図3.2.1-1 対応の概念
3.2.2.写像の定義
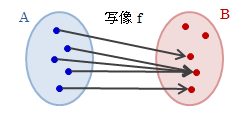
対応をもとに、写像を定義します(つまり、写像は対応の一種です)。 写像とは、2つの集合A、Bがあって、Aの任意の元aと、ただ1つの元bを持つBの部分集合{b}を対応付ける規則fのことをいい、 f:A→Bで表します。 対応と同様、像はf(a)で表し、写像の場合f(a)={b}となります。 ただし、f(a)はただ一つの元bしか持たないため、bは確定的です。 従って、写像においてはf(a)=bとしても実質問題ないため、そのように扱います。 結局のところ写像とは、Aの任意の元と、それぞれに対してある1つのBの元を対応付ける規則に他なりません。図3.2.2-1 写像
またf(a)=bとなるBの元を値といいます。値と像は次の点で区別されます。 a1、a2∈Aでa1≠a2のとき、 写像f:A→Bによる像f(a1)、f(a2)がともにbならば、 結果的にはf(a1)=f(a2)=bですが、 意味合い的にはf(a1)はa1の像であってa2の像ではなく、 f(a2)はa2の像であってa1の像ではありません。 bは像の結果を表している、という点で値と像は区別されます。
3.2.3.定義域と値域
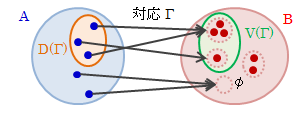
2つの集合A、Bがあって、対応Γ:A→Bが定義されるとき、a∈Aの像Γ(a)が空でないAの元すべて集めた集合を、 Γの定義域D(Γ)といいます。 それに対し、Γ(a)が空でないBのすべての部分集合の和を値域V(Γ)といいます。 定義域はAの部分集合であり、値域はBの部分集合であることは明らかです。- 定義域
- D(Γ)={a|∀Γ(a)≠φ,a∈A }
- 値域
- V(Γ)={b|b∈∪Γ(a) ,a∈A }
図3.2.3-1 対応の定義域・値域
次に、定義域と値域を写像f:A→Bに適用します。このとき、写像の定義により始集合Aと定義域D(f)は一致します。 それに対し、a∈Aの像f(a)をすべて集めた集合を値域V(f)といいます。
- 定義域
- D(f)=A<
- 値域
- V(Γ)={f(a)| a∈A }
図3.2.3-2 写像の定義域・値域
3.2.4.対応と写像の比較
まずは、対応と写像の定義を見てきましたので、ここではそれらの比較を行います。 写像を定義する際、まずは対応の定義を当てはめ、その上で像である部分集合の元の一意性によって、 写像は元と元との対応という形になりました。 今度は逆に、元と元との対応、という観点から“対応”Γ:A→Bの持つ意味について見てみます。 そもそも終集合Bの部分集合は、Bの元を任意に組み合わせて作ることができ、さらには空集合も認めています。 従って、始集合Aの元がBの複数の元と対応していようが、 ただ1つの元と対応していようが、Bに相手がいなかろうが構わない、ということを言っています。 つまり対応は、2つの集合が与えられる限り、それらには何らかの間柄があることを明示する (対応がないことも含め)、という意味があります。 それに対し、写像は始集合との対応が必ず存在するため、ある種対応に厳しい条件が付加されたもの、 つまり対応の一種である、と捉えることができます。図3.2.4-1 対応と写像の違い
今度は、対応、写像ともに重要視しなければならない点について見ていきます。 まずは、2つの集合が与えられた上で対応、写像の定義がなされている、ということです。 つまり、始集合と対応または写像があって終集合が作られるわけではない、ということです。 ただし、写像において終集合を重視しない立場で議論されることはあります。
次に、対応、写像にも相当関係が存在します。 2つの対応Γ、Γ’がともに集合AからBへの対応であるとき、Aの任意の元aに対してΓ(a)=Γ’(a)が成り立つとき、 ΓとΓ’は等しい、とします。 このとき、始集合Aと終集合Bも一致していることが前提条件となります。 これは写像にもそのまま当てはまります。 ただし写像において、終集合を重視しないでよい場合があります。 この場合、写像の相当関係に対して終集合は必ずしも一致する必要はありません。 その条件としては、写像fの値域V(f)をどちらの終集合も含んでいればよい、というものです。
3.2.5.簡単な写像
ここでは、写像の中で最も簡単なものを2つ挙げておきます。(1)定値写像
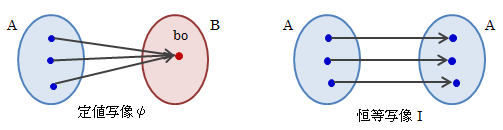
A→Bの写像ψについて、Aの任意の元aが、集合Bのある1つの元b(2)恒等写像
集合Aの任意の元aをa自身に写すとき、つまりa=I(a)のとき、Iを恒等写像といいます。図3.2.5-1 定値写像と恒等写像
3.2.6.写像の縮小・拡大
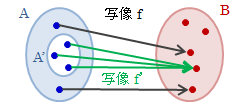
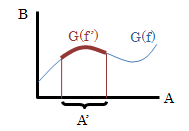
集合Aの部分集合をA’とします。 今、写像f:A→Bと写像f’:A’→Bがあって、A’のすべての元aに対してf(a)=f’(a)が成り立つとき、 f’をfのA’への縮小(制限)といい、逆にfをf’のAへの拡大といいます。 これを図にすると以下のようになり、写像の縮小・拡大はその定義域の縮小・拡大を意味しています。図3.2.6-1 写像の縮小
写像の縮小は、A’つまり縮小する目標先が決まっていることから一意に決まりますが、 拡大は出所A’が決まっているだけで、それよりも大きい集合であればよいので多数存在するのが一般的です。
3.3.グラフ
中学生ぐらいで初めて習ったグラフは、関数の特徴を視覚的に表す図でした。 これを集合論では数学的表記で明確に定義します。 ここでは2.4節で定義した直積の概念が必要になります。3.3.1.関数
関数とは、写像の始集合、終集合をそれぞれ数によって構成される集合で与えられたものです。 始集合の元xの関数fによる像f(x)が終集合の元yと一致するとき、一般にy = f (x)で表します。通常関数は、 ある法則性を持った数式によって表せるもの、との認識を持ちますが、 集合論での関数はもっと広義で、法則性のない単なる数と数の写像も含みます。3.3.2.グラフ
グラフとは、端的に言えば順序対を元とする集合です(だから直積の概念が必要になります)。 グラフは対応や写像に対して、次のように定義されます。- 対応のグラフ
- D(f)=A
- 写像のグラフ
- G(f) = {(a,f(a))|a∈A}
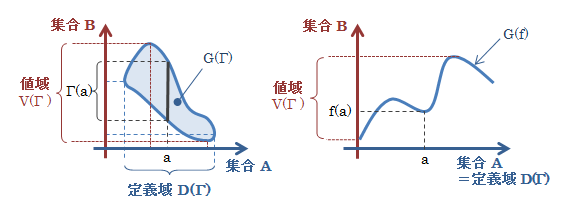
図3.3.2-1 対応と写像のグラフ
二つのグラフを見れば、対応と写像の違いが視覚的に明らかになります。 なお、図中記したG(Γ)を対応のグラフ、G(f)を写像のグラフといいます。 またグラフの定義から、a∈A、b∈Bに対し(a,b)∈G(Γ)であることと、b∈Γ(a)であることは同等であることがわかります。 よって、グラフを用いた形で対応とその定義域、値域を定義することもできます。
- 対応
- Γ(a) = {b|(a,b)∈G(Γ) }
- 定義域
- D(Γ) = {a|∃b((a,b)∈G) }
- 値域
- V(Γ) = {b|∃a((a,b)∈G) }