スペクトル解析
信号とデータサンプリング
2．1．信号データのデジタル化
物理現象を表す信号は連続的な数値として出力され、これをアナログ信号と呼びます。 この信号をコンピュータで処理する場合、不連続な数値に変換しなければなりません。 これは、コンピュータの計算できる桁数が有限であることに起因しています。 この不連続な数値をデジタル信号と呼び、アナログ信号からデジタル信号に変換することをAD変換と呼びます。 アナログ信号をデジタル化するためには、離散化と量子化の作業が必要になります。 離散化は時間を不連続化（とびとびの値）することをいい、量子化は出力値を不連続化することをいいます。 信号をデジタル化した例を下図2.1－1に示します。 下図における格子の横線は時間の離散化に、縦線は出力の量子化に該当します。 そのため、格子点座標がデジタル信号として取り得る値になります。 アナログ信号は必ずしも格子点上を通るとは限りませんので、デジタル信号はアナログ信号を近似的に扱う、という意味も含まれます。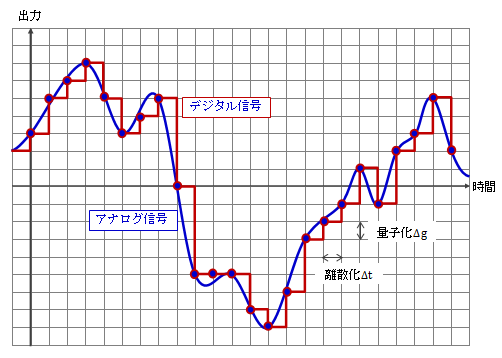
図2.1－1 信号のデジタル化
（この図は適当ですので、正確なものは別サイトをご参照ください）
ここで、上図の横線1目盛分である時間の離散化間隔をΔt、縦線1目盛分である出力の量子化間隔をΔgとします。
このとき、デジタル信号はある自然数n、kを用いて（nΔt、kΔg）で表せ、
「時刻nΔt から(n+1)Δt間の出力値をkΔgで代表する」という意味を持ちます。
これは、アナログ信号に対応するデジタル信号としてある区間内の代表値を選択する、という意味からサンプリング（標本化）と呼びます。
Δtはサンプリング間隔であり、一定間隔で繰り返されることから周期の意味を持つため、サンプリング周期と呼びます。
また、この逆数（1/Δt）をサンプリング周波数と呼びます。
2．2．サンプリング定理
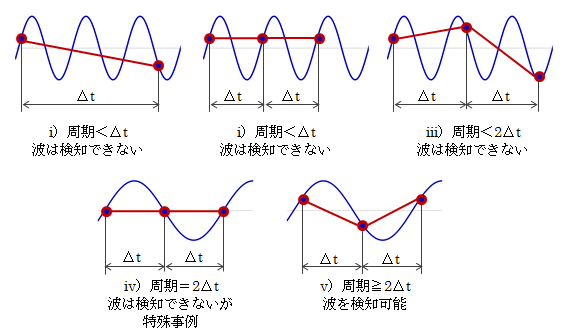
周波数分析を行うためのデータを取得する際、サンプリングに関する制約があります。デジタル化された時系列データを三角関数の級数和として表すことがフーリエ変換（実際は級数展開）ですから、 デジタルデータから波の形を抽出できなければなりません。 図2.2－1で見ればわかるように、もしデータの中にサンプリング周期Δtの2倍より小さい波があった場合、その波は検知できません。 従って、Δtは検知したい最も小さい周期成分の波の半分以下としなければなりません。 これを周波数で言い換えると、サンプリング周波数は検知したい波の最大周波数の2倍以上としなければなりません。 例えば100Hzまで分析したい場合は、サンプリング周波数を200Hz以上としなければなりません。 この最低周波数（100Hzに該当する周波数）をナイキスト周波数と呼び、このようなサンプリング制約をサンプリング定理と呼びます。
図2.2－1 サンプリング周期による波の検知条件
上図iv）はサンプリング定理を満たしているものの、波を検知できない特殊事例になります。 その場合は、観測開始時刻を少しずらせば波として認識出来るようになります。＜サンプリング周期を決める具体的な例＞
例えば、100Hzまでの周波数特性（ナイキスト周波数100Hz）が知りたい場合、 サンプリング定理により最低200Hzのサンプリング周波数が必要となります。 この逆数がサンプリング周期Δtとなりますので、Δt＝0.005秒以下とする必要があります （ただし、後に出てくるエイリアジングの影響は無視します）。
