スペクトル解析
1．3．パワースペクトル
1．3．1．データのエネルギーとパワー
時系列データにもいろいろあって、変動が大きいものもあれば、あんまり変動しないものもあります。 変動が大きいとは振幅が大きいことを意味し、変動が小さいとは振幅が小さいことを意味しています。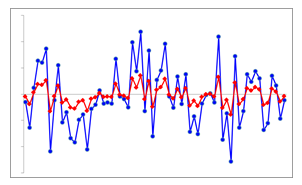
図1.3.1－1 時系列データの変動例
ところで、波の運動エネルギーは振幅の二乗に比例しますので、 時系列データx(t)を構成する波に対してもその考え方を適用すると、データのエネルギーを以下のように定義できます。\[
E
=
\int_{-\infty}^{\infty} \{ x(t) \}^2 dt
\tag{1.3.1-1}
\]
時間は無限と考えられますが（人間から見れば）、実際に取得するデータは有限長になります。
従って、その計測時間がTのとき、積分範囲を便宜上－T/2～T/2として上式を書き直すことで、測定した時系列データの持つエネルギーが定まります。\[
E
=
\int_{-T/2}^{T/2} \{ x(t) \}^2 dt
\tag{1.3.1-2}
\]
振幅の二乗を取る意味を別の角度から見ることもできます。
もし振幅をそのまま積分してしまうと、振幅は正負を持つ場合があることから、変動が大きくてもその積分が“0”になってしまうことがあります。
これでは変動の大小を区別することは出来ません。
ただ、絶対値では数学的な処理が難しくなるため、二乗をとるのが最も妥当と言えるでしょう
（これは分散と同じ考え方になります）。
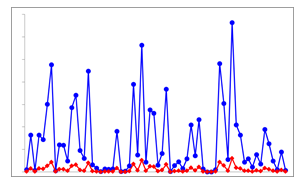
図1.3.1－2 時系列データのエネルギー例
（図1.3.1－1の振幅を二乗したもの）
さて、時系列データの時間の扱いが－∞＜t＜∞とする場合、エネルギーも∞となる場合があります。
∞は処理に困りますので、この場合は単位時間当たりのエネルギー、つまりパワーを用いる方が適切です。
時系列データの計測時間または周期をTとする場合、計測時間または1周期平均のパワーは次式で表せます。\[
P_T
=
\frac{1}{T}\int_{-T/2}^{T/2} \{ x(t) \}^2 dt
\tag{1.3.1-3}
\]
Tを∞にする場合はその極限を取ればよく、\[
P_T
=
\lim_{n \to \infty}
\frac{1}{T}\int_{-T/2}^{T/2} \{ x(t) \}^2 dt
\tag{1.3.1-4}
\]
となります。
また、瞬時のパワーが欲しい場合はT→0の極限をとればよいことになります。
1．3．2．パワースペクトル
前節では、時系列データのエネルギーとパワーを定義しました。 これは、時系列データに含まれるすべての成分波が持つエネルギー、パワーそれぞれの合計を計算したものです。 そのため、時系列データをスペクトル分解することで、各周波数成分波が持つそれぞれのパワーがどの程度あるか？を知ることができます。 このとき、時系列データの持つエネルギーは、スペクトル解析を行っても不変です。 これは、（1.3.1－1）式に（1.2－1）式を代入するとわかりますが、時間t、周波数fともに積分されているので、 エネルギーEはt、fを変数として含まないためです。
そこで、各周波数成分ごとのパワーをP(f)で定義すると、前節で定義した時系列データのパワーPTは次式で表せます。\[
P_T
=
\int_{-\infty}^{\infty} P(f) df
\tag{1.3.2-2}
\]
この各周波数成分が持つパワーP(f)のことをパワースペクトル（Power Spectrum）またはパワースペクトル密度関数（Power Spectrum Density Function）と呼びます。
1．3．3．実際のデータ処理
実際の時系列データx(t)は無限ではなく有限です。 従って、そこから得られるエネルギーEもまた有限であり、計測時間をTとすると、次のようになります （今回は極限をとりませんので0～Tで積分します）。\[
E
=
\int_{0}^{T} \{ x(t) ]^2 dt
\tag{1.3.3-1}
\]
また、我々が実際にデータを処理するときはパソコンを使います。つまり、データは離散化されます。\[
E
=
\sum_{j=1}^{N} \{ x(j) ]^2 \Delta t
\quad
\left( N=\frac{T}{\Delta t} \right)
\tag{1.3.3-2}
\]
離散化によってサンプリング間隔Δtの2倍以下の周期を持つ波を捉えることは出来なくなります（サンプリング定理）。
この周期2Δtを周波数としたもの、つまり\( f_s = 1 / 2 \Delta t \)をナイキスト周波数と呼びます。
そのため、実際に捉えられるパワースペクトルの範囲は0≦f≦fsの範囲に限られ、それ以外の成分は誤差として残ることになります。
上記内容を踏まえた上で、パワースペクトルの計算を行う必要があります。 本節の詳細については、次章で詳しく述べることにします。
