スペクトル解析
1．スペクトル
1．1．スペクトルの概念
スペクトルの概念を語るとき、必ずと言ってよいほど出てくるのが“分光スペクトル”です。 太陽光をプリズムに通すと、様々な光の色の帯ができます。 この帯を光の波長順に並べたものが分光スペクトルになります。
図1.1－1 太陽光の分光スペクトルの例
（この図は適当ですので、正確なものは別サイトをご参照ください）
様々な事象にスペクトルの概念を導入する際、この分光スペクトルとの類似性を根拠にすることが多くみられます。
そのため、スペクトルそのものの根源的な意味がはっきりしない、と感じることがあるのではないか？と思います。
そこで、スペクトル（Spectrum）の意味について汎用性（抽象性）を持たせるために、次のように定義してみます。
何らかの変動要素を持つ解析対象は、一般に様々な成分の重ね合わせによって構成される。
その成分をある基準となる量の大小で配列化したものをスペクトルと呼ぶ。
（この文言はwikipedeiaの 「スペクトル」 を参考にさせていただきました）
この定義と分光スペクトルを比較してみると、次のようになります。
表1.1－1 スペクトルと分光スペクトルの比較
| スペクトル | 分光スペクトル |
|---|---|
| 何らかの変動要素をもつ解析対象 | 太陽光 |
| 様々な成分 | 様々な色の光 |
| ある基準となる量の大小で配列化 | 色の帯を波長順に並べたもの |
1．2．データのスペクトル解析
もし、取得したデータが一定の値をとり、何の変化もなければどう思うでしょう？ おそらく、何の興味もわかないのではないでしょうか。 例えば、毎日体重を測っていたとして、暴飲暴食しても、何も飲み食いしなくても体重は変わらずず～っと同じ値を示していたら、体重計に乗ることはなくなるはずです。
図1.2－1 データの変動
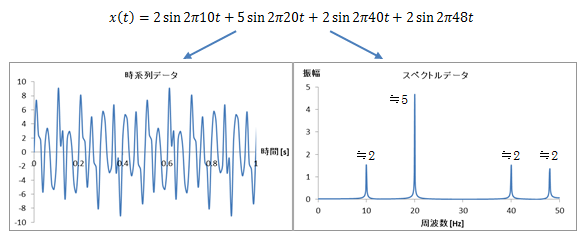
つまり、私たちが興味の対象とするデータには何らかの変動が含まれているはずで、それを前提に話を進めます。 また、データは一般に時間変化に伴い計測されるものですから、時間tの関数=時系列データx(t)を対象にします。ここで、フーリエによって提唱された非常に重要な以下の概念を時系列データに適用します。
任意の周期関数は、三角関数の級数によって展開できる＝フーリエ級数展開
\[
x(t)
=
\frac{a_o}{2}
+ \sum_{n=1}^{\infty} {(a_n \cos 2 \pi f n t + b_n \sin 2 \pi f n t) }
\tag{1.2-1}
\]
三角関数は周期（その逆数である周波数）を持つ“波”を表現し、
その級数の重ね合わせによって時系列データは構成されている、ということを言っています。
つまり、様々な周波数成分を持った波の重ね合わせによって時系列データは構成されている、ということです。
以上の内容をスペクトルの定義と比較すると、次のようになります。- 解析対象
- 時系列データ\( x(t) \)
- 様々な成分
- 様々な周波数を持つ波 \( a_n \cos 2 \pi f n t, b_n \sin 2 \pi f n t \)
- 配列化
- 各周波数成分の振幅an、bnを周波数\( fn \)の大小にあわせて並べたもの
図1.2－2 スペクトル解析の例
ところで、本サイトのスペクトル解析で扱うデータは時系列データに限定していますが、 実際は時間を陽的に含まないデータであってもスペクトル解析は有効な場合が多々あります。 例えば金属表面の面粗さデータなど（時間が位置に代わっています）はこれに該当します。 ですが、実際は金属を加工するのは時間的な進展があって成立するものですから、このデータには時間が陰的に含まれている、と考えることができます。 従ってスペクトル解析は、陽的な時系列データだけでなくもっと幅広く適用することが可能です。
