行列計算ライブラリ(Excel VBA)
数値計算
>
Excel
- 1.行列計算ライブラリの使い方
- 2.行列計算ライブラリの対象
- 3.行列基本操作
- 4.行列基本計算
- 5.ベクトル演算
- 6.数列の作成
- 7.行列の作成
- 8.変換行列
9.スケーリング/ピボッティング
- 10.行列の分解
- 11.連立方程式の解法(直接法)
12.連立方程式の解法(反復法)
- 13.固有値計算
11.連立方程式の解法(直接法)
連立方程式の解法(直接法)に関する使い方を説明します。| 連立方程式の解法(直接法) | ||
|---|---|---|
| FuncMatSimGE(mat1, vec1, Optional pivFlag, Optional plim, Optional rlim) | ガウス消去法 | |
| FuncMatSimGJ(mat1, mat2, Optional pivFlag, Optional plim, Optional rlim) | ガウス・ジョルダン法 | |
| FuncMatSimLU(mat1, mat2, Optional method, Optional pivFlag, Optional plim, Optional rlim) | LU分解 | |
| FuncMatSimInv(mat1, mat2, Optional pivFlag, Optional plim, Optional rlim) | 逆行列利用 | |
| FuncMatSimQR(mat1, vec1, Optional method, Optional pivFlag, Optional plim, Optional rlim) | QR分解法 | |
| CalcMatBackLU(matOut, ByVal matL, ByVal matU, ByVal matB, Optional rankA, Optional rlim) |
前進→後退代入 (連立方程式を解く途中の関数であり、説明省略します) |
|
| CalcMatBack(matOut, ByVal matA, ByVal matB, Optional rankA, Optional rlim) |
後退代入 (連立方程式を解く途中の関数であり、説明省略します) |
|
ガウス消去法
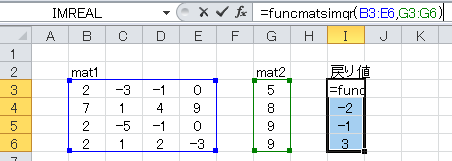
FuncMatSimGE(mat1, vec1, Optional pivFlag, Optional plim, Optional rlim)
| 戻り値 | 連立一次方程式の解(二次配列:ベクトル(行,0))。 |
|---|---|
| mat1 | 係数行列(二次配列)。 |
| vec1 | 定数項ベクトル(二次配列:(行,0)) |
| pivFlag |
前処理フラグ(省略可)。 0=部分行ピボット、1=行ピボット、2=行スケーリング+ピボット、3=完全ピボット、4=スケーリング+完全ピボット |
| plim | ピボット処理閾値(省略可)。デフォルト値=2e-12。 |
| rlim | 数値丸め閾値(省略可)。デフォルト値=2e-12。 |
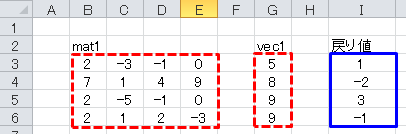
vec1としてセルB3~E6に、vec2にセルG3~G6に、下図のように数値を入力します。
Sub test()
Dim tmp As Variant
Dim mat1 As Variant
Dim vec1 As Variant
’セル値を配列に代入
mat1 = Range("B3:E6").Value
vec1 = Range("G3:G6").Value
’ガウス消去法による連立方程式の解
tmp = FuncMatSimGE(mat1, vec1)
’結果出力
Range("I3:I6").Value = tmp
End Sub
ガウス・ジョルダン法
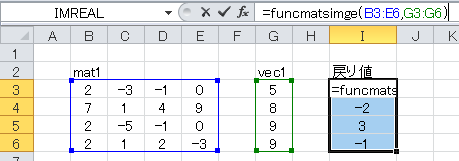
FuncMatSimGJ(mat1, mat2, Optional pivFlag, Optional plim, Optional rlim)
係数行列を共通とする連立方程式(つまり、定数項が異なる)を同時に解くことができます。
ガウス消去法では定数項をベクトルで与えましたが、ガウスジョルダン法では、定数項ベクトルを列ベクトルとする行列で与えることができます。
| 戻り値 | 連立一次方程式の解(二次配列)。 |
|---|---|
| mat1 | 係数行列(二次配列)。 |
| mat2 | 定数項ベクトルを列ベクトルとする行列(二次配列)。 |
| pivFlag |
前処理フラグ(省略可)。 0=部分行ピボット、1=行ピボット、2=行スケーリング+ピボット、3=完全ピボット、4=スケーリング+完全ピボット |
| plim | ピボット処理閾値(省略可)。デフォルト値=2e-12。 |
| rlim | 数値丸め閾値(省略可)。デフォルト値=2e-12。 |
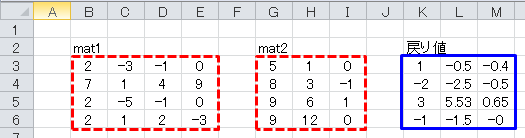
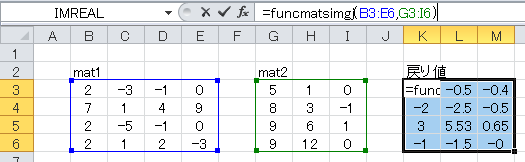
vec1としてセルB3~E6に、vec2にセルG3~I6に、下図のように数値を入力します。 戻り値は、3つの連立方程式の解が3つの列ベクトルとして返されます。
Sub test()
Dim tmp As Variant
Dim mat1 As Variant
Dim mat2 As Variant
’セル値を配列に代入
mat1 = Range("B3:E6").Value
mat2 = Range("G3:I6").Value
’ガウス・ジョルダン法による連立方程式の解
tmp = FuncMatSimGJ(mat1, mat2)
’結果出力
Range(Cells(3, 11), Cells(3 + UBound(tmp, 1), 11 + UBound(tmp, 2))).Value = tmp
End Sub
LU分解
FuncMatSimLU(mat1, mat2, Optional method, Optional pivFlag, Optional plim, Optional rlim)
ガウス消去法とほぼ同じです。
違いは係数行列を共通とする連立方程式(つまり、定数項が異なる)を同時に解くことができます。
ガウス消去法では定数項をベクトルで与えましたが、LU分解法では、定数項ベクトルを列ベクトルとする行列で与えることができます。
| 戻り値 | 連立一次方程式の解(二次配列)。 |
|---|---|
| mat1 | 係数行列(二次配列)。 |
| mat2 | 定数項ベクトルを列ベクトルとする行列(二次配列)。 |
| method |
LU分解方法の指定(省略可)。 0=ガウス消去法(デフォルト)、1=クラウト法 |
| pivFlag |
前処理フラグ(省略可)。 0=部分行ピボット、1=行ピボット、2=行スケーリング+ピボット、3=完全ピボット、4=スケーリング+完全ピボット |
| plim | ピボット処理閾値(省略可)。デフォルト値=2e-12。 |
| rlim | 数値丸め閾値(省略可)。デフォルト値=2e-12。 |
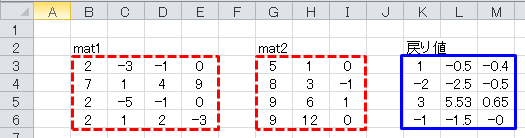
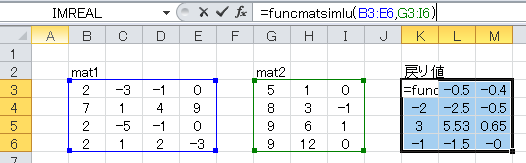
vec1としてセルB3~E6に、vec2にセルG3~I6に、下図のように数値を入力します。 戻り値は、3つの連立方程式の解が3つの列ベクトルとして返されます。
Sub test()
Dim tmp As Variant
Dim mat1 As Variant
Dim mat2 As Variant
’セル値を配列に代入
mat1 = Range("B3:E6").Value
mat2 = Range("G3:I6").Value
’LU分解法による連立方程式の解
tmp = FuncMatSimLU(mat1, mat2)
’結果出力
Range(Cells(3, 11), Cells(3 + UBound(tmp, 1), 11 + UBound(tmp, 2))).Value = tmp
End Sub
逆行列利用
FuncMatSimInv(mat1, mat2, Optional pivFlag, Optional plim, Optional rlim)
数値計算では通常、逆行列を用いた連立方程式の解法を用いません(計算不安定性など)。
| 戻り値 | 連立一次方程式の解(二次配列)。 |
|---|---|
| mat1 | 係数行列(二次配列)。 |
| mat2 | 定数項ベクトルを列ベクトルとする行列(二次配列)。 |
| pivFlag |
前処理フラグ(省略可)。 0=部分行ピボット、1=行ピボット、2=行スケーリング+ピボット、3=完全ピボット、4=スケーリング+完全ピボット |
| plim | ピボット処理閾値(省略可)。デフォルト値=2e-12。 |
| rlim | 数値丸め閾値(省略可)。デフォルト値=2e-12。 |
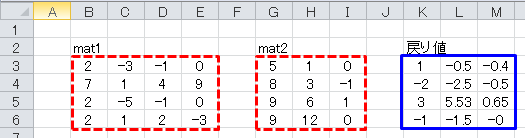
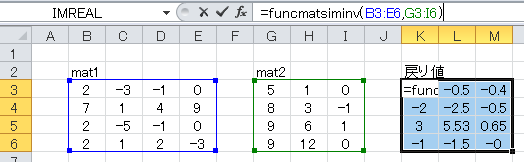
vec1としてセルB3~E6に、vec2にセルG3~I6に、下図のように数値を入力します。 戻り値は、3つの連立方程式の解が3つの列ベクトルとして返されます。
Sub test()
Dim tmp As Variant
Dim mat1 As Variant
Dim mat2 As Variant
’セル値を配列に代入
mat1 = Range("B3:E6").Value
mat2 = Range("G3:I6").Value
’逆行列法による連立方程式の解
tmp = FuncMatSimInv(mat1, mat2)
’結果出力
Range(Cells(3, 11), Cells(3 + UBound(tmp, 1), 11 + UBound(tmp, 2))).Value = tmp
End Sub
QR分解法
FuncMatSimQR(mat1, vec1, Optional method, Optional pivFlag, Optional plim, Optional rlim)
| 戻り値 | 連立一次方程式の解(二次配列:(行,0))。 |
|---|---|
| mat1 | 係数行列(二次配列)。 |
| vec1 | 定数項ベクトル(二次配列:(行,0))。 |
| method |
QR分解方法の指定(省略可)。 0=ハウスホルダー法(デフォルト)、1=グラムシュミット法。 |
| pivFlag |
前処理フラグ(省略可)。 0=部分行ピボット、1=行ピボット、2=行スケーリング+ピボット |
| plim | ピボット処理閾値(省略可)。デフォルト値=2e-12。 |
| rlim | 数値丸め閾値(省略可)。デフォルト値=2e-12。 |
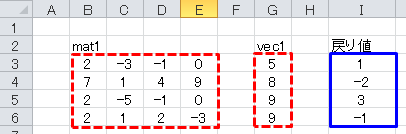
vec1としてセルB3~E6に、vec2にセルG3~G6に、下図のように数値を入力します。 戻り値は、3つの連立方程式の解が3つの列ベクトルとして返されます。
Sub test()
Dim tmp As Variant
Dim mat1 As Variant
Dim mat2 As Variant
’セル値を配列に代入
mat1 = Range("B3:E6").Value
mat2 = Range("G3:G6").Value
’QR法による連立方程式の解
tmp = FuncMatSimQR(mat1, mat2)
’結果出力
Range(Cells(3, 9), Cells(3 + UBound(tmp, 1), 9 + UBound(tmp, 2))).Value = tmp
End Sub