gijyutsu-keisan.com

10．行列の分解（LU分解、QR分解）

10．1．LU分解

LU分解に関する使い方を説明します。
LU分解
FuncMatLUCrout(mat1, Optional pivFlag, Optional plim, Optional rlim, Optional outFlag) LU分解：クラウト法
FuncMatLUGE(mat1, Optional pivFlag, Optional plim, Optional rlim, Optional outFlag) LU分解：ガウス消去法
FuncMatCholesky(mat1, Optional rlim) LU分解：修正コレスキー分解
FuncMatIcCholesky(mat1, Optional slim) LU分解：不完全コレスキー分解

LU分解：クラウト法

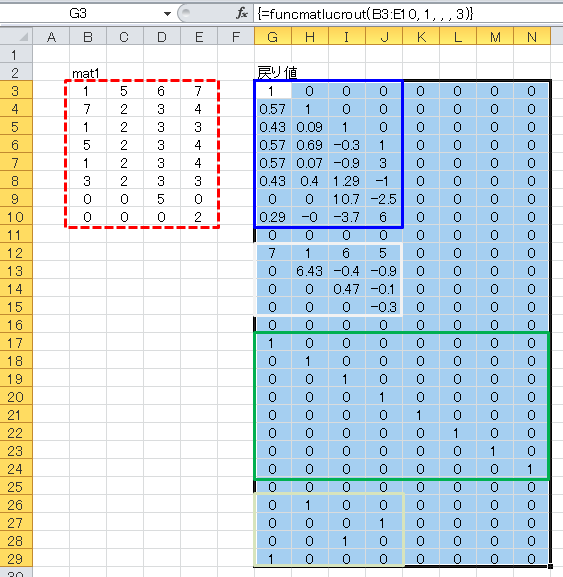
FuncMatLUCrout(mat1, Optional pivFlag, Optional plim, Optional rlim, Optional outFlag)
クラウト法を用いたLU分解を行います。
戻り値 ジャグ配列または二次配列で結果を出力。
二次配列の場合、上から下三角行列L、上三角行列U、行前処理行列Pr、列前処理行列Pc。
ジャグ配列の場合、(0)(行,列）=下三角行列、(1)(行,列）=上三角行列、(2)(行,列）=行前処理行列、(3)(行,列）=列前処理行列
mat1 LU分解対象行列（行,列）。
正方行列以外にも対応しています。
pivFlag 前処理フラグ（省略可）。
0=部分行ピボット、1=行ピボット、2=行スケーリング＋ピボット、3=完全ピボット、4=スケーリング＋完全ピボット
plim ピボット処理閾値（省略可）。デフォルト値=2e-12。
rlim 数値丸め閾値（省略可）。デフォルト値=2e-12。
aryFlag 前処理行列の出力方法。
0=ジャグ配列 + 変換行列連立方程式用（デフォルト）。
1=ジャグ配列 + 変換行列分解確認用。
2=1つの配列にまとめて出力 + 変換行列連立方程式用。
3=1つの配列にまとめて出力 + 変換行列分解確認用。
引数の指定方法例を紹介しておきます。
  1. 部分行ピボットでLU分解する場合（通常はこの方法で使用します）
    FuncMatLUCrout(mat1)
  2. 完全ピボットでLU分解する場合
    FuncMatLUCrout(mat1,3)
  3. ピボット処理判定値を1e-6として、完全ピボットでLU分解する場合
    FuncMatLUCrout(mat1,3,1e-6)
  4. 出力（aryFlag）を二次配列、変換行列の逆行列を出力する場合
    FuncMatLUCrout(mat1,,,,3)

    5. VBAサンプルは次の通りです。 
    Sub test2()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’クラウト法によるLU分解
tmp = FuncMatLUCrout(matA, 1, , , 3)

’結果出力（ジャグ配列）
cntR1 = 3
cntC1 = 11
For cnt1 = 0 To UBound(tmp)
cntR2 = cntR1 + UBound(tmp(cnt1), 1)
cntC2 = cntC1 + UBound(tmp(cnt1), 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp(cnt1)
cntR1 = cntR2 + 2
Next cnt1

End Sub
    二次配列として返す場合は次のように書きます。 
    Sub test3()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’クラウト法によるLU分解
tmp = FuncMatLUCrout(matA, 1, , , 3)

’結果出力（二次配列）
cntR1 = 3
cntC1 = 11
cntR2 = cntR1 + UBound(tmp, 1)
cntC2 = cntC1 + UBound(tmp, 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp

End Sub
    FuncMatLUCroutは、二次配列で返す場合、Excel関数としても使えます（この場合、aryFlag=2または3とします）。
    なお、Functionプロシージャを用いると、出力操作等計算には不必要な処理が入るため、効率的に計算を進めたい場合は、Functionプロシージャ内で指示されているSubプロシージャ
    CalcMatLUCrout(matL, matU, matPr, matPc, rankA, ByVal matA, Optional pivFlag, Optional plim, Optional rlim, Optional outFlag)
    の使用をお勧めします。

LU分解：ガウス消去法

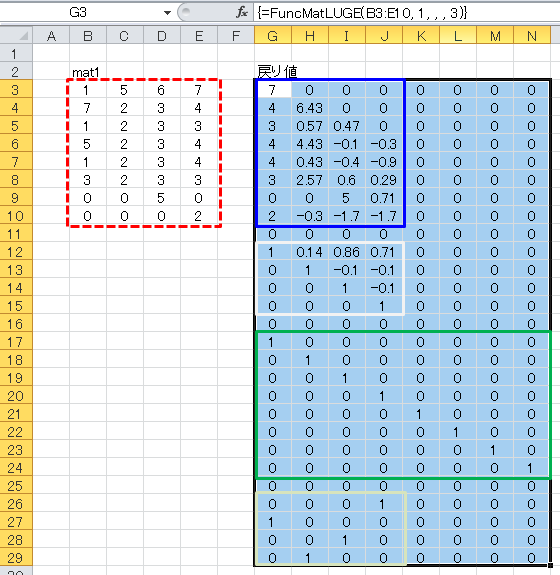
FuncMatLUGE(mat1, Optional pivFlag, Optional plim, Optional rlim, Optional aryFlag)
ガウス消去法を用いたLU分解を行います。
戻り値 ジャグ配列または二次配列で結果を出力。
二次配列の場合、上から下三角行列L、上三角行列U、行前処理行列Pr、列前処理行列Pc。
ジャグ配列の場合、(0)(行,列）=下三角行列、(1)(行,列）=上三角行列、(2)(行,列）=行前処理行列、(3)(行,列）=列前処理行列
mat1 LU分解対象行列（行,列）。
正方行列以外にも対応しています。
pivFlag 前処理フラグ（省略可）。
0=部分行ピボット、1=行ピボット、2=行スケーリング＋ピボット、3=完全ピボット、4=スケーリング＋完全ピボット
plim ピボット処理閾値（省略可）。デフォルト値=2e-12。
rlim 数値丸め閾値（省略可）。デフォルト値=2e-12。
aryFlag 前処理行列の出力方法。
0=ジャグ配列 + 変換行列連立方程式用（デフォルト）。
1=ジャグ配列 + 変換行列分解確認用。
2=1つの配列にまとめて出力 + 変換行列連立方程式用。
3=1つの配列にまとめて出力 + 変換行列分解確認用。
引数の指定方法例を紹介しておきます。
  1. 部分行ピボットでLU分解する場合（通常はこの方法で使用します）
    FuncMatLUGE(mat1)
  2. 完全ピボットでLU分解する場合
    FuncMatLUGE(mat1,3)
  3. ピボット処理判定値を1e-6として、完全ピボットでLU分解する場合
    FuncMatLUGE(mat1,3,1e-6)
  4. 出力（aryFlag）を二次配列、変換行列の逆行列を出力する場合
    FuncMatLUGE(mat1,,,,3)
    5. VBAサンプルは次の通りです。 
    Sub test2()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’ガウス消去法によるLU分解
tmp = FuncMatLUGE(matA, 1, , , 1)

’結果出力（ジャグ配列）
cntR1 = 3
cntC1 = 11
For cnt1 = 0 To UBound(tmp)
cntR2 = cntR1 + UBound(tmp(cnt1), 1)
cntC2 = cntC1 + UBound(tmp(cnt1), 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp(cnt1)
cntR1 = cntR2 + 2
Next cnt1

End Sub
    二次配列として返す場合は次のように書きます。 
    Sub test3()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’ガウス消去法によるLU分解
tmp = FuncMatLUGE(matA, 1, , , 3)

’結果出力（二次配列）
cntR1 = 3
cntC1 = 11
cntR2 = cntR1 + UBound(tmp, 1)
cntC2 = cntC1 + UBound(tmp, 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp

End Sub
    FuncMatLUGEは、二次配列で返す場合、Excel関数としても使えます（この場合、aryFlag=2または3とします）。
    なお、Functionプロシージャを用いると、出力操作等計算には不必要な処理が入るため、効率的に計算を進めたい場合は、Functionプロシージャ内で指示されているSubプロシージャ
    CalcMatLUGE(matL, matU, matPr, matPc, rankA, ByVal matA, Optional pivFlag, Optional plim, Optional rlim, Optional outFlag)
    の使用をお勧めします。

QR分解：グラムシュミット法

FuncMatQRGS(mat1, Optional aryFlag)
グラムシュミット法を用いたQR分解を行います。
一般に、数値計算プログラムでQR分解を利用する場合は、次のハウスホルダー法を用います。 グラム・シュミット法はあまり使用されません。
戻り値 ジャグ配列または二次配列で結果を出力。
二次配列の場合、上からユニタリ行列Q、上三角行列R。
ジャグ配列の場合、(0)(行,列）=ユニタリ行列Q、(1)(行,列）=上三角行列R。
mat1 QR分解対象行列（二次配列）。
aryFlag 前処理行列の出力方法。
0=ジャグ配列。
2=1つの配列にまとめて出力。

VBAサンプルは次の通りです。 
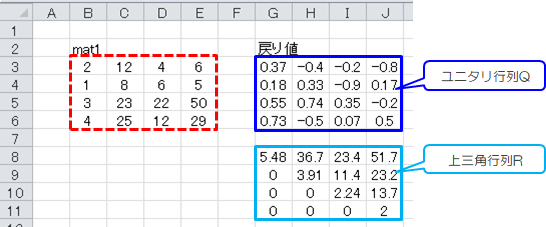
Sub test2()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’グラムシュミット法によるQR分解
tmp = FuncMatQRGS(matA, 0)

’結果出力（ジャグ配列）
cntR1 = 3
cntC1 = 7
For cnt1 = 0 To UBound(tmp)
cntR2 = cntR1 + UBound(tmp(cnt1), 1)
cntC2 = cntC1 + UBound(tmp(cnt1), 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp(cnt1)
cntR1 = cntR2 + 2
Next cnt1

End Sub
二次配列として返す場合は次のように書きます。 
Sub test3()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’グラムシュミット法によるQR分解
tmp = FuncMatQRGS(matA, 2)

’結果出力（二次配列）
cntR1 = 3
cntC1 = 7
cntR2 = cntR1 + UBound(tmp, 1)
cntC2 = cntC1 + UBound(tmp, 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp

End Sub

QR分解：ハウスホルダー法

FuncMatQRHH(mat1, Optional pivFlag, Optional plim, Optional rlim, Optional aryFlag)
ハウスホルダー法を用いたQR分解を行います。
数値計算でのQR分解と言えば、一般にこのハウスホルダー法のことを指します。
戻り値 ジャグ配列または二次配列で結果を出力。
二次配列の場合、上からユニタリ行列Q、上三角行列R、列前処理行列Pc。
ジャグ配列の場合、(0)(行,列）=ユニタリ行列Q、(1)(行,列）=上三角行列R、(2)(行,列）=列前処理行列Pc。
mat1 QR分解対象行列（二次配列）。
行数≧列数を満たせば、正方行列でなくても構いません。
pivFlag 前処理フラグ（省略可）。
0=部分列ピボット、1=列スケーリング＋ピボット
plim ピボット処理閾値（省略可）。デフォルト値=2e-12。
rlim 数値丸め閾値（省略可）。デフォルト値=2e-12。
aryFlag 前処理行列の出力方法。
0=ジャグ配列 + 変換行列連立方程式用（デフォルト）。
1=ジャグ配列 + 変換行列分解確認用。
2=1つの配列にまとめて出力 + 変換行列連立方程式用。
3=1つの配列にまとめて出力 + 変換行列分解確認用。
引数の指定方法例を紹介しておきます。
  1. 部分列ピボットでQR分解する場合（通常はこの方法で使用します）
    FuncMatQRHH(mat1)
  2. スケーリング+列ピボットでQR分解する場合
    FuncMatQRHH(mat1,3)
  3. ピボット処理判定値を1e-6として、完全ピボットでLU分解する場合
    FuncMatQRHH(mat1,3,1e-6)
  4. 出力（aryFlag）を二次配列、ユニタリ行列Qと変換行列の逆行列を出力する場合
    FuncMatQRHH(mat1,,,,3)
    5. VBAサンプルは次の通りです。 
    Sub test2()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’ハウスホルダー法によるQR分解
tmp = FuncMatQRHH(matA, , , , 1)

’結果出力（ジャグ配列）
cntR1 = 3
cntC1 = 7
For cnt1 = 0 To UBound(tmp)
cntR2 = cntR1 + UBound(tmp(cnt1), 1)
cntC2 = cntC1 + UBound(tmp(cnt1), 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp(cnt1)
cntR1 = cntR2 + 2
Next cnt1

End Sub
    二次配列として返す場合は次のように書きます。 
    Sub test3()

Dim cnt1 As Integer
Dim cntC1 As Integer, cntC2 As Integer
Dim cntR1 As Integer, cntR2 As Integer

Dim tmp As Variant
Dim matA As Variant

’行列の取得
cntR1 = 3
cntC1 = 2
cntR2 = Cells(cntR1, cntC1).End(xlDown).Row
cntC2 = Cells(cntR1, cntC1).End(xlToRight).Column
matA = Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value

’ハウスホルダー法によるQR分解
tmp = FuncMatQRHH(matA, , , , 3)

’結果出力（二次配列）
cntR1 = 3
cntC1 = 7
cntR2 = cntR1 + UBound(tmp, 1)
cntC2 = cntC1 + UBound(tmp, 2)
Range(Cells(cntR1, cntC1), Cells(cntR2, cntC2)).Value = tmp

End Sub
    FuncMatQRHHは、二次配列で返す場合、Excel関数としても使えます（この場合、aryFlag=2または3とします）。
    なお、Functionプロシージャを用いると、出力操作等計算には不必要な処理が入るため、効率的に計算を進めたい場合は、Functionプロシージャ内で指示されているSubプロシージャ
    CalcMatQRHH(matQ, matR, matPc, ByVal matA, Optional pivFlag, Optional plim, Optional rlim, Optional outFlag)
    の使用をお勧めします。

参考文献

▲