固有値計算
1.固有値計算
1.1.固有値計算法
ここでは、数値計算によって固有値、固有ベクトルを計算する方法について見ていきます。まずは固有値とその特徴について確認します。
<固有値の定義>
\[ A \boldsymbol{ x_i } = \lambda \boldsymbol{ x_i } \ \land \ \boldsymbol{ x_i } \neq \boldsymbol{ o } \tag{1-1} \] を満たす\( \lambda_i \)をAの固有値、\( \boldsymbol{ x_i } \)を\( \lambda_i \)に属するAの固有ベクトルと呼びます。 また、\( \lambda_i \) 、\( \boldsymbol{ x_i } \)をまとめてAの固有対と呼びます。固有値は次の性質を満たします。
- 相似変換\( P \)に対して固有値は不変(\( P \)は正則)
\[ \det ( P^{-1} A P - \lambda I ) = \det( A - \lambda I ) \] - \( P^(-1) A P = R \)(上三角行列)のとき、\( A \)の固有値は\( R \)の対角成分
- \( A \boldsymbol{ x_i } = \lambda_i \boldsymbol{ x_i } \Longleftrightarrow A^{-1} \boldsymbol{ x_i } = \frac{ 1 }{ \lambda_i } \boldsymbol{ x_i } \)
- \( A \boldsymbol{ x_i } = \lambda_i \boldsymbol{ x_i } 、|\lambda_1 | \geq |\lambda_2 | \geq \ldots \geq |\lambda_n | \)のとき、\( \boldsymbol{ v } = c_1 \boldsymbol{ x_1 } + \ldots + c_n \boldsymbol{ x_n } = \boldsymbol{ v^{ (0) }} \ \)として、\( \boldsymbol{ v^{(k+1)} } = A \boldsymbol{ v^{(k)} } \ \)を\( k \)に対して∞回繰り返し計算すれば、
\[ \frac{ \boldsymbol{ v^{(k+1)} } \cdot \boldsymbol{ v^{(k)} } } { \boldsymbol{ v^{(k)} } \cdot \boldsymbol{ v^{(k)} } } \ \rightarrow \ \lambda , \quad \boldsymbol{ v^{(k)} } \ \rightarrow \ \boldsymbol{ x } \]
固有値計算の主な方法として、次のようなものが挙げられます。
1.2.相似変換に用いる行列
1.2.1.相似変換
相似変換とは次のようなものです。
n次正方行列A、B、可逆行列Pがあって、
\[
P^{-1} A P = B
\tag{1.2.1-1}
\]
の関係があるとき、次の3つの性質を満足するものを相似変換と呼びます。
この相似変換\( P^{-1} A P \)によってAの固有値が不変であることは、次で証明できます。
- 反射:A~A
- 対称:A~B⇒B~A
- 推移:A~B,B~C⇒A~C
\[
\begin{eqnarray}
& \det{ ( \lambda I - P^{-1} A P ) }
\quad
& =
\det{ ( \lambda P^{-1} I P - P^{-1} A P ) }
\\
& & =
\det{ ( P^{-1} ( \lambda I - A ) P ) }
\\
& & =
\det{ ( P^{-1} ) }\det{ ( \lambda I - A ) }\det{ ( P ) }
\\
& & =
\det{ ( \lambda I - A ) }
\tag{1.2.1-2}
\end{eqnarray}
\]
\[
( \because \det{ ( P^{-1} ) } = 1 / \det{ ( P ) } )
\]
1.2.2.基本変形行列
基本変形行列として次の3つがあります(詳細は線型代数ページにゆずります)。- \( i \)行(列)と\( j \)行(列)の交換:
単位行列\( I \)の\( i \)行\( i \)列と\( j \)行\( j \)列成分を、\( i \)行\( j \)列と\( j \)行\( i \)列成分と入れ替えたもの
\[ P(i,j) = \begin{pmatrix} & 1 & & \vdots & & \vdots & & & \\ & & \ddots & \vdots & & \vdots & & & \\ & \cdots & \cdots & 0 & \cdots & 1 & \cdots & \cdots & \\ & & & \vdots & \ddots & \vdots & & & \\ & \cdots & \cdots & 1 & \cdots & 0 & \cdots & \cdots & \\ & & & \vdots & & \vdots & \ddots & & \\ & & & \vdots & & \vdots & & 1 & \end{pmatrix} \] - \( i \)行(列)の\( c \)倍:
単位行列\( I \)の\( i \)行\( i \)列を\( c \)倍したもの
\[ M(i,j) = \begin{pmatrix} & 1 & & & \vdots & & & & \\ & & \ddots & & \vdots & & & & \\ & & & 1 & \vdots & & & & \\ & \cdots & \cdots & \cdots & c & \cdots & \cdots & \cdots & \\ & & & & \vdots & 1 & & & \\ & & & & \vdots & & \ddots & & \\ & & & & \vdots & & & 1 & \end{pmatrix} \] - \( i \)行(列)の\( c \)倍:
\( j \)行(列)を\( c \)倍して\( i \)行(列)に加える
\[ A(i,j;c) = \begin{pmatrix} & 1 & & \vdots & & & & & \\ & & \ddots & \vdots & & & & & \\ & & & 1 & & & & & \\ & & & \vdots & \ddots & & & & \\ & \cdots & \cdots & c & \cdots & 1 & \cdots & \cdots & \\ & & & \vdots & & \vdots & \ddots & & \\ & & & \vdots & & \vdots & & 1 & \end{pmatrix} \]
行列\( A \)に対し、相似変換行列\( T \)を左から掛けると行変換、右から掛けると列変換になります。
- 行変換: \[ T A = \begin{pmatrix} & 0 & 1 & 0 & \\ & 1 & 0 & 0 & \\ & 0 & 0 & 1 & \end{pmatrix} \begin{pmatrix} & \txc{blue}{ a } & \txc{blue}{ b } & \txc{blue}{ c } & \\ & \txc{red}{ d } & \txc{red}{ e } & \txc{red}{ f } & \\ & g & h & i & \end{pmatrix} = \begin{pmatrix} & \txc{red}{ d } & \txc{red}{ e } & \txc{red}{ f } & \\ & \txc{blue}{ a } & \txc{blue}{ b } & \txc{blue}{ c } & \\ & g & h & i & \end{pmatrix} \]
- 列変換: \[ A T = \begin{pmatrix} & \txc{blue}{ a } & \txc{red}{ b } & c & \\ & \txc{blue}{ d } & \txc{red}{ e } & f & \\ & \txc{blue}{ g } & \txc{red}{ h } & i & \end{pmatrix} \begin{pmatrix} & 0 & 1 & 0 & \\ & 1 & 0 & 0 & \\ & 0 & 0 & 1 & \end{pmatrix} = \begin{pmatrix} & \txc{red}{ b } & \txc{blue}{ a } & c & \\ & \txc{red}{ e } & \txc{blue}{ d } & f & \\ & \txc{red}{ h } & \txc{blue}{ g } & i & \end{pmatrix} \]
1.2.3.ギブンス行列
ギブンス変換は次式で定義される相似変換行列です。 主に4章でみるQR分解で用います。
\[
G(i,j,\theta)
=
\begin{pmatrix}
& 1 & 0 & & \cdots & & \cdots & 0 &
\\
& 0 & \ddots & \vdots & & \vdots & & \vdots &
\\
& & \cdots & \cos{\theta} & \cdots & \sin{\theta} & \cdots & &
\\
& \vdots & & \vdots & \ddots & \vdots & & \vdots &
\\
& & \cdots & -\sin{\theta} & \cdots & \cos{\theta} & \cdots & &
\\
& \vdots & & \vdots & & \vdots & \ddots & 0 &
\\
& 0 & \cdots & & \cdots & & 0 & 1 &
\end{pmatrix}
\]
この定義から、\( G^{-1} = G^t \)、\( \det{G} = 1 \)となることから、ユニタリ行列になります。
また、ギブンス変換には平面内の回転変換の意味があります
(二次元の回転行列を思い浮べてもらえば、同じ形をしていることがわかります)。
さて、ギブンス変換を実際に計算してみると、次のようになります (\( c = \cos{\theta}, s = \sin{\theta} \)とします)。
\[
\begin{array}{1}
\begin{pmatrix}
& 1 & 0 & 0 & 0 &
\\
& 0 & c & 0 & s &
\\
& 0 & 0 & 1 & 0 &
\\
& 0 & -s & 0 & c &
\end{pmatrix}
\begin{pmatrix}
& a_{11} & a_{12} & a_{13} & a_{14} &
\\
& a_{21} & a_{22} & a_{23} & a_{24} &
\\
& a_{31} & a_{32} & a_{33} & a_{34} &
\\
& a_{41} & a_{42} & a_{43} & a_{44} &
\end{pmatrix}
\\
\\
=
\begin{pmatrix}
& a_{11} & a_{12} & a_{13} & a_{14} &
\\
& a_{21} c + a_{41}s & a_{22}c + a_{42}s & a_{23}c + a_{43}s & a_{24}c + a_{44}s &
\\
& a_{31} & a_{32} & a_{33} & a_{34} &
\\
& \txc{red}{-a_{21}s + a_{41}c} & -a_{22}s + a_{42}c & -a_{23}s + a_{43}c & -a_{24}s + a_{44}c &
\end{pmatrix}
\end{array}
\]
この計算方法から、ギブンス変換の\( \theta \)を行列\( A \)の要素を使って定義することで、狙った要素を0にすることが可能です。
例えば、4行1列目の成分(上行列の赤文字要素)を0にするためには次のように設定すればよいことになります。
\( r = \sqrt { a_{21}^2 + a_{41}^2 } \ \)とおいて、 \( c = \cos{\theta} = \displaystyle\frac{a_{21}}{r}, \ s = \sin{\theta} = \displaystyle\frac{a_{41}}{r} \)
1.2.4.ハウスホルダー行列
ハウスホルダー変換は別名“鏡像変換”とも呼ばれ、次の原理に基いています。まず、次のようにパラメータを設定します。
- 空間上の任意の点\( \bf{ x } \)
- 原点を含む平面Uの法線ベクトル\( \bf{ u } \)
(\( \bf{ u u^{t} } = \bf{ u u^{t} } \otimes \bf{ u u^{t} } \)は正方行列になります)
点\( \bf{ x' } \)と\( \bf{ x } \)を結ぶ直線は \[ \bf{ x } - \bf{ x' } = \bf{ x } - ( I - 2 \bf{ u u^{t} } ) \bf{ x } = 2 \bf{ u u^{t} } \bf{ x } \tag{1.2.3-2} \] で表せます。 ここで\( \bf{ u^{t} } \bf{ x } \)はベクトル\( \bf{ u } \)と\( \bf{ x } \)の内積であるため、\( \bf{ u u^{t} } \bf{ x } \)は \( \bf{ u } \)のスカラー倍、つまり\( \bf{ x } - \bf{ x' } \)は \( \bf{ u } \)と平行であることがわかります。 さらに、\( \bf{ u } \)と\( \bf{ x } - \bf{ u u^{t} x } \)の内積を計算すると、
\[
\bf{ u } \cdot ( \bf{ x } - \bf{ u u^{t} x } )
=
\bf{ u^t } \bf{ x } - \bf{ u^t u u^{t} x }
= \bf{ u^t } \bf{ x } - \bf{ u^{t} x }
= 0
\\
\qquad ( \because \bf{ u^t u } = 1 )
\tag{1.2.3-3}
\]
が得られます。
この式から平面Uの法線ベクトル\( \bf{ u } \)と\( \bf{ x } - \bf{ u u^{t} x } \)は直交しており、その結果、点\( \bf{ u u^{t} x } \)(下図中の点M)は平面U内にあることがわかります。
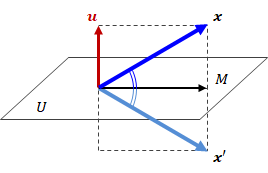
さらに、(1.2.3-2)式の係数2を考慮すれば、「点\( \bf{ x' } \)は点\( \bf{ x } \)の平面Uに対して対称な点」であることがわかります。
従って、(1.2.3-1)式の係数行列 を\( H \)とおいて、
\[
H
=
I - 2 \bf{ u u^{t} }
=
\begin{pmatrix}
& 1 - 2 u_1^2 & -2 u_1u_2 & \cdots & -2 u_1 u_n &
\\
& -2 u_2u_1 & 1 - 2 u_2^2 & \cdots & -2 u_2 u_n &
\\
& \vdots & \vdots & \ddots & \vdots &
\\
& -2 u_n u_1 & -2 u_nu_2 & \cdots & 1 - 2 u_n^2 &
\end{pmatrix}
\tag{1.2.3-4}
\]
をハウスホルダー変換または鏡像変換と呼び、\( H \)で表します。
定義式から\( H \)は明らかに対称行列です。
また\( H \)がユニタリ変換であることは、次の理由からわかります。
- 鏡像の鏡像は元に戻るため、\( H^{-1} = H \leftrightarrow H H = I \)
- \( H^t = I^t - ( \bf{ u u^t } )^t = I - ( \bf{ u u^t } ) = H \)であること(1)から\( H^t = H^{-1} \)
- (1)から\( 1 = \det{ ( H H ) } = \det{ H } \det{ H } \) \( \rightarrow \det{ H } = \pm 1\)
- \( \alpha \neq 0 \)のとき、\( H = I - \bf{u} \bf{u^t} \)
- \( s = 0 \)のとき、\( H = I \)
- \( s = a_{kk} \)のとき、\( \alpha = 0 \)なので計算不能
この変換は主に、4章でみるQR分解で用います。
ハウスホルダー変換もギブンス変換同様、行列\( A \)の要素を使って定義することで、狙った要素を0にすることが可能です。 例えば行列\( A \)
\[
A
=
\begin{pmatrix}
& a_{11} & a_{12} & a_{13} & a_{14} &
\\
& a_{21} & a_{22} & a_{23} & a_{24} &
\\
& a_{31} & \txc{red}{ a_{32} } & a_{33} & a_{34} &
\\
& a_{41} & \txc{red}{ a_{42} } & a_{43} & a_{44} &
\end{pmatrix}
\]
に対して、赤文字部分(2列目の下三角要素)を0にする場合は、ハウスホルダー変換行列の要素を次のように定義します。
\[
\begin{eqnarray}
\left \{
\begin{array}{1}
s
=
\mathrm{ -sgn } \left( a_{22} \ \right)
\displaystyle \sqrt { \sum_{j=2}^{4} a_{jk}^2 }
\quad ( sgn:a_{22}の符号 )
\\
\alpha
=
\sqrt { s \ ( s - a_{22} \ ) }
\end{array}
\right.
\end{eqnarray}
\]
これらを計算してベクトル\( \bf{ u } \)を次のように定義します。
\[ \bf{ u } = \left( \begin{array}{c} 0 \\ s-a_{22} \\ a_{32} \\ a_{42} \end{array} \right) \] ただし、次の条件で場合分けが必要になります。


