ニュートン法
ニュートン法は、関数化された方程式の解を、数値計算によって近似的に求める方法です
(ニュートン・ラフソン法とも呼びます)。
幾何学的に言えば「曲線の交点を求める方法」とも言えます。
ニュートン法は、一変数関数\( f(x) \)でも多変数関数\( f(x_1,x_2,・・・,x_n) \)でも、どちらにも適用できます。
まずはニュートン法のロジックを理解するために、簡単な一変数関数から話を進めます。
Excelによるニュートン法の計算方法については、 Excelによるニュートン法の計算 で説明します(VBAを利用しています)。
まずはニュートン法のロジックを理解するために、簡単な一変数関数から話を進めます。
Excelによるニュートン法の計算方法については、 Excelによるニュートン法の計算 で説明します(VBAを利用しています)。
1.一変数のニュートン法
1.1.一変数のニュートン法手順
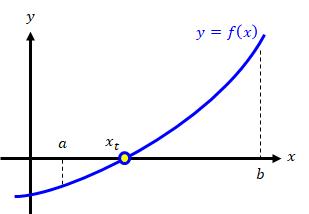
関数\( y=f(x) \)が与えられたとき、ニュートン法を用いて\( f(x)=0 \)の解を求める手順を示します。 これは、関数\( y=f(x) \)と\( y=0 \)の二つの曲線の交点を求めることに他なりません。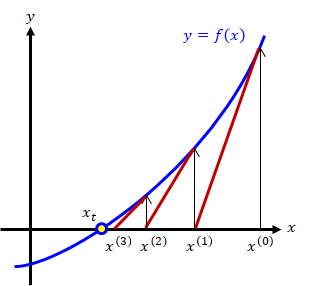
図1-1 ニュートン法の計算
上図と一緒に各Stepの内容を確認してください。Step1:
\( f(x)=0 \)の真の解\( x_t \)の近傍点\( x^{(0)} \ \)を適当に決めます (\( x_t \)は未知なので\( y=f(x) \)をグラフ化してを決めるのが妥当です)。Step2:
点\( ( x^{(0)} , f(x^{(0)} \ ) ) \)での\( f(x) \)の接線を求め、その接線とx軸との交点を\( x^{(1)} \ \)とします。 接線は\( f(x) \)を\( x^{(0)} \)でテイラー展開し、その一次近似をとることで決まります。\[
y = f(x^{(0)}) + f'(x^{(0)}) \ ( x - x^{(0)} )
\tag{1.1-1}
\]
さらに、上式から\( x^{(1)} \ \)が求まります。
\[
x^{(1)} = x^{(0)} - \frac{ f(x^{(0)}) }{ f'(x^{(0)}) }
\tag{1.1-2}
\]
Step3:
前Stepとの解の変化が微小値\( \epsilon \)(収束判定値)より小さければ、\( x^{(1)} \ \)を\( f(x)=0 \)の近似解とします。\[
| x^{(1)} - x^{(0)} | < \epsilon
\tag{1.1-3}
\]
上式を満たさない場合は、解の変化が\( \epsilon \)より小さくなるまで、\( x^{(2)},x^{(3)},\cdots \)を求めて差分を評価する操作、Step2、Step3、・・・を繰り返します。
\[
x^{(i+1)} = x^{(i)} - \frac{ f(x^{(i)}) }{ f'(x^{(i)}) }
\tag{1.1-4}
\]
\[
| x^{(i+1)} - x^{(i)} | < \epsilon
\tag{1.1-5}
\]
なお、収束判定値を小さくするほど真の解\( x_t \)に近づきますが、その分計算回数は増えます。
また、ニュートン法を適用できる関数の条件としては“\( f(x) \)は微分可能”、“計算対象範囲で\( f''(x) \)の符号は一定”の二つです。
1.2.ニュートン法を使った例
(1)“\( \sqrt{2} \ \)”の計算
一般的な例ではありますが、“\( \sqrt{2} \ \)”を計算してみます。まず、関数として
\[
f(x) = x^2 - 2
\]
を準備します。この関数とx軸との交点を求めれば、つまり\( f(x) = 0 \)の解が\( \sqrt{2} \ \)となります。
(1.1-4)式を見ると、\( f(x) \)の一階微分が必要になります。
\[
f'(x) = 2x
\]
ここで初期解\( x^{(0)} = 1 \)をとしてみると、
\[
\begin{eqnarray}
& x^{(1)} & = 1 - \frac{-1}{2} = 1.5
\\
& x^{(2)} & = 1.5 - \frac{ 0.25 }{ 3} = 1.41666\cdots
\end{eqnarray}
\]
という風になり、例えば計算を4回繰り返せば
\[
x^{(4)} = 1.4142135623\cdots
\]
が得られます。
(2)“\( x^2 - 4 = 0 \)”の計算
(1)の例とほとんど同じですが、ここでは初期値を変えることによる影響を見ていきます。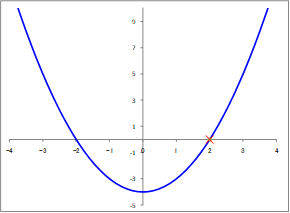 上図3-1からもわかるように、\( f(x)=0 \)の解はx=±2になります。
上図3-1からもわかるように、\( f(x)=0 \)の解はx=±2になります。
ここで、初期値\( x^{(0)} = 3 \)として計算してみると、反復計算5回目で“x=+2”という解を得ることができます。
表1.3-1 \( x_0 = 3 \)での\( f(x)=0 \)の解

次に、初期値\( x^{(0)} = -3 \)として計算してみると、反復計算5回目で“x=-2”という解を得ることができます。
表1.3-2 \( x_0 = -3 \)での\( f(x)=0 \)の解
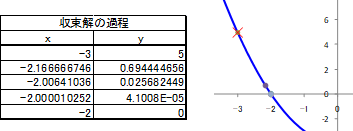 最後に、初期値\( x_0 = 0.01 \)として計算してみると、
最後に、初期値\( x_0 = 0.01 \)として計算してみると、
表1.3-3 \( x_0 = 0.01 \)での\( f(x)=0 \)の解
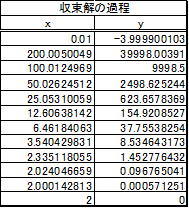 この場合、反復計算は12回必要になりました。
通常、初期値を変えれば反復計算の回数も変わります。
この場合、反復計算は12回必要になりました。
通常、初期値を変えれば反復計算の回数も変わります。
1.3.ニュートン法の証明
<命題>
区間[a,b]において、\(f(x)\)は二階以上微分可能とします。 このとき、\( f''(x) > 0 、f(a) < 0, f(b) > 0 \)ならば\( x^{(0)} = b \)とおいて、数列\[
x^{(i+1)} = x^{(i)} - \frac{ f(x^{(i)}) }{ f'(x^{(i)}) }
\]
は\( f(x) = 0 \)のただ一つの解\( x_t \)に収束します。
証明 ******************************
\( f''(x) > 0 \)なので、\( f'(x) \)は単調増加、は下に凸の関数になります。
また、\( f(a) < 0, f(b) > 0 \)の条件とあわせれば、\( f(x) = 0 \)の解\( x_t \)は[a,b]にただ一つ存在します。
ここで[\(x_t \),b]に着目します。 \( f'(c) = 0 \)を満たすcがこの区間内に存在すると仮定すると、\( f(c) \)は関数\( f(x) \)の最小値をとります。 従って、\( f(x_t) = 0 > f(c) \)となります。 \( f(b) > 0 \)から[c,b]の範囲で\( f(x) = 0 \)は解を持つことになりますが、これは前述のただ一つの解の存在と矛盾します。
次に、[\(x_t \),b]で\( f'(x) < 0 \)とすれば、\( f(x) \)は単調減少となり、\( f(x_t) = 0 \), \( f'(x) > 0 \)と矛盾します。
以上から、[\(x_t\),b]で\( f'(x) > 0 \), \( f(x) \)は単調増加となります。
このとき、数列\( x^{(n)} \)は\( f(x^{(n)})/f'(x^{(n)}) > 0 \)であるから単調減少となります。
さらに、の極限を\( \alpha \)とすると、

ここで[\(x_t \),b]に着目します。 \( f'(c) = 0 \)を満たすcがこの区間内に存在すると仮定すると、\( f(c) \)は関数\( f(x) \)の最小値をとります。 従って、\( f(x_t) = 0 > f(c) \)となります。 \( f(b) > 0 \)から[c,b]の範囲で\( f(x) = 0 \)は解を持つことになりますが、これは前述のただ一つの解の存在と矛盾します。
次に、[\(x_t \),b]で\( f'(x) < 0 \)とすれば、\( f(x) \)は単調減少となり、\( f(x_t) = 0 \), \( f'(x) > 0 \)と矛盾します。
以上から、[\(x_t\),b]で\( f'(x) > 0 \), \( f(x) \)は単調増加となります。
このとき、数列\( x^{(n)} \)は\( f(x^{(n)})/f'(x^{(n)}) > 0 \)であるから単調減少となります。
さらに、の極限を\( \alpha \)とすると、
\[
\alpha = \alpha - \frac{ f(\alpha) }{ f'(\alpha) }
\
\Leftrightarrow
\
f(\alpha)=0
\]
となって、\( \alpha \)は\( f(x) = 0 \)の解となります。
つまり、数列\( x^{(n)} \)は\( x_t \)に収束します。
****************************** おわり
1.4.ニュートン法の問題点
(1)関数\( f(x) \)の一階微分を自分で設定する必要があります。
\( f(x) \)が複雑な場合や、\( f(x) \)が自動的にモデル化されるような場合、対応は困難です。(2)解が収束するとは限りません。
例えば下図のような条件を満たしてしまうと、無限ループ化し、解は得られません。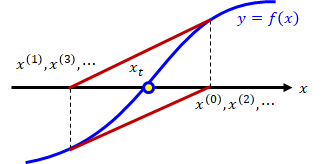 このような場合、初期解を少しずらすことで解決することがあります。
このような場合、初期解を少しずらすことで解決することがあります。
他に発散する場合もあります。 これは\( f'(x) = 0 \)となるxの値を初期値とした場合で、その接線はx軸と交わることはありません。 つまり初期値から計算が進展せず、\( f(x) = 0 \)の解を求めることはできません。
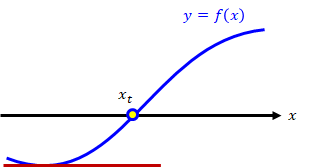
(3)初期解の決め方がはっきりしません。
真の解の近傍、と言われても、真の解は不明なため決めようがありません。 せいぜい関数をグラフ化してみて決めるぐらいしかありません。