Excel VBAを用いたニュートン法の使い方を説明します。
ニュートン法サンプル(NewtonMethod.zip)

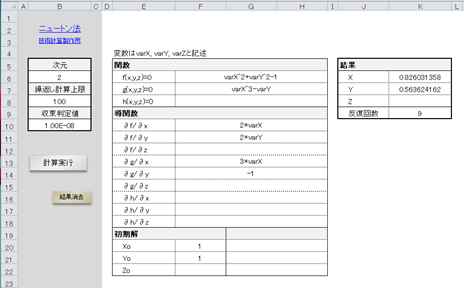
NewtonMethod.xlsmサンプル画面
ニュートン法の詳しい内容については、ニュートン法のページをご覧ください。1.入力
本ツールは、一変数~三変数までの関数に対応しています。関数は、Excel関数を入力するのと同じ方法で行います。 ただし、変数は次の通りとしてください。
- 一変数の場合:varX
- 二変数の場合:varX, varY
- 三変数の場合:varX, varY, varZ
(1)次元の設定
変数の数(次元)を設定します。 一変数関数の場合は“1”を、二変数関数の場合は“2”を、三変数関数の場合は“3”を選択します。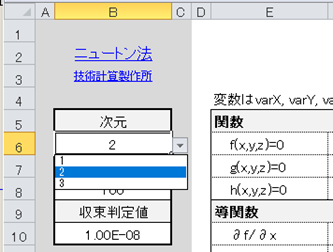
二変数関数の場合
(2)数式の入力
関数を文字列として入力します。 記述方法は“Excel関数”の記述方法と同じです。ただし、上述の通り変数はvarX、varY、varZで記述します。
なお、“=”は不要です。
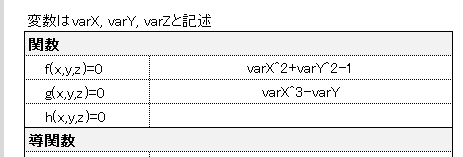
二変数関数の場合
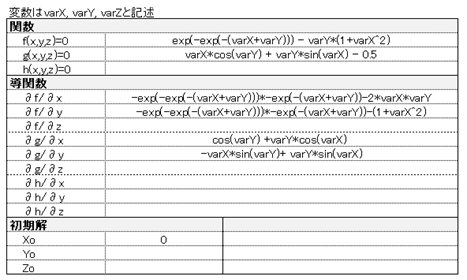
(3)偏微分関数の入力
各偏微分係数を自身で算出し、入力します。下図は二変数の場合で、この場合変数zは使っていませんのでその行は空白にしておきます (入力していても無視されます)。
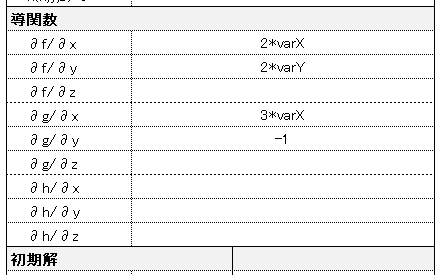
二変数関数の場合
なお、逆行列が存在しないケースは計算できません。(4)初期解の入力
初期解を入力します。空白時は“0”として扱われます。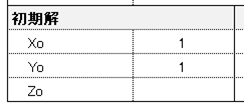
二変数関数の場合
(5)その他設定
ここは必要に応じて設定ください。 通常、特に設定を変更する必要はありません。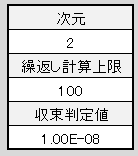
a)繰り返し計算上限
ニュートン法は反復計算によって解を得ます。 無限ループやいつまでも収束しないような場合に対応するため、繰り返し計算上限(回数)を設定します。b)収束判定値
ニュートン法によって得られる解は近似解です。 そのため、必要な精度を設定する必要があります。 収束判定値は小さいほど近似精度は向上しますが、繰り返し計算数は増加します。
2.出力
計算ボタンクリック後、結果が出力されます。 出力されるのは、近似解と繰り返し計算の回数(反復回数)です。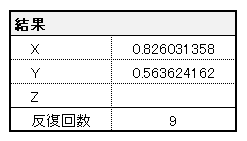 関数の入力ミスや、初期解が不適切な場合はエラーが発生する場合があります。
関数の入力ミスや、初期解が不適切な場合はエラーが発生する場合があります。
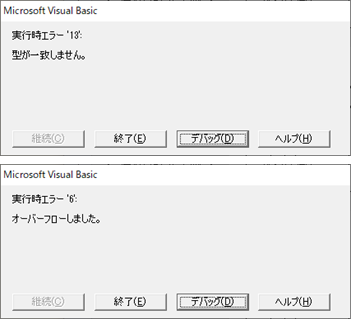
エラーの例
この場合は“終了”をクリックし、入力ミスのチェックや初期解の変更を行います。計算式が複雑になるとエラーチェックは大変ですが、頑張って探してください。
3.VBAの活用
NewtonMethod.xlsmはVBAを用いて計算を行っています。ソースはご自身のツール内に取り込んでいただいて構いません。 ただし、それによる損失等の補償は致しませんので、十分な検証を行ったうえでご活用ください。
二変数以上のニュートン法は行列演算が必要となります。 そのため、行列計算モジュール(M01_CalcMatrix)が組み込まれています。
VBA Moduleの構成
従って、M00_exeモジュールに記述されているNewton法ロジックをそのままコピー&ペースとしても使用できません。また、文字列入力した関数をVBA内で数式として扱えるようFunctionを定義しています (Function FuncEvaluate(x, y, z, ByVal funcF))。 ニュートン法のプログラムを組む際、Evaluate関数は使い勝手が良いため重宝します (Javascriptでも同じです)。


