1．公差

1．1．公差とは？

公差とは、「ある基準値に対するばらつきの許容範囲」のことです。
「公差を設定する」とは、例えば長さ50mmの棒を作るとき“±0.1mm”の範囲で長さが違ってもいいよ、とすることです。

図1.1-1　公差設定例

設計者はこの“公差”をどう決めるかで四苦八苦することになります。 その理由として次のようなものが挙げられます。

• 公差を緩く設定すると、組み立てられなくなったり、機能障害が出たりする
• 公差を厳しく設定すると、そのような範囲では作れないとか、作れたとしても非常に製造コストが高くつく

このように「公差を設定する」ことは製品の運命を決定付ける非常に重要な仕事であり、設計者の腕の見せ所になります。
特に公差設定において製造観点で意識しておくと良いのは、“作る”こと以上に検査するときの“測る”という行為にあります。 “測る”という行為は実は非常に難しく、その理由として

• 温度等の環境によって、材料が膨張・収縮し長さが変わってしまう
• 接触型の測定器（ノギスなど）で測ると、その押付力によって変形し、長さが変わってしまう
• 切断面は必ず凸凹したり傾いたりしているので、測定箇所によって長さが変わってしまう
• 測る場所によって重力加速度が変化し、重量が変わってしまう
• 測定器自体にいくらかの誤差を必ず含んでいる（分解能含め）

等があるためです。これらはすべて“誤差”という形で現れます。 上記理由により、仮に50mmピッタリの棒を作ったとしても、それを保証できるだけの測定を行うことは非常に難しく、公差設定では測定上の誤差（測定誤差といいます）を考慮する必要があります。

1．2．誤差について

ここでは“誤差”とはどういうものか？について見ていきます。
誤差とは、「本来の値（真値といいます）に対してどれだけずれているか？」を表すものです。 ただ残念なことに、我々が真値を知ることはほぼ不可能です。 通常、真値を知るためには測定を行わなければなりませんが、その測定自体に必ず誤差（測定誤差）が含まれるためです。 この測定誤差は次の二種類に大別できます。
このように製造上、少なくとも測定の段階で必ず誤差を含むことになるため、“公差0”の設定はできません。 つまり設計者は、公差設定において必ず誤差範囲を想定しなければなりません。その意味で

誤差範囲≦公差

の関係が成り立たなければなりません。 ところが、「誤差は確率と密接につながっている」ことが偶然誤差の話から分かるので、想定誤差範囲を有限な範囲とすることは理論上不可能です。 理由は、測定回数が∞のとき、ばらつきの分布は正規分布とるためです（発生確率が0になるためには 、 とならなければなりません。そのため、実質発生確率0は不可能ということになります）。

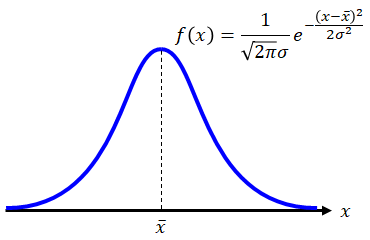
図1.2－1　正規分布

となると、公差を設定することも不可能なのでしょうか？
決してそんなことはなく、公差に確率的な意味を付加することで

「製品のばらつきが元となる不具合の発生確率をどれだけ抑制するか？」

という意味が公差設定の意義として与えられることになります。

1．3．公差の確率的解釈

公差の確率的な意味について考えてみます。
確率は「発生する事象がどのぐらいの割合で起きるか？」を表すものです。 図1.3－1の\(x\)軸と青線で囲まれた領域の面積が事象の発生確率になります。

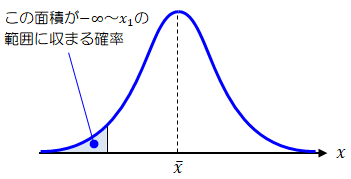
図1.3－1　発生確率

従って、-∞＜\(x\)＜+∞で\(f(x)\)を積分すればすべての事象を含むことになり、発生確率は1になります。 図1.3-1を見ると、\(x_{1}\)の値を小さくしていく、つまり\(x_{1}\)を左へ寄せていくと、\(x\)軸と青線の間の面積はものすごく小さくなることがわかります。 その結果、ある値より小さい範囲の発生確率はほとんど0に等しい、といえます（大きい側も同様に言えます）。 従って、“誤差の許容範囲=公差”を満たす発生確率が1に極めて近い値（例えば0.997）となるよう設定することで、誤差を逸脱する状況を極めて少なくすることができます（0.997なら1000個中3個が誤差を逸脱する可能性があります）。 このように、誤差が持つ確率的意味を理解した上で、公差を設定することが重要になります。

通常、公差設定で想定される確率分布は正規分布です。 それはどんな確率分布も、無数に試行すれば正規分布に漸近するためです。 また1に近い値として通常0.997（99.7%）が用いられます。これは標準偏差σの3倍となる範囲を意味しています。 例えば、ノミナル寸法をA、その公差を±aとするとき、正規分布をあてがうと下図のような関係になります。

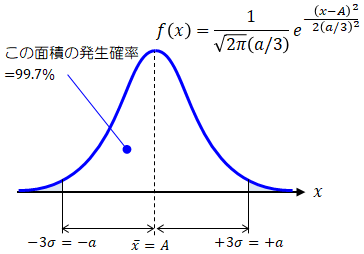
図1.3－2　公差と正規分布の関係

1．4．公差の設定方法

今までは製造観点を主に公差の設定について見てきました。 それ以外にも、機能・性能上の観点から公差の設定が必要となります。 どちらかといえば機能・性能の観点の方が重要です。 製造観点上どれだけ厳しい公差設定を設けたとしても、機能・性能要求を満たさなければ意味がありません。 従って、公差の設定は以下のフローをとるのが一般的です。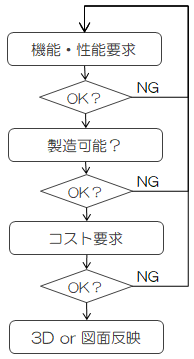

図1.4－1　公差の設定フロー

このように、機能・性能上の要求をまとめてから、それが製造可能か？の観点を加えて

機能・性能上の要求 ≧ コスト上の要求 ≧ 作れる or 作れないの要求

となるような公差範囲を模索していくことになります。 残念ながらこの不等式を一発で満たすことはなかなか難しく、不具合発生確率をどれだけ許容できるか？というところのバランスをみながら最終的に公差を設定していくことになります。

とはいえ、なかなかはじめからすべての公差設定根拠を数値的に示すことは非常に困難です。 従って誤差範囲の想定については、 経験則やJIS等の規格をもとに決めるのが一般的です。 また、ここでは正規分布を前提としてきましたが、経験上別の分布関数に従うと想定される場合は、 そちらの分布関数をもとに公差を設定しても構いません。
設計者には経験が求められるのは、このような理由があってのことです。
これは個人的な意見ですが、私自身は経験に縛られることなくまずは自由に設計してみて、その後実際の造りの現場の方たちと製法・検査方法含め議論し見直していくことが大事だと考えています。公差をどう決めていいかわからないからとりあえず経験者たちの話をうのみにして進めてしまうと、これまでと同じような技術しか生まれてきません。それでは設計者として面白くないでしょう？
自分なりの考えをしっかりもって設計していくことが設計者の仕事であって、それが製品の個性として現れるものだと考えています。

参考文献

関連ページ