情報エントロピー
1．情報の単位
私たちにとって最も簡単な情報は「二者択一」、つまり“はい”か“いいえ”で答えられる情報でしょう。例えば、
あの人は男ですか？
の問いに、“はい”と答えれば“男”という情報が得られ、“いいえ”と答えれば“女”という情報が得られます。 この二者択一の問いから得られる情報を“最小の情報量”=ビット（binary digit）と呼びます。二者択一の情報はコンピュータで扱えます。 その理由は次の通りです。
- コンピュータがON/OFFスイッチの集合体であること
- 「はい」=ON、「いいえ」=OFFとできること
従って、1ビットの情報とは「“1”または“0”のどちらかを選択すること」に他なりません。
2．情報量
2．1．情報量（ビット）
さきほどの「あなたは男ですか？」の問いからは、「あなたは男である」 「あなたは女である」
のどちらか1つの情報を得ることができるので、この質問は1ビットの情報量を持っています。この質問に「あなたは大人ですか？」を加えると、質問の答えは
（男∧大人） （男∧子供） （女∧大人） （女∧子供）
上の4通り（22=4）存在し、“男 or 女”、“大人 or 子供”の2つの情報が得られます。 このときの情報量は1ビットの質問を2つ組み合わせたものなので、2ビット（2の乗数に該当）になります。さらに「あなたは右利きですか？」の問いを加えれば、答えは次の8通り（=23）の中の1つになります。
（男∧大人∧右） （男∧大人∧左）
（男∧子供∧右） （男∧子供∧左）
（女∧大人∧右） （女∧大人∧左）
（女∧子供∧右） （女∧子供∧左）
この情報量は1ビットの質問を3つ組み合わせたものなので、3ビット（2の乗数に該当）になります。これを一般化すると、「答えの組み合わせが2n個ある質問の情報量」はnビットになります。
この定義によれば、答えが3つある質問の情報量は整数にはなりません （例えば「飲み物のサイズはどれにしますか？」の答えが“S”、“M”、“L”の場合）。
\[
2^n=3 \
\leftrightarrow \
n=log_{2}3
= \frac{\log_{\ 10}3}{\log_{\ 10}2}=\frac{0.477}{0.301}=1.585 (ビット)
\]
2．2．情報量と確率
前節で見たように、情報を得ることは「2n個ある答えの中から一つを選択すること」に他なりません。 このとき、一つの答えを選択する確率は1/2nとなります。ここで、この確率と情報量の間にある意味について考えてみます。
例えば一つの質問に対し、Aという答えが得られる確率を1/5、Bという答えが得られる確率を4/5とします。 このとき、Aという答えは5個の選択肢があってはじめて1個選択できることになるので、 情報量nAは次のようになります。
\[
2^{n_A} = \frac{1}{(\displaystyle\frac{1}{5})} = 5
\leftrightarrow
{n_A} = \log_{\ 2}5 = 2.322
\]
それに対しBという答えは、5個の選択肢がある中から4個選択、つまり1.25個の選択肢から1個選択することになります。
このときのBの情報量nBは次のようになります。\[
2^{n_B} = \frac{1}{(\displaystyle\frac{4}{5})} = 1.25
\leftrightarrow
{n_B} = \log_{\ 2}1.25 = 0.322
\]
結果、Aから得られる情報量とBから得られる情報量には差があり、
\[
{n_A} \gt {n_B}
\]
の関係が成り立ちます。
この結果から、「発生確率の低い事象（A）から得られる情報量は大きい」ということが言えます。
例えば「めったに見られない出来事からの情報が世間に与える衝撃は大きい」ことからも容易に想像がつくと思います。
以上の話から、確率Pの事象から得られる情報量n（ビット）は次式で求まります。
\[
n = \log_{\ 2}(\frac{1}{P})
\tag{2.2-1}
\]
3．情報エントロピー
エントロピーは、熱力学において“乱雑さ”を表す量として定義されたものです。例えば、2つの気体（AとB）が完全に交じり合った状態をイメージしてみます。
“エントロピーが大きい”状態は、2つの気体（AとB）が完全に交じり合った状態のことです。 それに対し“エントロピーが小さい”状態は、2つの気体が分離された状態のことです。 実際、交じり合った気体からAだけを取り出したり、Bだけを取り出すのは不可能です。
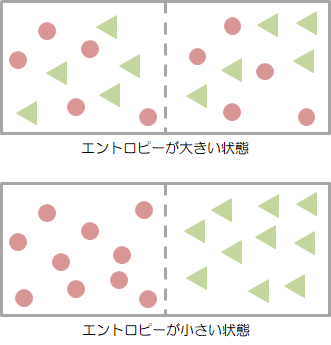このように、気体分子がぐちゃぐちゃに混ざった状態の度合い（乱雑度合い）を表したのが、エントロピーになります。
エントロピーをもう少し身近な例であてはめてみましょう。
部屋をきれいに片づけた状態がエントロピーの小さい状態、そこから日数が経って部屋中が無秩序に散らかりまくった状態がエントロピーの大きい状態、と考えてもらえばイメージしやすいかもしれません。
この「無秩序に散らばった状態」というものを情報の世界にも当てはめてみよう、というのが情報エントロピーです。 エントロピーの意味から考えて、きちんと整理整頓された情報は情報エントロピーが小さく、逆にいろんな情報がとっちらかって存在し、それらをまとめても何ら情報として価値を持たない場合、情報エントロピーは大きいとします。
この情報エントロピーを定量化するために、次のように定義します。
ある事象が起こる確率をPi、そこから得られる情報量をniとするとき、エントロピーHを次式で定義します。
\[
H = \sum_{k=1}^{n} P_{i}n_{i}
= \sum_{k=1}^{n} P_{i}\log_{\ 2}\frac{1}{P_{i}}
= -\sum_{k=1}^{n} P_{i}\log_{\ 2}P_{i}
\tag{3-1}
\]
「ある質問や行為（＝情報源）から平均的に得られる情報量の予測値」
このエントロピーHがどのようなグラフ特性を示すか？について見てみます。ある事象Aが発生する確率をP、Bが発生する確率を1－Pとしたとき、エントロピーの特性は次のようになります。
\[
H = -P \log_{\ 2}P - ( 1 - P ) \log_{\ 2}(1-P)
\]
Pは確率であるため0≦P≦1であり、これを考慮に入れてグラフを描くと下図のようになります。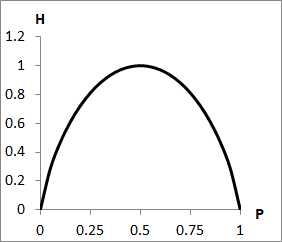
このようにエントロピーHは確率Pに対して上に凸な関数となります。またエントロピーHを最大にする確率Pは\[
\frac{dH}{dP} = \log_{\ 2}(1-P)-\log_{\ 2}P=0
\leftrightarrow
P=\frac{1}{2}
\]
1/2になります。つまり、発生確率の等しいな情報=五分五分の予想から得られる情報のエントロピーが最大となり、発生確率の差が大きな情報のエントロピーは小さくなります （五分五分の予想をもとに何かを決めるのは、“丁”か“半”かのばくち打ちとほとんど変わらないことを意味しています）。
ここで相撲を例にとり、情報のエントロピーを実際に計算してみます。
横綱Aさんと平幕Bさんの対戦から得られるエントロピー、平幕Bさんと平幕Cさんの対戦から得られるエントロピーを計算します。 横綱Aさんと平幕Bさんの対戦成績は20勝5敗とし、この力関係は普遍的と見ます。 すると横綱Aさんが平幕Bさんに勝つ確率と、平幕Bさんが横綱Aさんに勝つ確率は次のようになります。
横綱Aさんが平幕Bさんに勝つ確率：\( \frac{4}{5} = P_{1} \)
平幕Bさんが横綱Aさんに勝つ確率:\( \frac{1}{5} = P_{2} \)
このとき、確率P1、P2から得られる情報量をそれぞれn1、n2とすると次のようになります。
\[ n_{1} = \log_{\ 2}(1.25) = 0.322 \]
\[ n_{2} = \log_{\ 2}5 = 2.322 \]
これを（3－1）式に代入すると、この対戦から得られる情報エントロピーは次のようになります。\[
H_{AB} = \sum_{k=1}^{2}P_{i}n_{i}
= \frac{4}{5} \times 0.322 + \frac{1}{5} \times 2.322
= 0.722
\]
それに対し、平幕Bさんと平幕Cさんの対戦成績は10勝10敗の五分だとすると、この情報エントロピーは次のようになります。\[
H_{BC}
=
\frac{1}{2} \log_{\ 2}\frac{1}{\frac{1}{2}} + \frac{1}{2} \log_{\ 2}\frac{1}{\frac{1}{2}}
=
1
\]
横綱Aさんと平幕Bさんの情報エントロピーと、平幕Bさんと平幕Cさんの情報エントロピーをグラフ上に記すと、
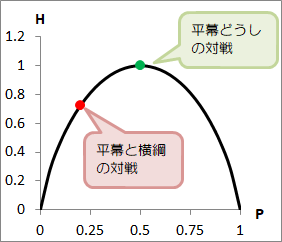図で示したように、横綱Aさんと平幕Bさんの対戦に対するエントロピーは極大点から外れており、横綱の方が勝つ確率が高い、という価値を情報は持ちます。
それに対し、平幕Bさんと平幕Cさんの対戦に対するエントロピーは極大点にあり、確率的にもどっちが勝つか予想がつきませんので、情報としてはあまり価値がないものになります。
