圧入計算式
ここではWebAPPで使用している圧入計算式について紹介します。1．はめあい代
圧入計算は、2つの厚肉円筒の組み合わせとして考えます。各パラメータの添字について軸側を“s”、穴側を“h”とし、添字のないものは共通パラメータとします。 圧入における主設計パラメータは、“軸の外径”と“穴の内径”です。 そこで呼び径\( D \)を共通とし、それぞれの公差を次のように設定します。
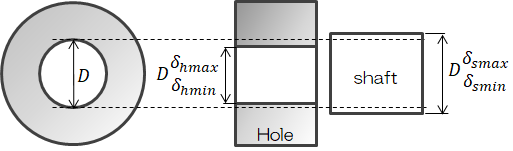次に、温度条件によってはめあい代は変化するので、それを考慮します。圧入時と径測定時の温度をそれぞれ\( T_i,T_{io} (i = s, h) \)、線膨張係数を\( \alpha_i \)とすると、圧入時の径は次式で表せます。
\[
D'_i
=
{ 1 + ( T_i - T_{io} ) \alpha_i } D_i
\tag{1}
\]
なお、通常径測定時の温度\( T_{io} \)は常温（20℃）程度です。
温度を考慮した見かけの締め代を次のように設定します。
\[
\delta_{max}
=
D'_{smax} - D'_{hmin}
\\
\delta_{min}
=
D'_{smin} - D'_{hmax}
\tag{2}
\]
このとき、\( \delta \leq 0 \)なら計算はここで終了になります（すきまばめのため）。
2．つりあい条件
さて、圧入は軸外径と穴内径が一致し、その接触部に発生する圧力が互いにつりあう状態にあります。 このときの軸外径 = 穴内径を\( D_c \)、つりあい圧力を\( p_c \)とします。そうすると、軸外径の変形量\( u_s \)と穴内径の変形量\( u_h \)は、厚肉円筒の応力式（\( \sigma_z = 0 \)）
\[
u
=
\frac{ ( 1 + \nu ) ( p_1 - p_2 ) r_1 ^2 r_2 ^2}{ E ( r_2 ^2 - r_1 ^2 ) r }
\quad
+
\frac{ ( 1 - \nu ) ( p_1 r_1 ^2 - p_2 r_2 ^2 ) r }{ E ( r_2 ^2 - r_1 ^2 ) }
\]
を用いて、軸は\( r_{s2}=r_c, p_1=0, p_2=p_c \)、穴は\( r_{h1}=r_c 、p_1=p_c 、p_2=0 \)として次のように表せます。
\[
u_s
=
-p_c r_c \biggl\{
\frac{ ( r_c^2 + r_{s1}^2 ) }{ E_s ( r_c^2 - r_{s1}^2 ) }
- \frac{ \nu_s } { E_s } \biggr\}
\tag{3}
\]
\[
u_h
=
p_c r_c \biggl\{
\frac{ ( r_{h2}^2 + r_c^2 ) }{ E_s ( r_{h2}^2 - r_c^2 ) }
+ \frac{ \nu_h } { E_h } \biggr\}
\tag{4}
\]
軸の変形量\( u_s \)は収縮側なので“-”、穴の変形量\( u_h \)は膨張側なので“+”になります。
ただし、これらの式の中には4つの未知数\( p_c, r_c, u_s, u_h \)が含まれます。
また、幾何学的な条件から\( r_c, u_s, u_h \)は次の関係を持ちます。
\[
u_s
=
r_c - r_{s2}
\tag{5}
\]
\[
u_h
=
r_c - r_{h1}
\tag{6}
\]
そこで、\( r_c \)を変化させながら軸と穴の\( p_c \)がおおむね一致するまで収束計算を行うことで、これら4つの未知数を近似的に決定します。
このとき、\( r_c \)の初期値は以下のように決める。
\(
r_c^{(0)}
=
\frac { D'_{smax} + D'_{hmin} } { 2 }
\)
(締め代最大時）
\(
r_c^{(0)}
=
\frac { D'_{smin} + D'_{hmax} } { 2 }
\)
(締め代最小時）
（3）～（6）式に代入し、を計算する。軸と穴の\( p_c \)の絶対値の差が微小値（例えば10-6）以下になれば、一致したものと判定します。
そうならなければ\( r_c \)を変えて再計算します（本サイトでは二分法を用います）。
収束完了がしたとき、4つの未知数\( p_c, r_c, u_s, u_h \)は確定し、この確定値をもとに周方向応力\( \sigma_t \)が定まります。 これもまた厚肉円筒の発生応力式をもとに求められる（径方向応力は\( p_c \)である）。
\[
\sigma_t
=
\frac{ p_1 r_1 ( r_2 ^2 + r^2 ) - p_2 r_2 ( r^2 + r_1 ^2 ) }
{ r^2 ( r_2 ^2 - r_1 ^2 ) }
\]
このとき、軸は\( r_{s2}=r_c,p_1=0、p_2=p_c\)、穴は\( r_{h1}=r_c 、p_1=p_c 、p_2=0 \)として代入します。
\[
\sigma _{st}
=
\frac{ -p_c ( r_c ^2 + r_{s1} ^2 ) }{ ( r_c ^2 - r_{s1} ^2 ) }
\tag{7-1}
\]
\[
\sigma _{ht}
=
\frac{ p_c ( r_{h2} ^2 + r_c ^2 ) }{ ( r_{h2} ^2 - r_c ^2 ) }
\tag{7-2}
\]
3．圧入荷重・スリップトルク
さらに、圧入荷重とスリップトルクは次のようにして求められます。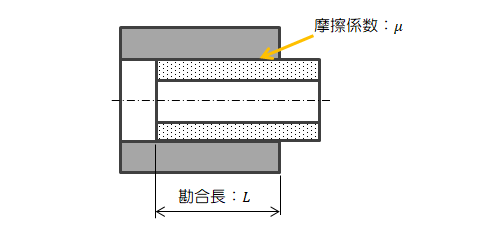
接触面に発生する\( p_c \)を接触全域で積算することで、垂直抗力\( N \)として作用します。
\[
N
=
p_c \cdot 2 \pi r_c L
\tag{8}
\]
従って圧入荷重\( F_p \)は、接触面の摩擦力\( \mu N \)より大きくなければなりません。
\[
F_p
\geq
\mu N
=
2 \pi \mu r_c L p_c
\tag{9}
\]
またスリップは、接触面の摩擦力（結局\( F_p \)と同じ）によって生じるトルクより大きなトルクが加わると発生します。
従って、スリップトルク\( T_s \)は次のようにして求められます。
\[
T_s
\geq
\mu N r_c
=
F_p r_c
\tag{10}
\]
4．さいごに
このページは「圧入計算をどのように行っているか？」について説明しただけです。 理論的な成り立ちについては触れていません。 圧入で発生する応力は、厚肉円筒の式を用いて計算しています。 この導出は“材料力学”ページに記していますので、そちらもあわせて参照ください。 またさらに、厚肉円筒の式は弾性理論から導かれるもので、より深く材料力学の原理を知りたい場合は“弾性理論”ページを参照ください。
