連続体力学
2.連続体の変形
2.1.変位ベクトル
物体内の任意の点Pの移動に着目します。ただし、Pは拘束点ではないものとします。点Pの位置ベクトルを\( \bf{r} \)、移動後の点P'の位置ベクトルを\( \bf{r'} \)とするとき、Pを始点、P'を終点とするベクトル\( \bf{u} \)を変位ベクトルと呼びます。 \( \bf{u} \)は点PからP'への移動を表していますので、位置が変わる=変位を意味することがわかります。
\[
\bf{u}=\bf{r'} - \bf{r}
\tag{2.1-1}
\]
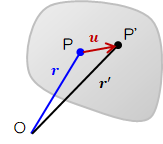
図2.1-1 変位ベクトル
また、変位ベクトル\( \bf{u} \)は元の位置ベクトル\( \bf{r} \)によって定まるため、\( \bf{r} \)の関数\( \bf{u} = \bf{u} (\bf{r}) \)になります (以降の話はこれを前提にしていますので重要です)。2.2.変形
2.2.1.変形の定義
物体の形や容積が変わることを変形といいます。 変形の際、物体内の各点は、変位に伴って各点間距離も必ず変化します。 もし、物体内の各点が変位しているにもかかわらずその距離が変化しない場合、物体は変形せず並進や回転運動をしていることになります (図右側)。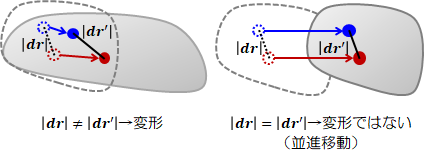
図2.2.1-1 物体の変形
2.2.2.変形テンソル
物体内の近接する任意の二点P、Qに着目します。 それぞれの位置ベクトルを\( \bf{r} \)、\( \bf{r} \)+d\( \bf{r} \)とします (近接点なのでd\( \bf{r} \)は微小ベクトル)。物体が変形して点P→P'、点Q→Q'に変位したとき、P、Qそれぞれの変位ベクトルは\( \bf{u}( \bf{r} )、\bf{u}( \bf{r} + d \bf{r} ) \)で表せます。
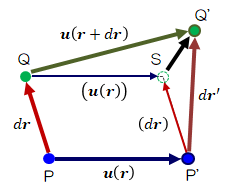
図2.2.2-1 物体の変形に伴う変位
このとき、次の関係式が成り立ちます。\[
\overrightarrow{ SQ' }
=
d \bf{r'} - d \bf{r}
= \bf{u} ( \bf{r} + d \bf{r} ) - \bf{u} ( \bf{r} )
\tag{2.2.2-1}
\]
\( d \bf{r} \)は微小ゆえテイラー展開して二次以上の微小項を無視し、次のように近似します。
\[
d \bf{r'} = d \bf{r} + \frac {\partial \bf{u} ( \bf{r} )}{\partial \bf{r}} d \bf{r}
\tag{2.2.2-2}
\]
これは、変形によって生じる近傍点の変位差を表します。
特に右辺第二項を成分表示すると次のようになります。
\[
\begin{eqnarray}
\frac {\partial \bf{u} ( \bf{r} )}{\partial \bf{r}} d \bf{r}
&=&
\left(
\begin{array}{c}
\displaystyle \frac {\partial u_x}{\partial x} dx +
\frac {\partial u_x}{\partial y} dy +
\frac {\partial u_x}{\partial z} dz \hspace{10px}
\\
\displaystyle \frac {\partial u_x}{\partial x} dx +
\frac {\partial u_x}{\partial y} dy +
\frac {\partial u_x}{\partial z} dz \hspace{10px}
\\
\displaystyle \frac {\partial u_x}{\partial x} dx +
\frac {\partial u_x}{\partial y} dy +
\frac {\partial u_x}{\partial z} dz \hspace{10px}
\end{array}
\right) \\
&=&
\left(
\begin{array}{ccc}
\displaystyle \frac {\partial u_x}{\partial x} &
\displaystyle \frac {\partial u_x}{\partial y} &
\displaystyle \frac {\partial u_x}{\partial z}
\\
\displaystyle \frac {\partial u_y}{\partial x} &
\displaystyle \frac {\partial u_y}{\partial y} &
\displaystyle \frac {\partial u_y}{\partial z}
\\
\displaystyle \frac {\partial u_z}{\partial x} &
\displaystyle \frac {\partial u_z}{\partial y} &
\displaystyle \frac {\partial u_z}{\partial z}
\end{array}
\right)
\left(
\begin{array}{c}
dx \\
dy \\
dz
\end{array}
\right) \\
\end{eqnarray}
\tag{2.2.2-4}
\]
\( d \bf{r} \)の係数行列の各成分は、変位ベクトル成分の各軸方向の変化量を示しています。
また、この係数行列はベクトル解析で知られているとおり、ベクトル\( \bf{u} (\bf{r}) \)の勾配\( \nabla \bf{u} \)で表せます。
\[
\left(
\begin{array}{ccc}
\displaystyle \frac {\partial u_x}{\partial x} &
\displaystyle \frac {\partial u_x}{\partial y} &
\displaystyle \frac {\partial u_x}{\partial z}
\\
\displaystyle \frac {\partial u_y}{\partial x} &
\displaystyle \frac {\partial u_y}{\partial y} &
\displaystyle \frac {\partial u_y}{\partial z}
\\
\displaystyle \frac {\partial u_z}{\partial x} &
\displaystyle \frac {\partial u_z}{\partial y} &
\displaystyle \frac {\partial u_z}{\partial z}
\end{array}
\right)
=
\left(
\begin{array}{c}
\displaystyle \frac {\partial }{\partial x} \\
\displaystyle \frac {\partial }{\partial y} \\
\displaystyle \frac {\partial }{\partial z}
\end{array}
\right)
\left(
\begin{array}{c}
u_x & u_y & u_z
\end{array}
\right)
=
\nabla \bf{u}
\tag{2.2.2-5}
\]
テンソルの定義により、ベクトルの勾配は二階のテンソルであることから、係数行列(2.2.2-5)を変形テンソルと呼びます。


