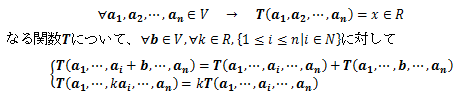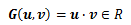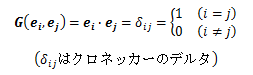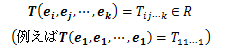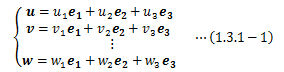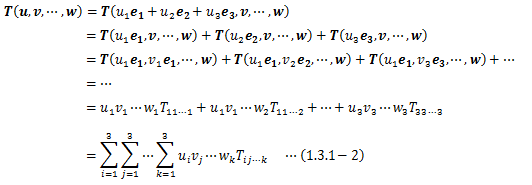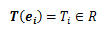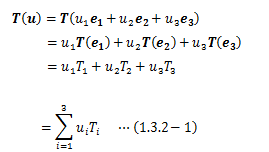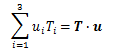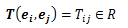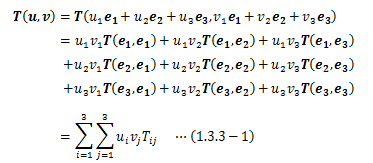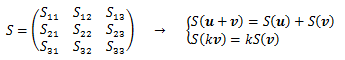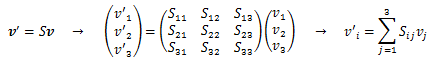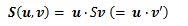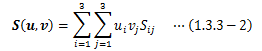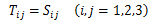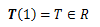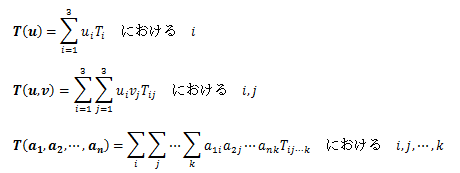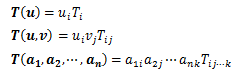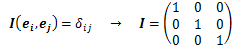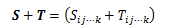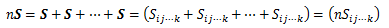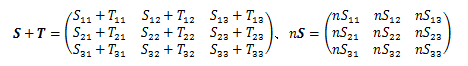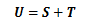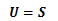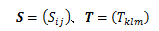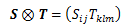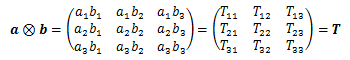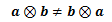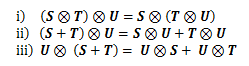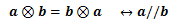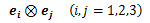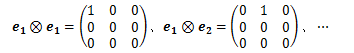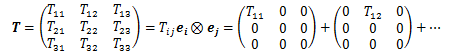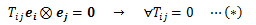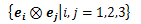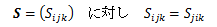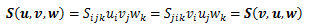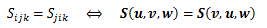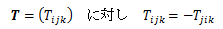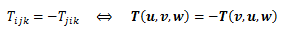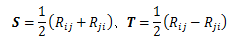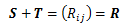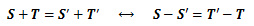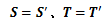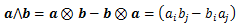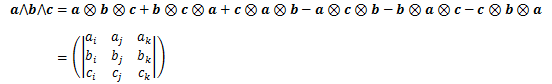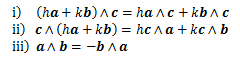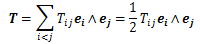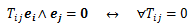1．テンソル

本章以降しばらくはテンソルの理解を得るために、特に指定がない限り、 自然数全体の集合をN、実数全体の集合をR、三次元ベクトル空間をVとして話を進めます。 また、ベクトル空間の正規直交基底を ｛e₁, e₂, e₃｝で表します。

1．１．テンソルの定義

n個のベクトルa₁、a₂、・・・、a_n を実数xに写す多重線形性を持つ関数Tをテンソルといい、 この定義を記号表記すると次のようになります。

特にベクトルの個数をテンソルの階数とよび、 上述のテンソルはn階のテンソルといいます。

1．2．基本計量テンソル

ベクトル空間において、ベクトルの内積演算が定義された空間を計量ベクトル空間と呼びます。 ベクトルの内積を定義することで、大きさや向きといった幾何学的意味が ベクトルに付与されることから、計量という言葉がうまくマッチしていると思います。
さて、前節でテンソルはベクトルを実数に写す線形写像である、と定義されました。 この定義にベクトルの内積は当てはまります。 そこで、空間内の任意のベクトルu、vの内積を関数Gと取れば、

であり、Gはu、vに対して双線形性（n＝2の多重線形性） を有することから二階テンソルと考えることができます。 この内積によって定義された二階テンソルGを 基本（計量）テンソルといいます。 テンソルGは2つの正規直交基底ベクトル e_i、e_j（i,j＝1,2,3）に対し以下を満足します。

1．3．テンソルの成分

1．3．1．直交性テンソル

n個の正規直交基底ベクトルe_i, e_j, …,e_k （i,j,…,k＝1,2,3）に対するテンソルの像を

で表します。このときテンソルの像である実数は3ⁿ個得られます。
次に、n個の任意ベクトルu、v、…、wは 正規直交基底の一次結合として次のように表せます。

このn個の任意ベクトルに関するテンソルの像を、テンソルの多重線形性を用いて計算すると、

が得られます。このとき3n個のT_ij…kの値を知ればテンソルの像である実数 T（u,v,…,w）が決まるため、Tij…kはテンソルの成分となります。 また、この添字の数はベクトルの数nと一致するので、n階テンソル成分の添時の数はnになります。 以上のように、正規直交基底に対して定義されたテンソルを 直交性テンソルと呼びます。

1．3．2．一階テンソルの成分

1.3.1節の定義をもとに一階テンソルの成分を定めます。
1個の正規直交基底ベクトルeiに対する一階テンソルの像を

で表せば、その像である実数は3個得られます。 ここで、任意ベクトルuに関する一階テンソルの像を、テンソルの線形性を用いて計算すると、

が得られます。 この式は、T_iを成分とするベクトルTと任意ベクトルuの内積の形をとっており、 また内積演算は任意ベクトルuに対して線形性を満足します。

以上から、一階テンソルTは内積演算を伴うベクトルの形態をとることがわかります。 つまり、一階テンソルはベクトルと同等と言えます。

1．3．3．二階テンソルの成分

1.3.1節の定義をもとに今度は二階テンソルの成分を定めます。
2個の正規直交基底ベクトルe_i、e_jに対する二階テンソルの像を

とおくと、その像である実数は9個得られます（T_ij≠T_ji）。 ここで、任意ベクトルu、vに関する二階テンソルの像を、 その双線形性を用いて計算すると、

が得られます。二階テンソルの成分はこの9個の実数T_ijとなります。
ここで、ベクトルの線形変換に着目します。 線形変換をSとしたとき、Sは三次正方行列（三次元のため）をとり、この変換は線形性を満足します。

この線形変換Sをベクトルvに作用させて得られたベクトルv'と、

任意のベクトルuとの内積は実数をとることから、関数Sを

と定義します。 線形変換も内積も、ともにu、vに対して線形性を有することから 関数Sは二階テンソルになります。 さらに上式を成分計算すると、

が得られ、（1.3.3－1）式と（1.3.3－2）式は全く同型をとることから、 二階（直交）テンソルの成分は、線形変換行列Sの成分と一致します。

以上から、二階テンソルTは行列演算と内積演算を伴う正方行列 の形態をとることがわかります。 つまり、二階テンソルはベクトルの線形変換と同等と見ることができます。
なお、n≧3の高階テンソルについてはすでに1.3.1節でその成分を見ましたが、 その形態はすでにベクトルや行列といったものを超越したマトリックス構造を持つため、 何とも表現できません。

1．3．4．0階テンソル

スカラーは一次元ベクトルとして扱えます。 一次元ベクトルの基底は1であり、これに関するテンソルの像はただ一つ得られます。

さらにこれまで同様、スカラーと同等である任意一次元ベクトルuに関するテンソルの像を計算すると、

であり、これは、ただ単にスカラーをスカラーに写しているだけに過ぎません。 このスカラーに関するテンソルの成分は、添字の数が0であるため0階テンソル （1.3.1節参照）といい、 その形態はスカラーをとります。

1．4．アインシュタインの規約

テンソルの成分表記では、Σ記号を多数含みます。この記号を毎回書くのは骨が折れる作業です。 そこで注目すべきは、テンソルの成分表記において、総和をとっている指標i,j,・・・,kが1つの項に2度繰り返し現れているものがあります。

そこで、1つの項に2度繰り返して現れる指標については、その指標の範囲について総和をとるものとします。 これをアインシュタインの規約と言います。 上記例をこの規約に基づき書き直すと、次のようになります。

また、総和をとっている指標を他の指標に置き換えても、結果に対し影響を与えません。

1．5．テンソル代数

1．5．1．単位テンソル・零テンソル

線形変換の中で恒等変換Iを有する二階のテンソルの成分は、

であり、単位行列と一致します。このテンソルIを単位テンソルといいます。
次に、任意のn個のベクトルに対するn階のテンソルが常に0をとるものを、 零テンソルと呼び、一般にOで表します。

1．5．2．テンソルの和

同じ階数の2つのテンソルS、Tについて、 同一添字同士の成分を足し合わせたものをテンソルの和といいます。

今度は、同じテンソルSをn個足し合わせると、

Sの成分はすべてn倍されます。これをテンソルのスカラー倍といいます。 例えば、二階のテンソルにおける和とスカラー倍は次のようになります。

次にテンソルUを

で定義するとき、テンソルTが零テンソルならば、

が成り立ちます。このときテンソルUとSは、対応するすべての成分が等しくなり、 このときテンソルUとSは等しい、と言います。

1．5．3．テンソル積

階数が異なっても良い2つのテンソル

に対して、すべての成分の相互積を成分にもつテンソルをテンソル積と言い、 次のように表します。

このテンソル積の階数は、Sの階数sとTの階数tの和s＋tになります。 なおテンソル積の演算自体は、テンソルでない成分に対しても行えるもので、 そういった意味で、テンソルの定義とテンソル積の演算の定義は切り離して捉えておく必要があります。
例えば、2つの一階テンソルのテンソル積は

となり、9個の成分を持つ二階テンソルになります。 また、一般にテンソル積に交換則は成り立ちません。

テンソル積の演算に関しては、次の定理が成り立ちます。

＜定理1＞

＜定理2＞

次に、正規直交基底のテンソル積について考えます。 まずは、二階テンソルのテンソル積

については、唯一の成分（i,j）のみが1で、それ以外の成分はすべて0になります。

このテンソル積9個はすべて互いに異なります。 これは正規直交基底が互いに独立であることの結果です（定理2 によります）。 このとき、次の定理が成り立ちます。

＜定理3＞

1．6．対称・交代テンソル

1．6．1．対称・交代テンソル

二階以上のテンソルについて、

という性質を持つとき、テンソルSは指標i、jについて対称といいます。 このとき、任意のベクトルu、v、wに対して

となり、i、jに関して対称とは、u、vに対して交換が成り立つことと同値になります。

次に、

という性質を持つとき、テンソルTは指標i、jについて交代といいます。 交代テンソルについても、対称テンソル同様に

が成り立ちます。

1．6．2．二階テンソルの分解

二階の対称・交代テンソルについて見ていきます。

＜定理1＞

＜定理2＞

特に定理2については次のようにして証明されます。 任意の二階テンソルRに対して

とおくと、

となります。また、他の対称・交代テンソルS'、T' によって任意のテンソルRが表せたとすると、

これは定理1により零テンソルになるため、

となり、任意の二階テンソルRに対し、対称テンソルS、 交代テンソルTは一意に定まります。

1．6．3．交代積

ベクトルa、bに対して

で定義される二階テンソルをaとbの交代積といいます。
3つのベクトルにたいして交代積を拡張すると、以下のようになります。

ここで、交代積は次のような定理を持ちます。

＜定理1＞

＜定理2＞

参考文献

関連ページ