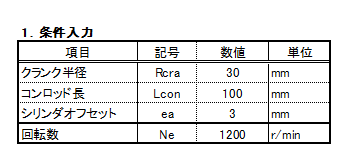
機構学
2.クランク機構
クランク機構は“回転運動を直線運動に変換する”機構です。 機構の代表的な例として、車のエンジンが挙げられます。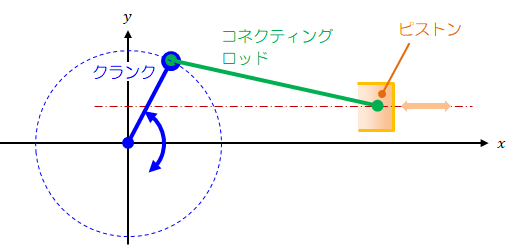
図1-1 クランク機構
クランク機構では、回転力が発生しない箇所が存在し、その箇所を死点(DC:Dead Center)と呼びます。 特に、ピストンの最も高い位置にある死点を上死点(TDC:Top Dead Center)、低い位置の死点を下死点(BDC:Bottmo Dead Center)と呼びます。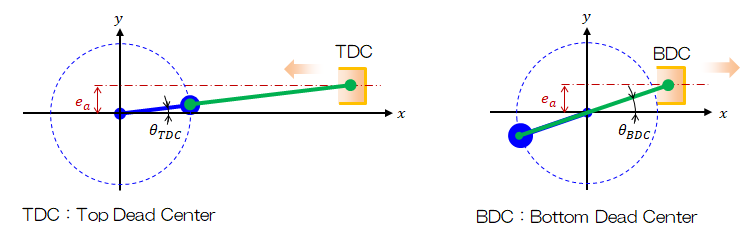
図1-2 クランク機構の死点
2.1.クランク機構の計算
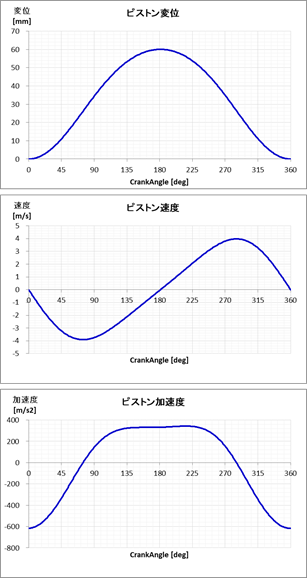
クランク機構ではピストンの変位、速度、加速度が重要になりますので、これらの計算方法について説明していきます。そこでまずは、クランク機構のパラメータを下図のように設定します。
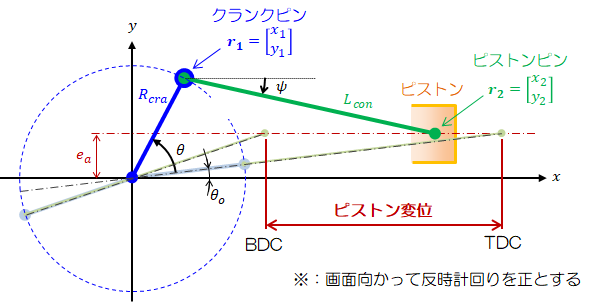
図2-1 クランク機構計算に用いる変数
| 変数名 | 記号 |
|---|---|
| ・クランク半径 | \( R_{cra} \) |
| ・コネクティングロッド長 | \( L_{con} \) |
|
・シリンダオフセット (シリンダ中心軸のずれ量) |
\( ea \) |
| ・クランク回転角 (TDCのとき0) |
\( \theta \) |
次に、クランク機構を計算する上での前提条件を次のようにとります。
- 二次元平面内の運動とする。
- 回転角\( \theta = 0 \)を、クランク回転中心と上死点(TDC)を結ぶ線上にとる。
- 幾何学的拘束条件:
\[ ( R_{cra} + L_{con} \ ) \sin \theta_o = ea \tag{2-1} \] - 位置ベクトル初期値:
\[ \bf{r_{cra}} = \left( \begin{array}{c} R_{cra} \\ 0 \end{array} \right) , \ \bf{L_{con}} = \left( \begin{array}{c} L_{con} \\ 0 \end{array} \right) \tag{2-2} \] - z軸周りの回転行列(z軸は画面手前方向):
\[ R(\theta) = \left( \begin{array}{c c} \cos \theta & - \sin \theta & \\ \sin \theta & \cos \theta & \end{array} \right) \tag{2-3} \]
- 回転行列\( R(\theta) \)の時間微分(二次元平面内の運動に限る):)
\[ \begin{eqnarray} & \frac{dR( \theta )}{dt} & = \dot{\theta} \\ \\ & \frac{d^2 R( \theta )}{dt^2} & = \ddot{\theta} R(\theta+\frac{\pi}{2}) -\dot{\theta}^2R(\theta) R(\theta+\frac{\pi}{2}) \end{eqnarray} \tag{2-4} \]なお、クランク回転が等速円運動のとき、\( \dot{\theta} = const \)なので、
\[ \frac{d^2 R( \theta )}{dt^2} = -\dot{\theta}^2R(\theta) \tag{2-5} \]
(1)ピストンの運動範囲
幾何学的条件から、ピストンストローク、TDC、BDCの角度は次のようにして求まります。a)ピストンストローク
\[
St
=
\sqrt{ ea^2 + (L_{con} + R_{cra})^2}
\ -
\sqrt{ ea^2 + (L_{con} - R_{cra})^2}
\tag{2-6}
\]
b)TDC、BDCの角度
\[
\begin{eqnarray}
& \theta_{TDC} &
=
\sin^{-1} \displaystyle \frac{ea}{L_{con} + R_{cra}}
\\
\\
& \theta_{BDC} &
=
\sin^{-1} \displaystyle \frac{ea}{L_{con} - R_{cra}}
\end{eqnarray}
\tag{2-7}
\]

図1-2 クランク機構の死点
(2)ピストン変位
ここでもう一度、図2-1に登場してもらいます。
図2-1 クランク機構計算に用いる変数
コネクティングロッドとクランクの成す角\( \psi \)は上図からわかるように、\( \theta \)の関数になります(以降、\( \theta' = \theta + \theta_o \)とします)。
\[
L_{con} \ \sin \psi
=
R_{cra} \sin( \theta ' ) - ea
\tag{2-8}
\]
\[
\Leftrightarrow \
\psi ( \theta ' ) = \sin^{-1} \frac{R_{cra} \sin ( \theta ' ) -ea}{L_{con}}
\tag{2-9}
\]
クランクピンの位置ベクトル\( \bf{r_1} \)はクランクの初期ベクトル\( \bf{r_{cra}} \)を回転角\(\theta\)で回すことで決まります。 また、ピストンピンの位置ベクトル\( \bf{r_2} \)は、コネクティングロッドの初期ベクトル\( \bf{L_{con}} \)をクランクピン周りに回転角\(\psi\)で回したものを、クランクピンの位置ベクトル\( \bf{r_1} \)に足し合わせるだけです。 これらの計算は回転行列(2-4)式を用いることで簡単に求めることができます。
\[
\begin{eqnarray}
& \bf{r_1} &
=
R( \theta' ) \bf{r_{cra}}
=
\left(
\begin{array}{c}
R_{cra} \cos (\theta') &
\\
R_{cra} \sin (\theta') &
\end{array}
\right)
\\
\\
& \bf{r_2} &
=
\bf{r_1} +
R( -\psi ) \bf{r_{con}}
=
\left(
\begin{array}{c}
R_{cra} \cos (\theta') + L_{con} \cos \psi &
\\
R_{cra} \sin (\theta') - L_{con} \sin \psi &
\end{array}
\right)
=
\left(
\begin{array}{c}
x_2
\\
ea
\end{array}
\right)
\end{eqnarray}
\tag{2-10}
\]
なお、ピストンピンはシリンダ中心軸上を運動するため、y座標はea一定となります。
(3)ピストン速度
(2-8)式を時間微分することで、Ψの時間微分関数\( \dot{\psi} \)が定まります。
\[
\dot{\psi}
=
\frac{R_{cra} \cos(\theta')}{L_{con} \cos \psi} \quad \dot{\theta}
\tag{2-11}
\]
あとは\( \bf{r_1} \)、\( \bf{r_2} \)を時間微分することで、ピストン速度\( \bf{ \dot{ r_2} } = \bf{ v_2 } \)を求めることができます。
\[
\begin{eqnarray}
& \bf{v_1} &
=
\bf{\dot{r_1}}
=
\dot{\theta} R(\theta' + \frac{ \pi }{ 2 } ) \bf{r_{cra}}
\\
& \bf{v_2} &
=
\bf{\dot{r_2}}
=
\bf{v_1} -
\dot{\psi} R( -\psi + \frac{ \pi }{ 2 } ) \bf{r_{con}}
\end{eqnarray}
\tag{2-12}
\]
ピストンのy座標は一定のため、ピストン速度はx軸方向のみ発生します
(つまり、y軸成分を計算する必要はありません)。
(4)ピストン加速度
(2-11)式を変形して
\[
\dot{\psi} L_{con} \cos \psi
=
\dot{\theta} R_{cra} \cos(\theta + \theta_o)
\]
上式を時間微分すると次式を得ます。
\[
\ddot{\psi}
=
\frac
{ R_{cra} ( \ddot{ \theta } \cos ( \theta + \theta_o ) - \dot{\theta}^2 \cos(\theta + \theta_o) ) }
{ L_{con} \cos \psi }
\qquad
+ \dot{ \psi }^2 \tan \psi
\]
クランクが等速円運動を行うとき\( \ddot{\theta} = 0 \)なので、上式は次のようになります。
\[
\ddot{\psi}
=
\frac
{ \dot{\theta}^2 R_{cra} \cos(\theta + \theta_o) }
{ L_{con} \cos \psi }
\quad + \dot{ \psi }^2 \tan \psi
\tag{2-13}
\]
あとは、(2-12)式を時間微分することで、ピストン加速度\( \bf{ \ddot{ r_2} } = \bf{ a_2 } \)を求めることができます。
\[
\begin{eqnarray}
& \bf{a_1} &
=
\bf{ \ddot{r_1} }
=
\left\{
\ddot{\theta} R( \theta + \theta_o + \frac{ \pi }{ 2 } )
-
\dot{\theta}^2 R ( \theta + \theta_o )
\right\}
\bf{r_{cra}}
\\
& \bf{a_2} &
=
\bf{\ddot{r_2}}
=
\bf{a_1} -
\left\{
\ddot{\psi} R( -\psi + \frac{ \pi }{ 2 } )
-
\psi^2 R( -\psi)
\right\}
\bf{r_{con}}
\end{eqnarray}
\tag{2-14}
\]