gijyutsu-keisan.com

1．機構の設計

1．1．リンクとは？

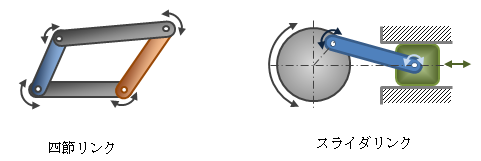
リンク（Link）には“連結”という意味があります。 機械要素におけるリンクとは、 機械システムを構成する部品間を連結する役割を担い、 さらに、連結された部品がその連結部において 回転やすべり運動を行うもののことを言います。 このリンクを用いて構成される装置をリンク装置と呼びます。 例えばリンク装置とは次のようなものが該当します。
図1－1　リンク装置の例
図1－1　リンク装置の例

リンク装置の目的は、主に機械的な入力を異なる出力に変換することにあります。
さて、リンクの話では“対偶”という言葉がつきものです。 この対偶とは、ペア（Pair）のことで、リンクが対になっていることを表します。 リンク装置の最小形が対偶であり、すべてのリンク装置はこの対偶の単位に分解できます。

2．リンクの設計フロー

リンク装置の目的は前章でも述べたように、機械的な入力を異なる出力に変換することです。 この目的を達成するために、次の主な課題を解決していくことがリンク設計の肝になります。
  1. 入力軌跡に対する出力軌跡の決定
  2. 入力負荷に対する出力負荷の決定
  3. リンク装置の構成部品の強度保証
  4. リンク装置の変形を考慮した補正

（1）は幾何学的拘束条件、つまり図形的に決定されます。 （2）はリンク装置構成部品の運動方程式によって導出されます。 （3）（4）は（2）によって求められたリンクに発生する荷重から材料力学的に導出されます。
その他、使用環境（温度、雰囲気、設置条件など）、作動音等の公害、安全性、メンテナンス性、 コストを考慮に入れて設計を行います。 特に機構を有する装置は安全性に特に注意を払う必要があります。 ここで、リンク装置の設計フロー概要（例）を以下に示します。
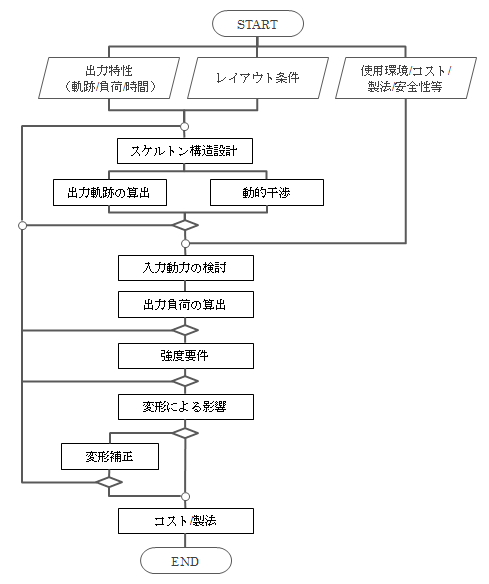
図2－1　リンク装置の設計フロー概要（例）
図2－1　リンク装置の設計フロー概要（例）

3．出力軌跡の決定

リンク装置でまず最初に決めるのが、 リンク装置によってどういった動き、つまり出力軌跡を得たいか？になります。
まずはじめにリンク構造の骨格を検討します。 各リンク連結部（節点）の配置と、その周りの自由度（並進自由度、回転自由度）を仮決定します。 このとき、リンクの軌跡を検討する上で最低限必要な情報のみで検討を行います。 これは節点を点、リンクを節点間をつなぐ線で表現したスケルトン構造によって行います。
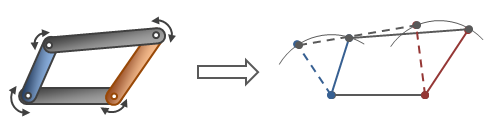
図3－1　リンク・スケルトン構造検討
図3－1　リンク・スケルトン構造検討
次に、その構造によって得られる出力軌跡を算出します。 出力軌跡を決定する際、リンクは剛体と仮定して幾何学的拘束条件をもとに計算します。 ここでは四節リンクとスライダクランク機構の出力軌跡を例として求めてみます。
現在作成中です。申し訳ありません。しばらくお待ちください。

以上のような例からもわかるように、幾何学的拘束条件を明確にし、 あとは図形の問題として処理できれば（実はコレが非常に難しい）、出力軌跡は算出されます。 また、特に三次元空間における運動の軌跡を求める際は、 座標変換（行列変換）を活用することで、計算を楽に行えるようになります。
さて、仕様から決まる必要作動時間をこの出力軌跡に対して定義すれば、 リンク各部の速度、加速度を決定することができます。 これにより、次章で必要となる各リンクの運動方程式を導出することが可能になります。

4．出力負荷の決定

出力軌跡位とリンク各部の速度、加速度が定まったので、 今度は装置の仕様能力を決定する因子となる出力負荷を決定します。
入力条件を設定すれば、
  • 速度、加速度が定まっていること
  • 幾何学的な条件が定まっていること

から、各部品の運動方程式を立てることで、各節点に発生する荷重を求めることができます。 これを行うことで自動的に出力負荷は定まります。
しかしながら、この運動方程式の導出は構造が複雑になればなるほど非常に難しいものになります。 運動方程式の導出は、一般的には次の2通りになります。
（1） ニュートン力学に従って、図式的に力のベクトルを描画しながら運動方程式をたてる
（2） 通常入力条件（動力）はエネルギーの単位で指定されること、 複雑な力ベクトルの関係図を描かなくても解析的（算術的かつ機械的）に運動方程式が立てられる ラグランジュ方程式（解析力学）を用いる

（2）のラグランジュ方程式を用いる場合、装置内に発生するエネルギーがすべて特定できれば （これは力学的なものだけでなく、電気的、熱的なものを含め）、 あとは座標の偏微分による算術的な処理によって運動方程式が簡単に立てられます。 しかしながら、ラグランジュ方程式はあくまで運動方程式を簡単に導出する方法であって、 その解が簡単に得られることを保証するものではありません。時として、 面倒でも（1）の図解法によって考察、計算する方がかえって結果を早く得られる場合があることを 念頭に置いておく必要があります。

5．強度と変形

4章で各節点に働く荷重が決まるので、それをもとに各リンクや節点に生じる応力、 変形を算出することができます。 しかし、実際はリンク部品の形状が複雑であったり、 前章の運動方程式を手計算的に解くのが困難な場合が多々あります。
もし金銭的余裕があるならば、動解析ツールといったCAEの導入を検討してみるのが良い、と考えます。 適切なモデルの作成と拘束条件の設定によって、リンクの出力軌跡や負荷から、 各節点やリンクの強度・変形（現状では弾性論の範囲が限界のようですが） を同時に評価できるようになります。
例）
ただ、このようなソフトウエアは決して安くはありません。 その場合は手計算で解くより他ありません。
この場合は、計算間違いを極力減らす努力をしていかなければなりません。 極力検討モデルを簡略化して行うことが大前提ですが、 その場合設計的なマージンが含まれる方向にモデルを簡略化しなければなりません。 ただし、設計的観点で相反するような事象は多々あります。そのとき何を優先させるか？は設計者の判断に委ねられます。 設計者はきちんとした思想と信念を持っていなければ、こういった時に判断に苦慮することになります。

6．リンク設計の課題

これまでは、ここで述べる課題については一切触れてきませんでした。 その理由は、リンク設計全体の概要をまずは捉えておきたかったためです。
ここで、新たなリンク設計の課題を挙げます。
リンク機構は節点において必ず荷重が発生します。 あるリンクに2つの荷重が2つの節点にそれぞれ作用したとき、 その荷重の作用線がお互い逆向きに1直線になることがあります。
図6－1　節点荷重のつり合い
図6－1　節点荷重のつり合い

こうなるとリンクは完全につりあってしまい、動けなくなります。 このような位置をリンク機構の死点と呼びます。 この死点上で入力負荷を与え続けると、装置の破損等の危険が生じます。
またこれとは逆に、リンクの運動に方向性がなくなる点が存在することがあります。 例えば右回りに動くように設計した装置がある状態で停止したとします。 装置が再度動き出そうとするとき、左右どちらへ動けばよいかわからないような点が存在する場合があります。 このような点を思案点と呼びます。これは完全拘束されていない、 自由度に対する入力因子の不足した状態である、と言えます。
以上の問題を洗い出すためには、結局軌跡の算出と運動方程式が重要な役割を担います。

参考文献

▲