1.等価慣性モーメント
等価慣性モーメントとは、電動機(モータ)に加わる負荷のうち、ギア等の物体が持つ慣性モーメントを電動機回転軸に対する慣性モーメントとして算出するものです。ここでは、下図の例をもとに等価慣性モーメントを算出してみます。 等価慣性モーメントを求めるのに必要となるパラメータも下図で設定します。 ただし、各部品の各回転軸周りの慣性モーメントをJk、歯数をzk (ピッチ半径をrk)、回転角をθkとします。 また、歯面接触部に発生する力をFk-1kとします。
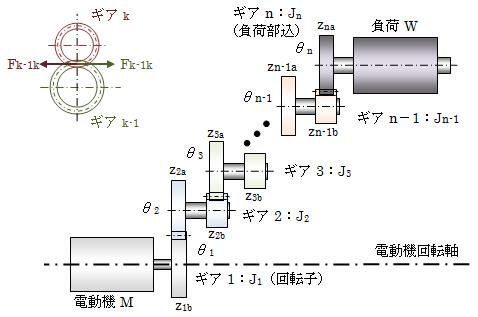
図1-1 電動機の減速機付き負荷
電動機の発生トルクをT、負荷部に発生するトルクをWとして、各軸周りの運動方程式を書いていきます。| 回転軸1(電動機回転軸) | : | \( T = J_2 \ddot{\theta_1} + r_{1b} F_{12} \) |
| 回転軸2 | : | \( J_2 \ddot{\theta_2} = r_{2a} F_{12} - r_{2b} F_{23} \) |
| 回転軸3 | : | \( J_3 \ddot{\theta_3} = r_{3a} F_{23} - r_{3b} F_{34} \) |
| ・・・ | ||
| 回転軸n-1 | : | \( J_{n-1} \ddot{\theta_{n-1}} = r_{(n-1)a} \ F_{(n-1)(n-2)} \ - r_{(n-1)b} \ F_{(n-1)n} \) |
| 回転軸n(負荷部) | : | \( r_{na}F_{(n-1)n} = J_n \ddot{\theta_n} + W\) |
\[
\begin{eqnarray}
& F_{(n-1)n}
& = &
\frac{1}{r_{na}} ( J_n \ddot{\theta_n} + W)
\\
\\
& F_{(n-2)(n-1)} \quad
& = &
\frac{1}{r_{(n-1)a}} ( J_{(n-1)} \ \ddot{\theta_{(n-1)}} \ + r_{(n-1)b} \ F_{(n-1)n} \ )
\\
& & = &
\frac{1}{r_{(n-1)a}} \Bigl \{ J_{(n-1)} \ \ddot{\theta_{(n-1)}} \ + \frac{r_{(n-1)b}}{r_{na}} \ ( J_n \ddot{\theta_n} + W ) \Bigr \}
\\
\\
& F_{(n-3)(n-2)} \quad
& = &
\frac{1}{r_{(n-2)a}} ( J_{(n-2)} \ \ddot{\theta_{(n-2)}} \ + r_{(n-2)b} \ F_{(n-2)(n-1)} \quad )
\\
& & = &
\frac{1}{r_{(n-2)a}} \Bigl \{ J_{(n-2)} \ \ddot{\theta_{(n-2)}} \ +
\frac{r_{(n-2)b}}{r_{(n-1)a}} \ J_{n-1} \ddot{\theta_{n-1}} +
\frac{r_{(n-2)b} \ \cdot r_{(n-1)b} }{r_{(n-1)a} \ \cdot r_{na}} \ J_n \ddot{\theta_n}
\Bigr \}
\\ & & & \qquad
+ \frac{r_{(n-2)b} \ \cdot r_{(n-1)b}}{r_{(n-2)a} \ \cdot r_{(n-1)a} \ \cdot r_{na}} \ W
\\
& & \cdots
\\
& F_{12} \quad
& = &
\frac{1}{r_{2a}} ( J_2 \ddot{\theta_2} + r_{2b} \ F_{23} )
\\
& & = &
\frac{1}{r_{2a}} \Bigl \{ J_2 \ddot{\theta_2} + \frac{r_{2b}}{r_{3a}} J_3 \ddot{\theta_3} +
\cdots
+ \Bigl( \frac{r_{2b} \cdots r_{(n-1)b}}{r_{3a} \cdots r_{na}} \ J_n \ddot{\theta_n} \Bigr) \Bigr \}
\\
& & & \qquad
+ \frac{1}{r_{2a}} \frac{r_{2b} \cdots r_{(n-1)b}}{r_{3a} \cdots r_{na}} \ W
\\
\\
& T
& = &
J_1 \ddot{ \theta_1 } L r_{1b} F_{12}
\\
\\
& & = &
\Bigl \{ J_1 \ddot{ \theta_1 } + \frac{r_{2b}}{r_{2a}} J_2 \ddot { \theta_2 } + \cdots
+ \Bigl( \frac{r_{1b} \cdots r_{(n-1)b}}{r_{2a} \cdots r_{na}} \ J_n \ddot{\theta_n} \Bigr) \Bigr \}
\\
\\
& & & \qquad
+ \frac{r_{1b} \cdots r_{(n-1)b}}{r_{2a} \cdots r_{na}} \ W
\tag{1-1}
\end{eqnarray}
\]
また、角軸の回転角には次のような関係が成り立ちます。\[
\begin{eqnarray}
\theta_1 : \theta_2
& = &
z_{2a} : z_{1b}
\quad
\leftrightarrow
\quad
\theta_2
=
\frac{z_{1b}}{z_{2a}} \theta_1
\\
\theta_2 : \theta_3
& = &
z_{3a} : z_{2b}
\quad
\leftrightarrow
\quad
\theta_3
=
\frac{z_{2b}}{z_{3a}} \theta_2
\\
\cdots
\\
\theta_{n-1} : \theta_n
& = &
z_{na} : z_{(n-1)b}
\quad
\leftrightarrow
\quad
\theta_n
=
\frac{z_{(n-1)b}}{z_{na}} \ \theta_{(n-1)}
\end{eqnarray}
\]
回転角の関係式からθnをθ1で表すことができます。\[
\theta_n
=
\frac{ z_{(n-1)b} \ \cdots z_{2b} \cdot z_{1b}}{z_{na} \cdots z_{3a} \cdot z_{2a}} \quad \theta_1
\tag{1-2}
\]
また、歯数の比と歯車径の比は近似的に等しいので、\[
\frac{z_{(k-1)b}}{z_{ka}} \ \fallingdotseq \frac{r_{(k-1)b}}{r_{ka}}
\]
の関係から、これらを(1-1)式に代入して次の結果が得られます。\[
T
=
\Bigl \{ J_1 + \Bigl( \frac{z_{1b}}{z_{2a}} \Bigr)^2 J_2
+ \cdots + \Bigl( \frac{z_{1b} \cdots z_{(n-1)b}}{z_{2a} \cdots z_{na}} \ \Bigr)^2 J_n \Bigr\} \ddot{\theta_1}
+ \frac{z_{1b} \cdots z_{(n-1)b}}{z_{2a} \cdots z_{na}} \ W
\tag{1-3}
\]
この式は、電動機の回転軸周りに発生する慣性力と、その軸換算での負荷トルクの合計が、電動機の発生するトルクと釣り合うことを表しています。
この角加速度の係数は、各ギアの慣性モーメントを電動機の回転軸周りの慣性モーメントとして扱っています。
つまり、各ギアの軸換算を行った慣性モーメント=等価慣性モーメントを足し合わせたもの、ということになります。\[
J_{eq}
=
J_1 + \Bigl( \frac{z_{1b}}{z_{2a}} \Bigr)^2+ \cdots + \Bigl( \frac{z_{1b} \cdots z_{(n-1)b}}{z_{2a} \cdots z_{na}} \ \Bigr)^2 J_n
\tag{1-4}
\]
(1-4)式から各軸周りの等価慣性モーメントに分解すると、次のように表せます。回転軸nの等価慣性モーメント
\[
\Bigl( \frac{z_{1b} \cdot z_{(n-1)b}}{z_{2a} \cdot z_{na}} \ \Bigr)^2 J_n
\tag{1-5}
\]
このように等価慣性モーメントは、各ギアの回転軸周りの慣性モーメントに減速比の二乗を掛けたものになります。


