gijyutsu-keisan.com

1．三角測量の基本式

三角測量は、角度と距離の次のような関係から、測定点の位置を割り出す手法です。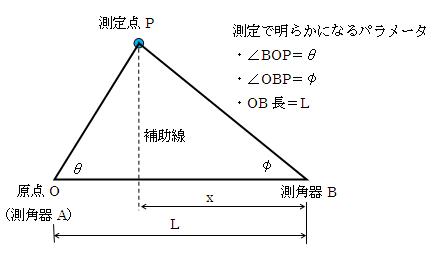
図1－1　三角測量の基本原理
図1.1－1　三角測量の基本原理
\[ x\tan \phi = (L-x) \tan \phi \leftrightarrow x = \frac{ L \tan \theta} { \tan \theta + \tan \phi } \]
ここで次の公式を用いるとOPの長さは、
\[ \tan \theta + \tan \phi = \frac{ \sin ( \theta + \phi ) } { \cos \theta \cos \phi } \] \[ | \overrightarrow{ OP } | = \frac{ L \sin \phi } { \sin ( \theta + \phi ) } \]
よって、測定点Pの位置は次のように表せます。
\[ \overrightarrow{ OP } = \left( \begin{array}{c} \displaystyle\frac{ L \sin \phi \cos \theta } { \sin ( \theta + \phi ) } \\ \displaystyle\frac{ L \sin \phi \sin \theta } { \sin ( \theta + \phi ) } \end{array} \ \ \right) \tag{1-1} \]

2．三角測量の準備

三角測量は、測角器であるセオドライト（よく土木測量で使用されている望遠鏡のようなもの）2台と、精密に寸法管理されたスケールバーによって行われます。 セオドライトは、水平角と鉛直角の2つの角度を精密に測定する機械です。 測定は、まず座標系の設定から行います。

2．1．座標系の設定

  1. セオドライト2台をある適当な位置に置き、それぞれの鉛直を出します。
  2. 1台のセオドライトを測定原点とすることで、鉛直軸（Z軸）が決定します。
  3. 2台のセオドライトをお見合いさせたときに出来る線分から、鉛直軸に直角な成分を一つの水平軸（X軸）に決定します。
  4. 自動的に3つめの軸（Y軸）が決定します。
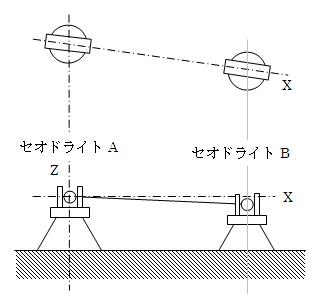
図2.1－1　測定座標の定義
図2.1－1　測定座標の定義
これまでは、座標系を定義しただけですので、図2.1－1でいう“L”（セオドライト間距離）が明確になっていません。 そこで、基準長さLを精確に測定し、測角と距離の関係を決定します。

2．2．基準長さの設定

ここでは計算を簡単にするため、高さ同一面内での測定とします （実際は、そんなことはありえないので、高さずれがわかる面で同じように計算すればよいことになります）。
  1. 超精密に長さ管理されているスケールバーを、セオドライト2台から見えるよう、適当な位置に置きます。
  2. スケールバーには測定ポイントが2点ありますので、その2点を2台のセオドライトで測角します。 このとき、セオドライトAとBが同じポイントを見たときの角度を測ることになります。 そのときのそれぞれの角度が後で重要になってきます。 当然ながら、見ているポイントがずれている場合は、それがそのまま測定誤差として上乗せされます。
  3. （1－1）式を用いて、Lがわかっているものとしてスケールバーの長さSを決める方程式を作ります。
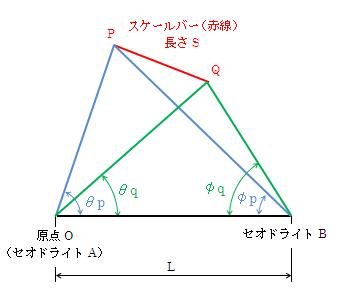
図2.2－2　基準長さLの決定
図2.2－2　基準長さLの決定
\[ \begin{eqnarray} \left\{ \begin{array}{l} \overrightarrow{ OP } = \left( \begin{array}{c} \displaystyle\frac{ L \sin \phi_p \cos \theta_p } { \sin ( \theta_p + \phi_p ) } \\ \displaystyle\frac{ L \sin \phi_p \sin \theta_p } { \sin ( \theta_p + \phi_p ) } \end{array} \ \ \right) \\ \overrightarrow{ OQ } = \left( \begin{array}{c} \displaystyle\frac{ L \sin \phi_q \cos \theta_q } { \sin ( \theta_q + \phi_q ) } \\ \displaystyle\frac{ L \sin \phi_q \sin \theta_q } { \sin ( \theta_q + \phi_q ) } \end{array} \ \ \right) \end{array} \right.\end{eqnarray} \tag{2.2-1} \]
ここで、パラメータa、bを
\[ a = \displaystyle\frac{ \sin \phi_p } { \sin ( \theta_p + \phi_p ) } \quad , b = \frac{ \sin \phi_q } { \sin ( \theta_q + \phi_q ) } \]
と設定すれば、（2.2－1）式は次のように書き換えられます。
\[ \begin{eqnarray} \left\{ \begin{array}{l} \overrightarrow{ OP } = \left( \begin{array}{c} aL \cos \theta_p \ \\ aL \sin \theta_p \ \end{array} \right) \\ \overrightarrow{ OQ } = \left( \begin{array}{c} bL \cos \theta_q \ \\ bL \sin \theta_q \ \end{array} \right) \end{array} \right.\end{eqnarray} \tag{2.2-2} \]
今、セオドライトA、B間の距離Lを精確に測りたいので、スケールバーの長さSと（2.2－2）式との関係が明らかになれば、Lを求めることが出来ます。 PQベクトルは次のように表せます。
\[ \overrightarrow{ PQ } = L \left( \begin{array}{c} b \cos \theta_q - a \cos \theta_p \quad \\ b \sin \theta_q - a \ sin \theta_p \quad \end{array} \right) \]
また、PQベクトルの長さがスケールバーの長さSになりますので、
\[ \begin{align*} | \overrightarrow{ PQ } |^2 &= L^2 \{ ( b \cos \theta_p - a \cos \theta_q )^2 +( b \sin \theta_p - a \sin \theta_q )^2 \} \\ & = L^2 \{ a^2 + b^2 - 2ab ( \cos \theta_p \cos \theta_q + \sin \theta_p \sin \theta_q ) \} \\ & = L^2 \{ a^2 + b^2 - 2ab ( \cos ( \theta_p - \theta_q ) \} \\ & = S^2 \end{align*} \]
さらに
\[ c^2 = a^2 + b^2 - 2ab \cos (\theta_p - \theta_q) \]
とおけば、S2=（cL）2が成立し、Sは長さのためS＞0から、
\[ S = cL \leftrightarrow L = \frac {S}{c} \tag{2.2-3} \]
以上より、2台のセオドライト間の距離Lが、測角データとスケールデータで精確に決定できることがわかりました。 前にも述べましたように、計算を簡単にするため、高さ（鉛直方向）のずれについてはここでは考慮していませんが、同様にして求めることが出来ます。

3．非接触三次元計測

非接触三次元測定の肝は、超精密に管理された一つの長さパラメータと座標系の設定にあります。 ここをいい加減に行えば、測定誤差は大きくなり、使えないデータとなってしまいます。 1章で述べた計算式を元に、どのように測定すれば測定誤差を小さく出来るかを検討すること ＝パラメータの感度解析が重要になります。
最後に、非接触三次元測定は、1項で述べたような三角測量の原理を、 今までの土木測量や大規模構造体のアライメント調整の範囲から、 一般的な測定物に対象を広げたものです。 非接触三次元計測によって被測定物の3次元形状データを取り込めるようになったのは、 ハードとソフトの進歩によるものが大きいと考えられます。 コンピュータの演算処理が格段に早くなったおかげで、 非常に簡単に様々な形状の3Dデータを作成できるようになりました。 また、3D－CADの普及により、取り込んだデータを手軽に見たり、加工したり出来るようになりました。 この被接触三次元計測の技術は計測だけでなく、医療（手術ロボット）などにも応用されています。

参考文献

▲