gijyutsu-keisan.com
ニュートン法は、関数化された方程式の解を、数値計算によって近似的に求める方法です （ニュートン・ラフソン法とも呼びます）。 幾何学的に言えば「曲線の交点を求める方法」とも言えます。 ニュートン法は、一変数関数\( f(x) \)でも多変数関数\( f(x_1,x_2,・・・,x_n) \)でも、どちらにも適用できます。
まずはニュートン法のロジックを理解するために、簡単な一変数関数から話を進めます。

Excelによるニュートン法の計算方法については、 Excelによるニュートン法の計算 で説明します（VBAを利用しています）。

1．一変数のニュートン法

1．1．一変数のニュートン法手順

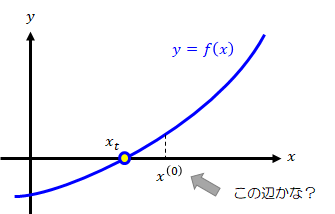
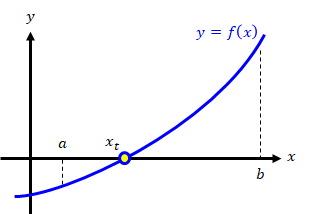
関数\( y=f(x) \)が与えられたとき、ニュートン法を用いて\( f(x)=0 \)の解を求める手順を示します。 これは、関数\( y=f(x) \)と\( y=0 \)の二つの曲線の交点を求めることに他なりません。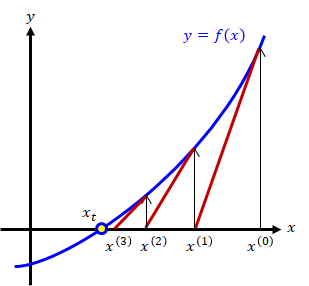
ニュートン法の計算
図1－1　ニュートン法の計算
上図と一緒に各Stepの内容を確認してください。

Step1：

\( f(x)=0 \)の真の解\( x_t \)の近傍点\( x^{(0)} \ \)を適当に決めます （\( x_t \)は未知なので\( y=f(x) \)をグラフ化してを決めるのが妥当です）。

Step2：

点\( ( x^{(0)} , f(x^{(0)} \ ) ) \)での\( f(x) \)の接線を求め、その接線とx軸との交点を\( x^{(1)} \ \)とします。 接線は\( f(x) \)を\( x^{(0)} \)でテイラー展開し、その一次近似をとることで決まります。
\[ y = f(x^{(0)}) + f'(x^{(0)}) \ ( x - x^{(0)} ) \tag{1.1-1} \]
さらに、上式から\( x^{(1)} \ \)が求まります。
\[ x^{(1)} = x^{(0)} - \frac{ f(x^{(0)}) }{ f'(x^{(0)}) } \tag{1.1-2} \]

Step3：

前Stepとの解の変化が微小値\( \epsilon \)（収束判定値）より小さければ、\( x^{(1)} \ \)を\( f(x)=0 \)の近似解とします。
\[ | x^{(1)} - x^{(0)} | < \epsilon \tag{1.1-3} \]
上式を満たさない場合は、解の変化が\( \epsilon \)より小さくなるまで、\( x^{(2)},x^{(3)},\cdots \)を求めて差分を評価する操作、Step2、Step3、・・・を繰り返します。
以上の手順から、ニュートン法は次の二つの計算を繰り返すだけです。
\[ x^{(i+1)} = x^{(i)} - \frac{ f(x^{(i)}) }{ f'(x^{(i)}) } \tag{1.1-4} \] \[ | x^{(i+1)} - x^{(i)} | < \epsilon \tag{1.1-5} \]
なお、収束判定値を小さくするほど真の解\( x_t \)に近づきますが、その分計算回数は増えます。
また、ニュートン法を適用できる関数の条件としては“\( f(x) \)は微分可能”、“計算対象範囲で\( f''(x) \)の符号は一定”の二つです。

1．2．ニュートン法を使った例

（1）“\( \sqrt{2} \ \)”の計算

一般的な例ではありますが、“\( \sqrt{2} \ \)”を計算してみます。
まず、関数として
\[ f(x) = x^2 - 2 \]
を準備します。この関数とx軸との交点を求めれば、つまり\( f(x) = 0 \)の解が\( \sqrt{2} \ \)となります。
（1.1-4）式を見ると、\( f(x) \)の一階微分が必要になります。
\[ f'(x) = 2x \]
ここで初期解\( x^{(0)} = 1 \)をとしてみると、
\[ \begin{eqnarray} & x^{(1)} & = 1 - \frac{-1}{2} = 1.5 \\ & x^{(2)} & = 1.5 - \frac{ 0.25 }{ 3} = 1.41666\cdots \end{eqnarray} \]
という風になり、例えば計算を4回繰り返せば
\[ x^{(4)} = 1.4142135623\cdots \]
が得られます。

（2）“\( x^2 - 4 = 0 \)”の計算

（1）の例とほとんど同じですが、ここでは初期値を変えることによる影響を見ていきます。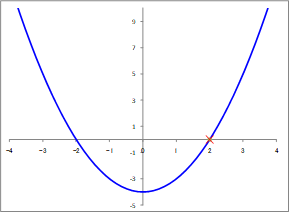
x^2 - 4 = 0 上図3－1からもわかるように、\( f(x)=0 \)の解はx=±2になります。
ここで、初期値\( x^{(0)} = 3 \)として計算してみると、反復計算5回目で“x=+2”という解を得ることができます。
表1.3-1　\( x_0 = 3 \)での\( f(x)=0 \)の解
x^2 - 4 = 0
次に、初期値\( x^{(0)} = -3 \)として計算してみると、反復計算5回目で“x=-2”という解を得ることができます。
表1.3-2　\( x_0 = -3 \)での\( f(x)=0 \)の解
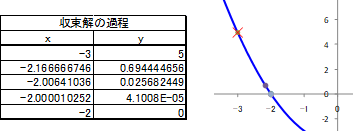x^2 - 4 = 0 最後に、初期値\( x_0 = 0.01 \)として計算してみると、
表1.3-3　\( x_0 = 0.01 \)での\( f(x)=0 \)の解
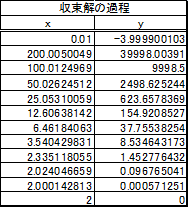x^2 - 4 = 0 この場合、反復計算は12回必要になりました。 通常、初期値を変えれば反復計算の回数も変わります。

1．3．ニュートン法の証明

<命題>

区間[a,b]において、\(f(x)\)は二階以上微分可能とします。 このとき、\( f''(x) > 0 、f(a) < 0, f(b) > 0 \)ならば\( x^{(0)} = b \)とおいて、数列
\[ x^{(i+1)} = x^{(i)} - \frac{ f(x^{(i)}) }{ f'(x^{(i)}) } \]
は\( f(x) = 0 \)のただ一つの解\( x_t \)に収束します。

証明 ******************************

\( f''(x) > 0 \)なので、\( f'(x) \)は単調増加、は下に凸の関数になります。 また、\( f(a) < 0, f(b) > 0 \)の条件とあわせれば、\( f(x) = 0 \)の解\( x_t \)は[a,b]にただ一つ存在します。
ニュートン法の計算
ここで[\(x_t \),b]に着目します。 \( f'(c) = 0 \)を満たすcがこの区間内に存在すると仮定すると、\( f(c) \)は関数\( f(x) \)の最小値をとります。 従って、\( f(x_t) = 0 > f(c) \)となります。 \( f(b) > 0 \)から[c,b]の範囲で\( f(x) = 0 \)は解を持つことになりますが、これは前述のただ一つの解の存在と矛盾します。
次に、[\(x_t \),b]で\( f'(x) < 0 \)とすれば、\( f(x) \)は単調減少となり、\( f(x_t) = 0 \), \( f'(x) > 0 \)と矛盾します。
以上から、[\(x_t\),b]で\( f'(x) > 0 \), \( f(x) \)は単調増加となります。
このとき、数列\( x^{(n)} \)は\( f(x^{(n)})/f'(x^{(n)}) > 0 \)であるから単調減少となります。
さらに、の極限を\( \alpha \)とすると、
\[ \alpha = \alpha - \frac{ f(\alpha) }{ f'(\alpha) } \ \Leftrightarrow \ f(\alpha)=0 \]
となって、\( \alpha \)は\( f(x) = 0 \)の解となります。 つまり、数列\( x^{(n)} \)は\( x_t \)に収束します。

****************************** おわり

1．4．ニュートン法の問題点

（1）関数\( f(x) \)の一階微分を自分で設定する必要があります。

\( f(x) \)が複雑な場合や、\( f(x) \)が自動的にモデル化されるような場合、対応は困難です。

（2）解が収束するとは限りません。

例えば下図のような条件を満たしてしまうと、無限ループ化し、解は得られません。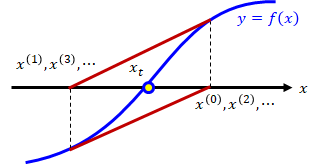
無限ループ このような場合、初期解を少しずらすことで解決することがあります。

他に発散する場合もあります。 これは\( f'(x) = 0 \)となるxの値を初期値とした場合で、その接線はx軸と交わることはありません。 つまり初期値から計算が進展せず、\( f(x) = 0 \)の解を求めることはできません。
発散

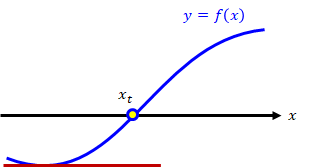
（3）初期解の決め方がはっきりしません。

真の解の近傍、と言われても、真の解は不明なため決めようがありません。 せいぜい関数をグラフ化してみて決めるぐらいしかありません。
初期解

参考文献

▲