QR分解
3．ハウスホルダー法
ハウスホルダー法によるm×n行列A（m≥n）のQR分解は、1列ずつ対角成分より下の成分を0にしていくことで実行される方法です。\[
\begin{pmatrix}
* & * & * & *
\\
* & * & * & *
\\
* & * & * & *
\\
* & * & * & *
\end{pmatrix}
\rightarrow
\begin{pmatrix}
* & * & * & *
\\
0 & * & * & *
\\
0 & * & * & *
\\
0 & * & * & *
\end{pmatrix}
\rightarrow
\begin{pmatrix}
* & * & * & *
\\
0 & * & * & *
\\
0 & 0 & * & *
\\
0 & 0 & * & *
\end{pmatrix}
\rightarrow
\begin{pmatrix}
* & * & * & *
\\
0 & * & * & *
\\
0 & 0 & * & *
\\
0 & 0 & 0 & *
\end{pmatrix}
\]
このとき用いられる変換がハウスホルダー変換になります。
3．1．ハウスホルダー変換
ハウスホルダー変換は鏡像変換とも呼ばれ、幾何学的に次のような意味を持ちます。まずは次のようにパラメータを設定します。
- 空間上の任意の位置ベクトル\( \bf{ x } \in R^{ n \times 1 } \)
- 原点を含む平面Uの法線ベクトル\( \bf{ u } \in R^{ n \times 1 } \)
\[
\bf{ x' } = ( I - 2 \bf{ u u^{t} } ) \bf{ x }
\tag{3.1-1}
\]
で定義します。
このとき、\( \bf{ u u^{t} } \)は正方行列を表します
（∵行列サイズに対して（n×1）×（1×n）=（n×n））。以上のパラメータを図示すると下図のようになります。
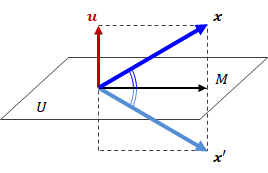点\( \bf{ x' } \)と\( \bf{ x } \)を結ぶ直線は
\[
\bf{ x } - \bf{ x' }
=
\bf{ x } - ( I - 2 \bf{ u u^{t} } ) \bf{ x }
= 2 \bf{ u u^{t} } \bf{ x }
\tag{3.1-2}
\]
で表せます。
ここで\( \bf{ u^{t} } \bf{ x } \)はベクトル\( \bf{ u } \)と\( \bf{ x } \)の内積であるため、\( \bf{ u ( u^{t} } \bf{ x } ) \)は \( \bf{ u } \)のスカラー倍、つまり\( \bf{ x } - \bf{ x' } \)は \( \bf{ u } \)と平行であることがわかります。
さらに、\( \bf{ u } \)と\( ( \bf{ x } - \bf{ u u^{t} x } ) \)の内積を計算すると、
\[
\bf{ u }^t ( \bf{ x } - \bf{ u u^{t} x } )
=
\bf{ u^t } \bf{ x } - \bf{ u^t u u^{t} x }
= \bf{ u^t } \bf{ x } - \bf{ u^{t} x }
= 0
\\
\qquad ( \because \bf{ u^t u } = 1 )
\tag{3.1-3}
\]
が得られます。
この式から\( \bf{ u } \)と\( \bf{ x } - \bf{ u u^{t} x } \)は直交しており、その結果、\( \bf{ x } - \bf{ u u^{t} x } \)は平面U内にあることがわかります。
さらに（3.3-1）式から\( \bf{ u u^{t} x } = ( \bf{ x } - \bf{ x' } ) / 2 \)は\( \bf{ x } - \bf{ x' } \)の中点、つまり図中Mの点を表しています。
従って、「点\( \bf{ x' } \)は点\( \bf{ x } \)の平面Uに対して対称な点」であることがわかります。
以上の結果をもとに、（3.3-1）式の係数行列 を\( H \)とおいて、
\[
H
=
I - 2 \bf{ u u^{t} }
=
\begin{pmatrix}
& 1 - 2 u_1^2 & -2 u_1u_2 & \cdots & -2 u_1 u_n &
\\
& -2 u_2u_1 & 1 - 2 u_2^2 & \cdots & -2 u_2 u_n &
\\
& \vdots & \vdots & \ddots & \vdots &
\\
& -2 u_n u_1 & -2 u_nu_2 & \cdots & 1 - 2 u_n^2 &
\end{pmatrix}
\tag{3.1-4}
\]
をハウスホルダー変換または鏡像変換と呼びます。
定義式から\( H \)は明らかに対称行列です。
また\( H \)がユニタリ変換であることは、次の理由からわかります。
- 鏡像の鏡像は元に戻るため、\( H^{-1} = H \leftrightarrow H H = I \)
- \( H^t = I^t - ( \bf{ u u^t } )^t = I - ( \bf{ u u^t } ) = H \)であること（1）から\( H^t = H^{-1} \)
- （1）から\( 1 = \det{ ( H H ) } = \det{ H } \det{ H } \) \( \rightarrow \det{ H } = \pm 1\)
3．2．ハウスホルダー行列の決定
ハウスホルダー変換の性質は前節で述べた通りです。ここでは、ハウスホルダー行列の成分を具体的に決定する方法について説明していきます。
n次元ベクトル\( \bf{a} =( a_{1}, \cdots , a_{n} )^t \ \)について、i+1行目以降をすべて0にするためのハウスホルダー行列Hの決め方について説明します。
まずは次の計算を行います。
\[
\begin{eqnarray}
\left \{
\begin{array}{1}
s
=
\mathrm{ -sgn } \left( a_{i} \ \right)
\displaystyle \sqrt { \sum_{j=i}^{n} a_{j}^2 }
\quad ( sgn：a_{i}の符号 )
\\
\alpha
=
\sqrt { s \ ( s - a_{i} \ ) }
\end{array}
\right.
\end{eqnarray}
\tag{3.2-1}
\]
このとき、\( s=0 \)ならすでにi+1行目以降はすべて0になっているため、以降の計算は不要となり\( H = I \)とします。\( s \neq 0, \alpha \neq 0 \)の場合、\( s, \alpha \)を使ってベクトル\( \bf{u} \)を次のように定義します （\( s \neq 0, \alpha = 0 \)の場合は後述します）。
\[
\bf{ u }
=
\frac{1}{\alpha}
\left(
\begin{array}{c}
0
\\
\vdots
\\
0
\\
a_{i} - s
\\
a_{i+1}
\\
\vdots
\\
a_{n}
\end{array}
\right)
\tag{3.2-2}
\]
この\( \bf{u} \)を使って次の計算を行います。
\[
\bf{u}\bf{u^t}
=
\begin{pmatrix}
O & O
\\
O & U_{n-i}
\end{pmatrix}
\]
\[
U_{n-i}
=
\frac{1}{s(s-a_i)}
\begin{pmatrix}
(a_{i} - s)^2 & (a_{i} - s)a_{i+1} & (a_{i} - s)a_{i+2} &\cdots & (a_{i} - s)a_{n} &
\\
a_{i+1}(a_{i} - s) & a_{i+1}^2 & a_{i+1} \ a_{i+2} & \cdots & a_{i+1} \ a_{n} &
\\
a_{i+2}(a_{i} - s) & a_{i+2} \ a_{i+1} & a_{i+2}^2 & & \vdots
\\
\vdots & \vdots & & \ddots & a_{n-1}a_{n} &
\\
a_{n}(a_{i} - s) & a_{n}a_{i+1} & \cdots & a_{n}a_{n-1} & a_{n}^2 &
\end{pmatrix}
\tag{3.2-3}
\]
このとき、ハウスホルダー行列Hを次のように定義します。
\[
H = I - 2 \bf{u^t}\bf{u}
\tag{3.2-4}
\]
\( s \neq 0, \alpha = 0 \)、つまり\( s = a_{kk} \)の場合このままでは計算不能になります。
この場合、i+1～n行成分の中から絶対値最大の成分を探し出し、その行とi行成分を入れ替えるピボッティングを施すことで計算を続けることができます。
ピボッティング操作は、基本変形行列の交換行列によって行えます。
この交換行列もまたユニタリ行列なので、QR分解のプロセス内に用いても問題になりません。
最後に、ハウスホルダー変換によってn次元ベクトル\( \bf{a} =( a_{1}, \cdots , a_{n} )^t \ \)が、狙ったとおりi+1行目以降すべて0になることを確認してみます。 （そのようにハウスホルダー変換を定義したのでなるはずです）。
\[
\begin{eqnarray}
&
H \bf{a}
& =
\begin{pmatrix}
I_{i-1} & O
\\
O & I_{n-i}-U_{n-i}
\end{pmatrix}
\begin{pmatrix}
\bf{a_{i-1}}
\\
\bf{a_{n-i}}
\end{pmatrix}
\\
& & =
\begin{pmatrix}
\bf{a_{i-1}}
\\
\bf{a_{n-i}} - U_{n-i} \ \bf{a_{n-i}}
\end{pmatrix}
\end{eqnarray}
\tag{3.2-5}
\]
ハウスホルダー変換では、実際に計算するのはi行目以降になります。
\[
\begin{eqnarray}
&
U_{n-i} \ \bf{a_{n-i}}
& =
\frac{1}{s(s-a_i)}
\begin{pmatrix}
(a_{i} - s)^2 & (a_{i} - s)a_{i+1} & \cdots & (a_{i} - s)a_{n} &
\\
a_{i+1}(a_{i} - s) & a_{i+1}^2 & \cdots & a_{i+1} \ a_{n} &
\\
\vdots & \vdots & \ddots & \vdots &
\\
a_{n}(a_{i} - s) & a_{n}a_{i+1} & \cdots &a_{n}^2 &
\end{pmatrix}
\begin{pmatrix}
a_{i}
\\
a_{i+1}
\\
\vdots
\\
a_{n}
\end{pmatrix}
\\
\\
& & =
\frac{1}{s(s-a_i)}
\begin{pmatrix}
(a_{i} - s)^2 a_{i} + (a_{i} - s)a_{i+1}^2 + \cdots + (a_{i} - s)a_{n}^2 \quad &
\\
a_{i+1} a_{i} (a_{i} - s) + a_{i+1}^3 + \cdots + a_{i+1} \ a_{n}^2 &
\\
\vdots
\\
a_{n} a_{i} (a_{i} - s) + a_{n} a_{i+1}^2 + \cdots + a_{n}^3 &
\end{pmatrix}
\\
\\
& & =
\frac{1}{s(s-a_i)}
\begin{pmatrix}
(s-a_i) \{ (a_{i} - s) a_{i} + a_{i+1}^2 + \cdots + a_{n}^2 \} \quad &
\\
a_{i+1} \{ (a_{i} - s) a_{i} + a_{i+1}^2 + \cdots + a_{n}^2 \} &
\\
\vdots
\\
a_{n} \{ (a_{i} - s) a_{i} + a_{i+1}^2 + \cdots + a_{n}^2 \} &
\end{pmatrix}
\\
\\
\end{eqnarray}
\]
ここで、
\[
\begin{eqnarray}
& ( a_{i} - s ) a_i + a_{i+1}^2 + \cdots + a_{n}^2 \quad
& =
( a_{i} - s ) a_i + s^2 - a_i^2
\\
& & =
- ( s - a_{i} ) a_i + ( s- a_i )( s + a_i )
\\
& & =
s ( s - a_i ) &
\end{eqnarray}
\]
を用いれば、
\[
U_{n-i} \ \bf{a_{n-i}}
=
\begin{pmatrix}
( a_{i} - s )
\\
a_{i+1}
\\
\vdots
\\
a_{n}
\end{pmatrix}
\tag{3.2-6}
\]
が得られます。従って、これを（3.2-5）式に適用して
\[
\begin{eqnarray}
&
H \bf{a}
& =
\begin{pmatrix}
\bf{a_{i-1}} &
\\
\bf{a_{n-i}} - U_{n-i} \ \bf{a_{n-i}} &
\end{pmatrix}
& & =
\begin{pmatrix}
\bf{a_{i-1}}
\\
s
\\
\bf{o_{n-i-1}}
\end{pmatrix}
\end{eqnarray}
\]
となって、目的の結果が得られます。
3．3．ハウスホルダー法による数値計算
ここではハウスホルダー変換を用いたQR分解の計算手順について説明します。ハウスホルダー行列の定め方は前節で見た通りです。 それを前提に、ハウスホルダー法法の計算フローを以下に示します （なお、プログラムを記述する際、添数は0から始めるのが一般的ですので、それに基づき記述します）。
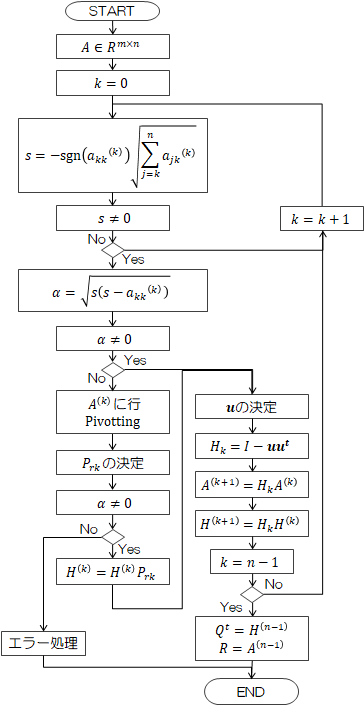QR分解では、通常Qを直接求める機会は多くありません。
連立方程式の解法では、その転置行列Qtを用います。
従って、上記フローではQではなくQtを求めるフローとなっています。また上記フローでは、行ピボッティングを入れていますが、列ピボッティングを用いても構いません。 ただし、列ピボッティングを使って連立方程式の解法に用いる場合は、列交換行列\( ( P_{c1} P_{c2} \cdots P_{cn} ) = T_c \)を記憶しておく必要があります （\( T_c \)はユニタリ行列）。
\[
Q^t A T_c = R
\
\rightarrow
\
A = QRT_c^t
\]
連立方程式に適用すると、
\[
\begin{eqnarray}
& A \bf{x} = \bf{y}
\\
& \rightarrow
QR ( T_c^t \bf{x} ) = \bf{y}
\\
& \rightarrow
R ( \bf{x'} ) = Q^t \bf{y}
\end{eqnarray}
\]
この形から後退代入によって\( \bf{x'} \)が求まるので、\( \bf{x} = T_c \bf{x'} \)が求まります。
