QR分解
1．QR分解
m×n行列A（m≥n）はm次ユニタリ行列Qとm×n上三角行列Rの積で表せます。 \[ A = QR \tag{1-1} \] これをQR分解と呼びます。Rは上三角行列なので、Aを係数行列とする連立方程式の解法にQR分解は適用できます。
\[
\bf{y} = A \bf{x} = QR \bf{x}
\\
\leftrightarrow
R\bf{x} = Q^t \bf{y}
\]
ここで、Qがユニタリ行列であることの特性、つまりQt=Q-1を活かしています。またこの特性から、ユニタリ行列Qのm次列ベクトルqi（i=1,・・・,n）は正規直交系を成します。
\[
Q^{t}Q
=
\begin{pmatrix}
q_1^tq_1 & q_1^tq_2 & \cdots & q_1^tq_m &
\\
\vdots & \vdots & \ddots & \vdots &
\\
q_m^tq_1 & q_m^tq_2 & \cdots & q_m^tq_m &
\\
\end{pmatrix}
=
\begin{pmatrix}
1 & & O &
\\
& \ddots & &
\\
O & & 1 &
\\
\end{pmatrix}
\]
\[
\therefore
q_i^tq_j
=
\delta_{ij}
\]
さて、QR分解の特徴は、LU分解に対して計算量は多いものの数値的に安定であることです。
そのため、最小二乗問題や固有値問題に用いられます。QR分解を行う方法として、次のものが挙げられます。
- （修正）グラム・シュミット法
- ハウスホルダー法
- ギブンス法
2．グラム・シュミット法
m×n行列AがQR分解可能であることは、グラム・シュミットの直交化法を用いれば証明できます。前節で挙げた（修正）グラム・シュミット法は、この証明法を数値計算に適用したものです。 そこでまずは、グラム・シュミットの直交化法について説明します。 具体的な数値計算の方法がわかればよい、ということであれば、この証明は読み飛ばして構いません （証明をスキップ）。
2．1．グラム・シュミットの直交化法
グラム・シュミットの直交化法とは次のようなものです。「数体K上の内積空間Vの、任意の部分空間は正規直交基底を持つ」
これがQR分解とどう結びつくか？というと、 m×n行列Aのm次元列ベクトル\( \bf{a_1},\cdots,\bf{a_n} \)が線形独立のとき、
- \( \bf{a_1},\cdots,\bf{a_n} (1\leq r \leq m ) \)は別の基底に置き換えられる
- その基底のうち、大きさ1、それぞれが直交する列ベクトル（正規直交系）を作ることができる
正規直交系によって構成される行列Uはユニタリ行列であり、その特性であるUt=U-1を活用できることが最大のメリットとなります。
またさらに言えば、正規直交系で構成される行列の代表格として挙げられるのは単位行列Iです。 実行列においてユニタリ行列Uはこの単位行列Iを回転変換したものに他なりません。
K上のm次元内積空間Vにおいて、\( \bf{a_1},\cdots,\bf{a_n} (1\leq r \leq m ) \)が線形独立のとき、次で定義する\( \bf{u_1},\cdots,\bf{u_n} \)は正規直交系（大きさ1で\( \bf{u_i}\) と\( \bf{u_j} \)（\( i \neq j \)）は直交）を成します。
\[
\begin{eqnarray}
& \bf{u_1} = \frac{\bf{a_1}}{|\bf{a_1}|} &
\\
& \bf{u_2} = \frac{\bf{a'_2}}{|\bf{a'_2}|} &
\quad , \
\bf{a'_2} = \bf{a_2} - ( \bf{a_2}^t \bf{u_1} ) \bf{u_1}
\\
\\
& & \cdots
\\
& \bf{u_n} = \frac{\bf{a'_n}}{|\bf{a'_n}|} &
\quad , \
\bf{a'_n} = \bf{a_n} - \sum_{k=1}^{n-1} ( \bf{a_n}^t \bf{u_i} ) \bf{u_i}
\end{eqnarray}
\]
と定義すると、
\[
K\bf{a_1} + \cdots + K\bf{a_n}
=
K\bf{u_1} + \cdots + K\bf{u_n}
\]
証明 ********************
＜前置き＞
まずは幾何学的な意味について考えてみます。定義から簡単にわかることは、\( \bf{u_1},\cdots,\bf{u_n} \)はすべて大きさ1のベクトルであることです。
次に、\( \bf{a'_2} \)について見てみます。
\[
\bf{a'_2} = \bf{a_2} - ( \bf{a_2}^t \bf{u_1} ) \bf{u_1}
\]
の中で\( \bf{a_2}^t \bf{u_1} \)はm次元ベクトルの内積を意味します。
\[
\begin{eqnarray}
& \bf{a_2}^t \bf{u_1}
& =
\begin{pmatrix}
a_{12}
\\
\vdots
\\
a_{m2}
\end{pmatrix}
(u_1, \cdots, u_m )
\\
& & =
a_{12}u_1 + \cdots + a_{m2}u_m
\end{eqnarray}
\]
ベクトルの内積は\( \bf{a_2} \)の\( \bf{u_1} \)方向成分の抽出を意味します。
つまり、下図中緑線になることがわかります。
すると、下図中青線が\( \bf{a'_2} \)になります。
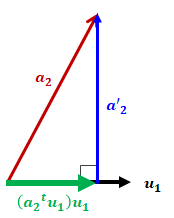その結果、\( \bf{a'_2} \)と\( \bf{u_1} \)は直交、\( \bf{a'_2}^t\bf{u_1}=0 \)を満たすことがわかります。
さらに、\( \bf{u_2} \)は\( \bf{a'_2} \)の大きさを1にしたものなので、\( \bf{u_2}^t\bf{u_1}=0 \)を満たします。
次に\( \bf{a'_3} \)について見ていきます。
\( \bf{a'_3} \)と\( \bf{u_2} \)、\( \bf{u_1} \)の内積についてそれぞれ計算します。 このとき、ベクトルの内積はあくまで係数であることに注意をすれば、
\[
\bf{a'_3}^t \bf{u_2}
=
\bf{a_3}^t\bf{u_2} - ( \bf{a_3}^t \bf{u_1} ) \bf{u_1}^t \bf{u_2} - ( \bf{a_3}^t \bf{u_2} ) \bf{u_2}^t \bf{u_2}
=
0
\]
\[
\bf{a'_3}^t \bf{u_1}
=
\bf{a_3}^t\bf{u_1} - ( \bf{a_3}^t \bf{u_1} ) \bf{u_1}^t \bf{u_1} - ( \bf{a_3}^t \bf{u_2} ) \bf{u_2}^t \bf{u_1}
=
0
\]
が得られます。
従って、\( \bf{u_3} \)は\( \bf{u_2} \)、\( \bf{u_1} \)と直交することがわかります。
以上の結果から、数学的帰納法を用いることで命題の証明はできます。
＜証明＞
\( r=1 \)のとき自明。 \( \bf{u_1},\cdots,\bf{u_{n-1}} \)が正規直交系で\[
K\bf{a_1} + \cdots + K\bf{a_{n-1}} = K\bf{u_1} + \cdots + K\bf{u_{n-1}}
\]
を満たすとします。
まず、\(\bf{a'_n} = \bf{o} \)とすると、
\[
\bf{a_n} =
\sum_{k=1}^{n-1}( \bf{a_n}^t \bf{u_k} ) \bf{u_k}
\in
K\bf{u_1} + \cdots + K\bf{u_{n-1}}
=
K\bf{a_1} + \cdots + K\bf{a_{n-1}}
\]
となって、\( \bf{a_1},\cdots,\bf{a_{n-1}},\bf{a_n} \)は線型従属となって仮定と矛盾します。
従って\(\bf{a'_n} \neq \bf{o} \)です。
次に、
\[
\begin{eqnarray}
( \bf{a'_n}^t \bf{u_i} )
& = &
( \bf{a_n}^t \bf{u_i} ) - \sum_{k=1}^{n-1}( ( \bf{a_n}^t \bf{u_k} ) \bf{u_k}^t \bf{u_i} )
\\
& = &
( \bf{a_n}^t \bf{u_i} ) - ( \bf{a_n}^t \bf{u_i} )
\\
& = &
0
\end{eqnarray}
\]
の関係が得られるので、\( \bf{a_n} \perp \bf{u_i} \ \rightarrow \ \bf{u_n} \perp \bf{u_i} \)となります。
従って、\( \bf{u_1},\cdots,\bf{u_n} \)は正規直交系であり、
\[
K\bf{a_1} + \cdots + K\bf{a_{n}} = K\bf{u_1} + \cdots + K\bf{u_{n}}
\]
を満たします。
******************** 証明おわり
2．2．グラム・シュミット法による数値計算
ここからは、グラム・シュミット法を用いたQR分解の計算手順について説明します。行列\( A \in R^{m \times n},Q,R \)を列ベクトル標記します。
\[
\begin{eqnarray}
A & = & (\bf{a_1}. \cdots, \bf{a_n}) \quad ( \bf{a_i} \in R^m )
\\
Q & = & (\bf{q_1}. \cdots, \bf{q_n}) \quad ( \bf{q_j} \in R^m )
\\
R & = & (\bf{r_1}. \cdots, \bf{r_n}) \quad ( \bf{r_k} \in R^n )
\end{eqnarray}
\]
このベクトル標記を用いて、行列\( A \)を1列ずつ順番に上三角化していきます。数値計算を行う際、グラム・シュミットの直交化法をそのまま適用するより、一部計算ロジックを修正した修正グラム・シュミット法を用いた方が計算安定性が増す、と言われています。 そこで、修正グラム・シュミット法の計算フローを以下に示します （なお、プログラムを記述する際、添数は0から始めるのが一般的ですので、それに基づき記述します）。
ところで、この計算フローではユニタリ行列Qは正方行列にはなりません。
理由は、列ベクトルの数分（n回）しか計算を行わないためです。
Qを正方行列にするためには、まずQの初期値としてm次単位行列を与え、計算完了後各列ベクトルが線形独立となるよう調整する必要があります。
