二分法
1.二分法
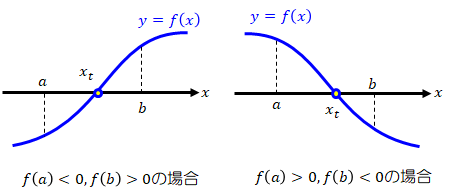
二分法は、方程式\( f(x)=0 \)の解を数値計算によって求める方法で、関数\( y=f(x) \)が持つ次の性質を利用しています。区間[a,b]で連続な関数\( y=f(x) \)が、\( f(a)f(b)<0 \)を満たすとき、その区間内に\( f(x)=0 \)を満たす点が存在します。
2.二分法の手順
関数\( y=f(x) \)が与えられたとき、ニュートン法を用いて\( f(x)=0 \)の解を求める手順を示します。 これは、関数\( y=f(x) \)と\( y=0 \)の二つの曲線の交点を求めることに他なりません。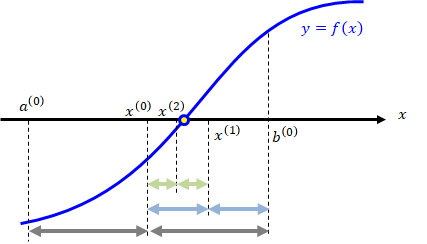
上図と一緒に各Stepの内容を確認してください。
Step1:
\( f(a^{(0)})f(b^{(0)})<0 \ \)を満たす\( a^{(0)}, b^{(0)} \ \)を決めます (\( a^{(0)} \lt b^{(0)} \ \))。Step2:
\( a^{(0)} \ \)と\( b^{(0)} \ \)の中間点\( x^{(0)} = (a^{(0)}+b^{(0)} \)/2 \)を求め、\( f(x^{(0)}) \)を算出します。Step3:
\( f(x^{(0)}) \)の絶対値が微小値\( \epsilon \)(収束判定値)より小さければ、\( x^{(0)} \ \)を\( f(x)=0 \)の近似解として処理を終了ます。
\[
| f(x^{(0)}) | < \epsilon
\]
上式を満たさない場合、次の場合分けに応じて処理を行います。
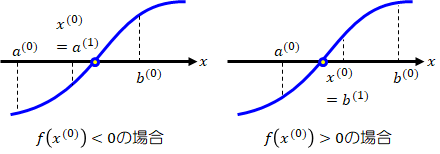
i)\( f(a)<0, f(b)>0 \)の場合
- \( f(x^{(0)}) < 0 \)の場合 → \( a^{(1)}=x^{(0)},b^{(1)}=b^{(0)} \)とします。
- \( f(x^{(0)}) > 0 \)の場合 → \( b^{(1)}=x^{(0)},a^{(1)}=a^{(0)} \)とします。
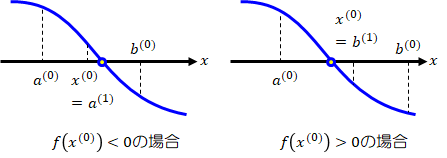
ii)\( f(a)>0, f(b)<0 \)の場合)
- \( f(x^{(0)}) < 0 \)の場合 → \( b^{(1)}=x^{(0)},a^{(1)}=a^{(0)} \)とします。
- \( f(x^{(0)}) > 0 \)の場合 → \( a^{(1)}=x^{(0)},b^{(1)}=b^{(0)} \)とします。
Step4:
Step3に基づき決めた\( a^{(1)} \ \)と\( b^{(1)} \ \)を用いてStep2、Step3の処理を繰り返します。 \( [a^{(0)} \,b^{(0)} \ ] \)で解が求まらなければ、\( [a^{(1)} \,b^{(2)} \ ] \)、\( [a^{(3)} \,b^{(3)} \ ] \cdots \)とStep2とStep3を繰り返し行います。3.二分法とニュートン法の比較
方程式\( f(x)=0 \)の解を求める方法として、二分法のほかにニュートン法があります。 ここではそれらのちゅほうの特徴について比較します。| 二分法 | ニュートン法 | |
|---|---|---|
| 収束の速さ | 遅い | 速い |
| 収束の確実性 | 高い | 高くない |
| 微分計算式 | 不要 | 必要 |
| 多変数関数への適用 | 難 | 易 |


