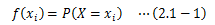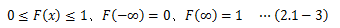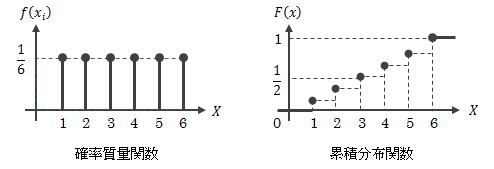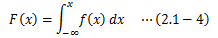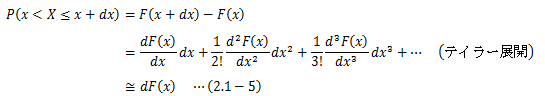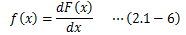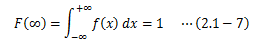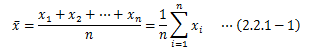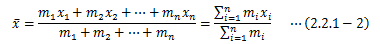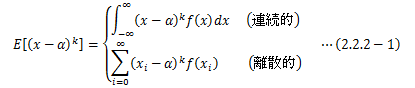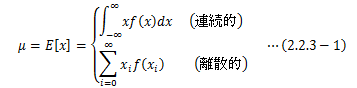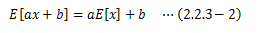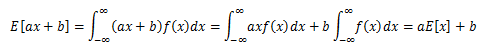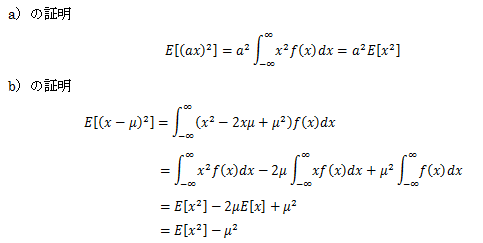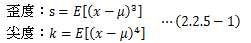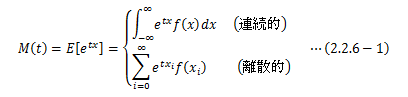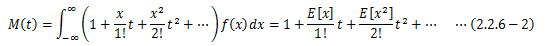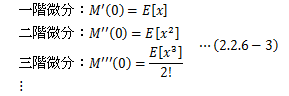確率・統計

2．確率分布

2．1．確率変数と分布関数

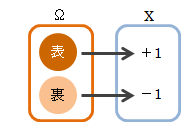
<標本空間Ω＝｛ω_i｜i＝1,2,…｝上の事象A_j（j＝1,2,…）に対し、何らかの実数x_jを割り当てます。このxjを選択する変数としてXを定義したとき、Xがx_jとなる確率は、事象A_jの出現確率で決まります。このように変数Xの値ごとに出現確率が決まるものを確率変数と呼びます。以上の内容から、確率変数は事象を実数に写す写像になります。

図2.1－1　確率変数の例

次に、確率変数Xがある特定の値x_iとなる確率P(X=x_i)を関数f(x_i)と置くとき、 f(xi)を確率関数あるいは確率質量関数と呼びます。

さらに、確率変数Xがx_i以下となる確率を示す関数F(x_i)を次式で定義できます。これを累積分布関数と呼びます。

累積分布関数は、確率の性質から次の条件を満たします。

ここで、確率質量関数と累積分布関数について、サイコロを例に表してみます（確率変数Xはサイコロの目と同じとします）。

図2.1－2　確率変数が離散的な場合

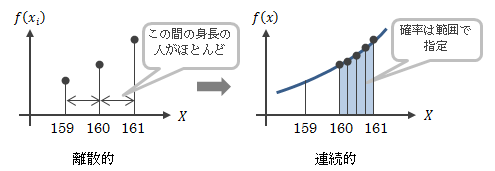
これまでは離散的な確率変数を対象としていましたが、現実には連続的な確率変数がほとんどです。例えば身長については、厳密に170cmの人はほぼゼロといってよいでしょう（170.0000…01cm≠170cm）。そのため、連続的な確率変数が扱えるよう、確率質量関数や累積分布関数を見直す必要があります。

図2.1－3　確率変数が連続的な場合

離散的な関数を連続的な関数に変える場合、微積分の概念を導入することになります。そこでまずは、累積分布関数（2.1－2）式を連続的な式に書き換えます。

これを用いれば、確率変数Xがxとx＋dx（微小量）の間に入る確率は、

となり、F(x)とf(x)の間には次の関係が成り立つことになります。

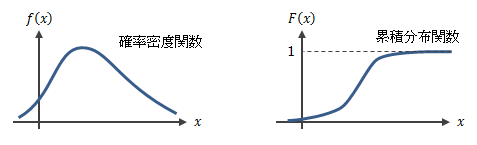
この関数f(x)を確率密度関数と呼びます。ただし確率密度関数は、それ自体が確率を表している訳ではなく、ある範囲の積分をとってはじめて確率を表すものになります。

図2.1－4　確率密度関数と累積分布関数

最後に、連続した確率変数の累積分布関数についても離散的なものと同様、－∞～＋∞の範囲で積分すると1になります。

2．2．モーメント

2．2．1．平均の概念

平均は確率分布を考えるとき、重要な役割を担います。そこでまずは、平均の概念について見ることにします。平均という言葉はなかなか抽象的で難しいところですが、辞書によると「いくつかの数や量の中間的な値」という風に述べられています（デジタル大辞泉より）。この中間的な値の1つとして、相加平均（算術平均）があります。これは、n個の数x₁、x₂、…、x_nがあるとき、その総和を個数nで割ったものとして定義されます。

これに対しx₁、x₂、…、x_nのそれぞれにある重み量m₁、m₂、…、m_n（＞0）を設け、次式で定められる量を加重相加平均といいます。

これは、物理で見る重心と全く同じものであり、またm₁＝m₂＝…＝m_nのとき相加平均と同じものになります。

2．2．2．モーメントの定義

モーメントは積率とも呼ばれ、確率分布の特徴を表す代表値としての意味を持ち、その定義は次のようなものです。 xを確率変数、αを基準となる定数としたとき、 xとαの距離のべき乗（x－α）^kと確率密度関数の積を確率変数の全範囲で積分したもので、次式で表せます。

特に基準αと次数kを明示的に言うとき、αまわりのk次モーメントと呼びます。基準値αは“0”（原点）や平均値を与えるのが一般的です。
モーメントの持つ意味は次数kによって異なり、k＝1～4次のモーメントを用いるのが一般的です。本章では特にk＝1、2次のモーメントについて見ることにします。

2．2．3．期待値（平均値）

α＝0の一次モーメントを期待値または平均値といい、次式で表せます。

この定義式に対し（2.2.1－2）式を照らし合わせると、確率密度関数f(x)を全範囲で積分（足し合わせ）すると1になることから、期待値は加重相加平均になります。その意味で、期待値は平均値とも言えることになります。期待値は、「ある偶然事象によって得られる量（確率変数）のうち最も見込まれる量」を意味しますが、その値とドンピシャで一致する確率変数が存在するとは限りません。例えば、1～10の整数が同じ確率で出現する際の期待値は5.5となることからもわかります。
期待値は演算上、次の定理が成り立ちます。

証明はこちら

証明 **************************************************

閉じる

2．2．4．分散

α＝平均値の二次モーメントを分散といい、次式で表せます。

分散は、各確率変数と平均値の差である偏差の二乗の平均値として定義され、「ある事象が持つデータの、平均値からの散らばり具合を表す量」という意味を持っています。偏差には正負の方向性があることから、偏差の平均をとると“0”になるのは明らかです。偏差平均が毎回“0”では何も評価しようがありません。この問題は、偏差を二乗することで解消されます^※ （ばらつきを平均からの“距離”と考えれば、二乗をとるのは妥当と考えられます）。

※：	ほかの方法、例えば絶対値をとる方法もありますが、最も簡単かつ扱いやすい方法で評価するのが合理的です。

分散は演算上、次の定理が成り立ちます。