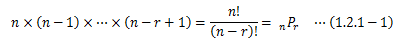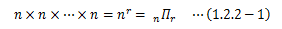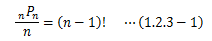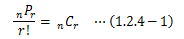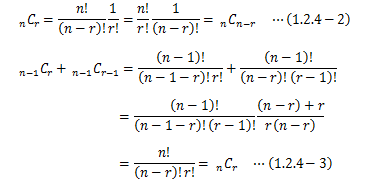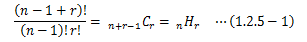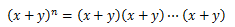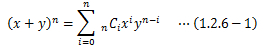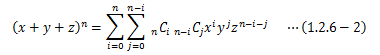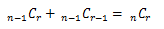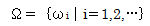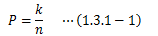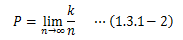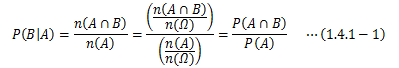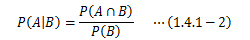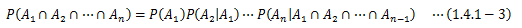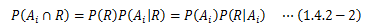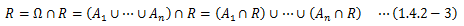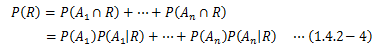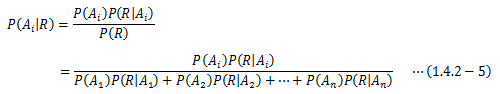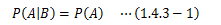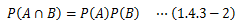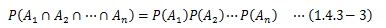確率・統計
1.確率の基礎概念
1.1.確率とは?
確率(Probability)とは、ある事象の発生割合を表すものです。 ここで出てくる事象とは何らかの行為によって得られた結果を意味し、 試行はその行為自体を表します。 例えば、サイコロを振る行為は試行であり、その結果偶数の目が出ることは事象に該当します。さて、不正のないサイコロを振ると、どの目も1/6の確率で出現することを私たちは経験的に知っています。 この当たり前の事実の裏には前提条件が存在しており、確率はその前提に基づき成り立っています。 この前提条件をきちんと把握していないと確率の誤用を生み、 最終的に「確率は役に立たない」といった間違った結論を導きだしてしまいます。 そこで本節では、前提条件を含めた確率の成り立ちについて、 簡単なコイントスの試行例を挙げながら迫ってみたいと思います。
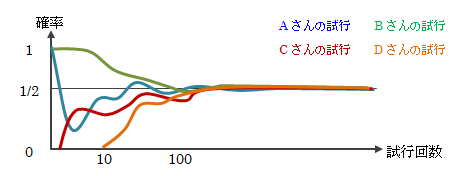
完全に対称なコインで1回だけ試行する場合、表と裏のどちらが出るか?を予測するのは本来不可能です。 それは、コイントスを行うときの力の入れ具合や、その後のコインの挙動、 落ちた場所の状態等を完全に把握することは不可能なためです(もしできるなら力学的に予測可能です)。 このような不確かな事象を偶然事象(ランダム事象)と呼びます。 この試行を繰り返す場合を考えます。 この時、それぞれの試行が関連性を持たない、つまり独立であることを前提とします。 この場合、前の結果に影響されず、後の結果は各試行独自に決まります。 仮に10回程度の試行なら、コインの表が出る割合は予測困難ですが、 100回、1,000回、・・・、極限まで増やすと、その確率は1/2になることを私たちは経験的に知っています。
図1.1-1 コイントスで表が出る確率(例)
このように独立試行の回数を極限まで増やせば、不確かな事象に何らかの規則性が現れてきます。 言い方を変えれば、偶然性で支配されていたはずの事象が、 気が付いたらいつの間にか必然性(規則性)に支配されていたことになります。 これを大数の法則と呼びます。
実はこのとき、確率の捉え方が2通りあることに気づきます。 1つ目は、コインには表と裏の2つしかなく、さらには不正がないため、 どちらかが必然的に現れるのはおかしく同じ割合で出現するはずだ、と捉える方法です。 これを数学的確率と呼びます。 数学的確率は表と裏、合計2つの場合の数に対しどちらか1つの場合が等しい割合でランダムに出現する、 という「場合の数の比」で定義されます。 2つ目は、何度も繰り返し試行した結果、表と裏は同じ割合で出現する、という結果論で捉える方法です。 これを経験的確率と呼びます。 経験的確率は、大数の法則に基づき得られた事象の発生割合で定義されます。
以上の内容を踏まえ、確率を知る上で意識しておかなければならない重要なことは、以下の三点になります。
- ランダム事象であること
- 独立試行であること
- 大数の法則に基づくこと
1.2.場合の数
前節で見たように、確率は場合の数を求めることから始まります。 そこで本節では、さまざまな場合の数の求め方について見ていくことにします。1.2.1.順列
順列とは、異なるn個のものから任意にr個を選んだときの並べ方の数です。 1個目を選ぶときは、n個の中から1個を選ぶのでn通り、2個目を選ぶときはn-1通り、・・・、 r個目を選ぶときはn-(r-1)通りとなり、次のように計算します。1.2.2.重複順列
重複順列は、異なるn個のものから同じものを繰り返し選ぶことを許してr個を選んだ時の並べ方の数です。 このとき毎回n通りの選び方があるので、次のように計算します。この例としては、おみくじ選びが挙げられます。
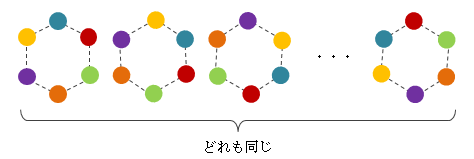
1.2.3.円順列
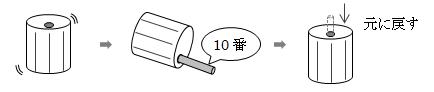
円順列とは、異なるn個のものを円形に並べたときの並べ方の数で、 特徴的なのは円形なので端がなく、全体を回転させると区別がつかないことにあります。 そのため、先頭の位置となるn箇所分の区別がつかないため、次のように計算します。図1.2.3-1 円環順列の例
1.2.4.組み合わせ
組み合わせは、異なるn個のものから順序を考慮せずにr個を選んだ組の数です。 これは並べ方の数r!を考慮しないことを意味しており、(1.2.1-1)式をr!で割れば求められます。なお、このnCrについては次の関係式が成り立ちます。
1.2.5.重複組み合わせ
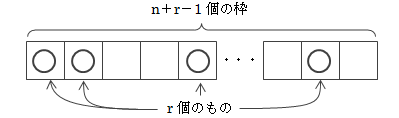
重複組み合わせは、 異なるn個のものから同じものを繰り返し選ぶことを許してr個を選んだ時の組の数です。 この場合、n個のものを区別するために、仕切りが(n-1)個存在すると考えます。ここで、繰り返しを許してr個のものを選び出すとき、下図の例のように、ものの違いがあるところに仕切りを入れてみます。
この図を白黒にしてみても、仕切りがあることから何色が何個あるかを識別できます。
これは結局のところ、下図のようにものと仕切りの合計n+r-1個の枠に、r個のものの入れ方の数を求めればよく、
次の計算で求められます。
1.2.6.多項定理
場合の数を応用すると、(x+y)nの展開式を簡単に導き出すことができます。 展開における最大の課題は、xiyn-i(i=0,1,2,…,n)の項の係数を求めることですが、この係数は、各(x+y)からxをi個選ぶ組み合わせの数nCiに等しくなります。
従って、(x+y)nの展開式は次のようになります。
この関係を二項定理と呼びます。 さらにこの関係を多項式に展開すると次の関係式が得られ、これを多項定理と呼びます。
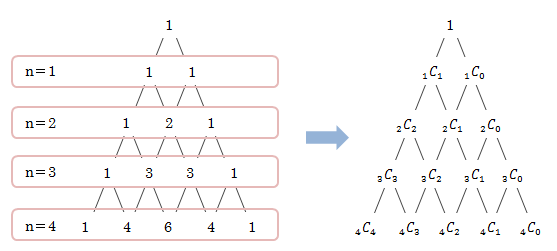
特に二項定理の各係数をうまく並べると、下図のようなパスカルの三角形と呼ばれる表現が可能になります。 これは、上の階層の二つの数を足し合わせたものが下の階層の値になっていることを表しています。
図1.2.6-1 パスカルの三角形
この関係から、(1.4.2-2)式が直ちに導きすことができます。
1.3.確率の性質
1.3.1.集合との関係
確率は、集合の概念と密接につながっています。 そこでまずは、集合の概念の中で確率に密接に結び付いたものの語彙について見ることにします。| 用語 | 定義 | 例 |
|---|---|---|
| 試行 | 同一条件のもと繰り返すことができる実験や観察のこと | サイコロの目の出方を調べる行為 |
| 事象 | 試行の結果 | 「1の目が出た」とか「偶数の目が出た」という結果 |
| 根源事象 | これ以上分割できない事象 | 「1の目が出た」~「6の目が出た」という事象 |
| 結合事象 | 二つ以上の根源事象を含むもの | 「偶数の目が出た」とか「5以上の目が出た」という事象 |
| 標本空間 | 根源事象をすべて集めた集合 |
サイコロ:{1,2,3,4,5,6} コイントス:{表,裏} |
以上の定義から、根源事象をωiとして標本空間Ωを表すと
であり、結合事象は任意に選ばれたωiを元とするΩの部分集合になります。 例えば、サイコロの目で事象Ajを考えれば次のようなものが挙げられます。
図1.3.1-1 標本空間と事象の例
以上の語彙を定義したことで、確率は次のように言い表すことができます。 標本空間に含まれるすべての根源事象の数をn、発生事象に含まれる根源事象の数をkとしたとき、 どの根源事象も同じ確からしさで生じるならば、 発生事象の数学的確率P (1.1節参照)は次式で表せます。
これに対し、どの根源事象も同じ確からしさで発生するという保証はなく、試行の回数をn、 その間の事象の発生回数をkとしたとき、経験的確率P (1.1節参照)は次式で表せます。
実際には試行を∞に行うことはできませんので、十分大きなnによって確率Pを求めることになります (その場合、その確率の信頼度というものを考慮しなければなりません)。
1.3.2.確率の性質
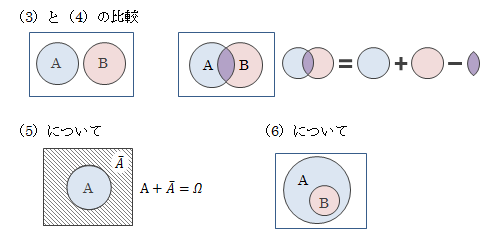
標本空間をΩ、複数の事象をA、Bとします。 このとき、確率には次の性質があります。図1.3.2-1 確率の性質を表すベン図
1.4.条件付き確率
1.4.1.条件付き確率
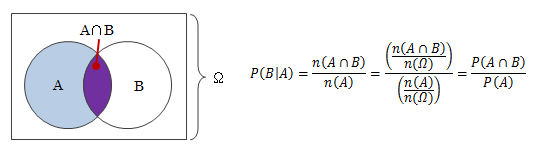
2つの事象A、Bがあり、Aが発生した条件下でBが発生する事象をB|Aと書くことにします。 このとき確率P(B|A)を条件付き確率といい、次式で求められます。これは以下のベン図をもとに考えるとわかりやすいと思います。 なお、事象A、Bおよび標本空間Ωの場合の数をn(A)、n(B)、n(Ω)で表します。
さて、(1.4.1-1)式は対称性を持つため、事象A|Bの確率は
で求められます。 また、事象が2つ以上ある場合は(1.4.1-1)式を繰り返し用いることで、次の関係式が得られます。
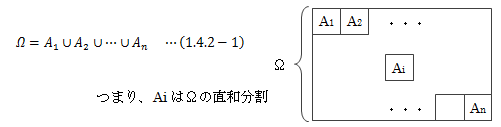
1.4.2.ベイズの定理
標本空間Ωと互いに排反な事象A1、A2、…、Anの間に次の関係が成り立つ場合を考えます。この条件下で、結果RがΩの中の1つの事象によって得られるとき、 事象Aiに起因する確率P(Ai|R)は次のようにして求められます。 (1.4.1-1)、(1.4.1-2)式より、
となります。ここで、結果Rと標本空間Sの間に成り立つ関係
と、各事象Aiが排反であることによって、次式が得られます。
これを(1.4.2-2)式に代入し変形すると、
が得られ、これをベイズの定理と呼びます。
1.4.3.ベルヌーイ試行
A、Bそれぞれの事象が互いに影響を及ぼしあわない、 つまりA、Bが独立な事象のとき、Aの発生確率はBの確率に依らないので、次式が成り立ちます。これを(1.4.1-2)式に代入すれば、独立事象A、Bに対し、BのもとAが起きる、 あるいはAのもとBが起きる確率は、互いの発生確率の積で求められることがわかります。
これを(1.4.1-3)式に適用すれば、
となることがわかります。 このよう試行を独立試行(ベルヌーイ試行)と呼びます。