数の概念
4.特殊な数
4.1.ゼロ(零)“0”
“0”とは「何もない」ことを表します。 この「何もない」という意味から、次の用途に用いられています。<量や大きさがないことを表す“0”>
何にもないことを表す0になります。
<数字の桁を表すための“0”>
105や0.0301などで用いる0のことで、ある桁に数字がない=空位を表します。
<座標原点/基準としての“0”>
正負の判別基準となる0のことで、0を境に大きい数字を正“+”、小さい数字を負“-”と呼びます。
0は四則演算に対しても強い特徴を示します。
(1)4.1.1.“0”の足し算・掛け算
0=0+0=0+0+0=0+0+・・・
上式が成り立つ数は“0”だけです。
ここで0の性質について見ていきます。 任意の数aについて、0は次の関係を有します。
- a+0=a
- a-0=a
- a×0=0
まずは(1)、(2)について、“a+0≠a-0”を仮定すると、
a+0>a-0またはa+0<a-0
のどちらかが成り立ちます。a+0>a-0のとき、右辺を左辺に移項すると0+0>0になり、0>0が成立しなければなりません。
同様にa+0<a-0のとき、右辺を左辺に移項すると0+0<0になり、0<0が成立しなければなりません。
0=0ですから上記2つはどちらも矛盾します。 よって、a+0=a-0となります。
そこで右辺の0を左辺に移項すると、a+0+0=aとなり、0+0=0であることからa+0=aとなりますし、 この式の左辺の0を右辺に移項すればa=a-0となります。
次に(3)について、a×0は
a×0=a×(0+0)
⇔ a×0=a×0+a×0
と書き換えられます。 ここでa×0=bとおくと、上式はb=b+bになります。 ところで、この関係式が成立するのは“0”だけですのでb=0となります。 よって、a×0=0になります。
(2)“0”の割り算
b÷0=cと仮定します。 するとこの式は次のように書き換えることが出来ます。b÷0=c ⇔ b=c×0
もしb=3だとしたら3=c×0 となり、前項の“a×0=0”に矛盾します。 つまり、この計算ではcを満たす数は存在しない、ということになります。 これはb≠0のどんな数に対しても起こります。
次にb=0、つまり0÷0=cのときを見てみます。 このとき0=c×0となりますので、cは任意の値を解とすることが出来ます。 ただこれも結局のところ、解を一意に決めることが出来ない=不定であることを表しています。
まとめると、
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
b \div 0 = 解なし( b \neq 0 )
\\
0 \div 0 = 不定
\end{array}
\right.
\end{eqnarray}
\]
となり、b≠0にせよb=0にせよ、分母に0を持ってくることに意味はないことを表しています。
4.2.無限大“∞”
無限大は数ではありません。 無限大の定義は次のようなものです。「限りなく大きくなるという事実を表す記号」
この意味から言えば、無限大は数ではなく現象を表している、と捉えることが出来ます。 この意味を明確にするため、次の式を考えます。
\[ \displaystyle \lim_{n \to \infty } n = \infty \] この式は、左辺の値が無限大“∞”という値に収束することを表しているのではなく、 左辺の値が限りなく大きくなる=発散する、ということを表しています。
ここで、無限大の四則演算について見てみます。
(1)a÷∞=0
これは無限小を表していて、限りなく0に近づく=0に収束することを表しています。
(2)∞+a=∞
これは、∞という数とある数aとの和を表しているのではありません。それは∞が数ではないからです。
この式の意味は、∞に発散する数列とaに収束する数列の和がいくらか?ということです。
収束の条件は数列の有界性ですが、発散する項が含まれているため、∞+aは∞に発散することになります。
(3)∞-∞=不定
±∞に発散する数列は山のようにあります。
例えば次のような数列を考えます。
\[ 1,2,3,\cdots,n,\cdots \ \leftrightarrow \ a_n = n \] この数列anは∞に発散します。 この各項に1/nを追加した数列を次のようにとります。
\[ 1+\frac{1}{1},2+\frac{1}{2},3+\frac{1}{3},\cdots,n+\frac{1}{n},\cdots \ \leftrightarrow \ b_n = n+\frac{1}{n} \] この数列bnも∞に発散します。 これらの数列の差bn-anをとると、
\[ \frac{1}{1},\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots, \] となり、この数列は0に収束します。
また、新たな数列として次のようにものを考えます。
\[ 2,4,6,\cdots,2n,\cdots \ \leftrightarrow \ c_n = 2n \] この数列cnも∞に発散します。 ここで、cn-anを計算すると、
\[ 1,2,3,\cdots,n,\cdots \ \leftrightarrow \ a_n = n \] となり、この数列は∞に発散します。 逆にan-cnを計算すると-∞に発散します。
つまり、∞-∞は一意には決まらないことがわかります。
\[ 1,2,3,\cdots,n,\cdots \ \leftrightarrow \ a_n = n \] この数列anは∞に発散します。 この各項に1/nを追加した数列を次のようにとります。
\[ 1+\frac{1}{1},2+\frac{1}{2},3+\frac{1}{3},\cdots,n+\frac{1}{n},\cdots \ \leftrightarrow \ b_n = n+\frac{1}{n} \] この数列bnも∞に発散します。 これらの数列の差bn-anをとると、
\[ \frac{1}{1},\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots, \] となり、この数列は0に収束します。
また、新たな数列として次のようにものを考えます。
\[ 2,4,6,\cdots,2n,\cdots \ \leftrightarrow \ c_n = 2n \] この数列cnも∞に発散します。 ここで、cn-anを計算すると、
\[ 1,2,3,\cdots,n,\cdots \ \leftrightarrow \ a_n = n \] となり、この数列は∞に発散します。 逆にan-cnを計算すると-∞に発散します。
つまり、∞-∞は一意には決まらないことがわかります。
(4)∞×0=不定
(2)同様、数列の具体的な例を持って話を進めます。
ここで次のような3つの数列を考えます。
\[ 1,2,3,\cdots,n,\cdots \ \leftrightarrow \ a_n = n \] \[ \frac{1}{1},\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots \ \leftrightarrow \ b_n =\frac{1}{n} \] \[ \frac{1}{1^2},\frac{1}{2^2},\frac{1}{3^2},\cdots,\frac{1}{n^2},\cdots \ \leftrightarrow \ c_n =\frac{1}{n^2} \] まずはan×bnを計算すると、
\[ 1,1,1,\cdots,1,\cdots \ \leftrightarrow \] という数列が出来ます。これは1に収束しますので、∞×0=1となります。
次にan×cnを計算すると、
\[ \frac{1}{1},\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots \] という数列が出来ます。これは0に収束しますので、∞×0=0となります。
このように、数列の種類によって∞×0は一意に決まらないことがわかります。
\[ 1,2,3,\cdots,n,\cdots \ \leftrightarrow \ a_n = n \] \[ \frac{1}{1},\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots \ \leftrightarrow \ b_n =\frac{1}{n} \] \[ \frac{1}{1^2},\frac{1}{2^2},\frac{1}{3^2},\cdots,\frac{1}{n^2},\cdots \ \leftrightarrow \ c_n =\frac{1}{n^2} \] まずはan×bnを計算すると、
\[ 1,1,1,\cdots,1,\cdots \ \leftrightarrow \] という数列が出来ます。これは1に収束しますので、∞×0=1となります。
次にan×cnを計算すると、
\[ \frac{1}{1},\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots \] という数列が出来ます。これは0に収束しますので、∞×0=0となります。
このように、数列の種類によって∞×0は一意に決まらないことがわかります。
4.3.円周率“\( \pi \)”
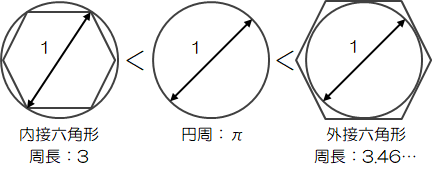
円周率とは、「円の周長÷直径」で求められる定数です。 円の面積を求める時にも必要となる、重要な値です。 この\( \pi \)は、小学生のときに3.14(ゆとり教育世代は3)として習いました。 ただし、実際は小数点2桁で終わりではなく、\( \pi \)=3.141592・・・という風に 無限に続く無理数になります。 コンピュータ開発の世界では、この\( \pi \)の計算桁数を争うことでその性能を競いあっていました (今では1兆桁以上算出されているそうです)。さて、この円周率\( \pi \)はどのようにして求められているのでしょうか?(理論的に、ですよ)
直径1の円を3つ準備します。 一つは、その円に内接する正六角形を書きます(下図左端)。 もう一つには、その円に外接する正六角形を書きます(下図右端)。
それぞれの正六角形の周長を計算すると、つぎのようになります。
図4.3-1 円周率\( \pi \)の求め方
つまり、円周率πは3と3.46の間にあることがわかります。 次に、この正六角形を正十二角形に変えて計算すると、 円周率は3.105・・・<\( \pi \)<3.215・・・となることがわかります。 このように直径1の円に内接する多角形と外接する多角形の周長を求めて、 それらの間に\( \pi \)が存在する、として計算していくことで、\( \pi \)の値を近似的に求めることができます (これをアルキメデスの方法と呼びます)。 この多角形の頂点数を無限に増やすことができれば、\( \pi \)の値を正確に求めることができる、と考えられますが、 現実的には不可能です。
4.4.自然対数“e”
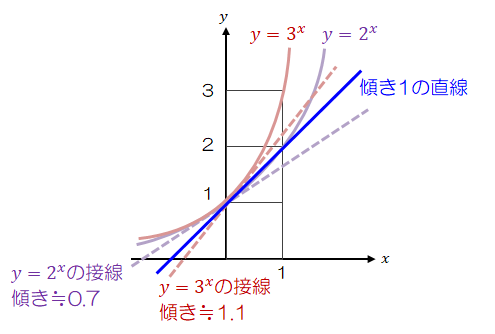
自然対数eは指数関数(XY)や対数関数(logX)を習う時に出てきます。 e=2.718281828459・・・という風に、π同様無限に続く無理数です。さて、自然対数eが2と3の間にあることが意味するところは次のような理由からです。 二つの関数y=2x、y=3xをそれぞれグラフに描きます。
図4.4-1 自然対数eの位置づけ
上図のとおり、x=0でy=2x、y=3xの接線を引くと、それぞれ傾きが0.7と1.1程度になります。 傾き1の直線はその間にあることがわかります。 そこで、y=exとした時に、x=0の接線の傾きが1となるような数字があるはず、として自然対数eが求められました。 この自然対数eには重要な特殊性を持っています。 特に接線の傾きが1となることから、微分積分の領域において威力を発揮します。