3．数の種類

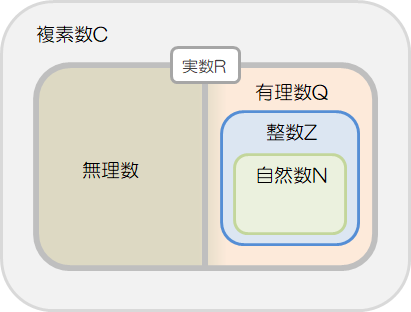
数は以下の6種類に大別されます。

自然数、整数、有理数、無理数、実数、複素数

3 ．1．自然数（Natural Numbe　集合：N）

下図のように、1、2、3・・・といった個数を表したり、順位を表す数字のことを言います。 数の起源と考えられています。 自然数の最小単位は“1”です。

図3.1－1　自然数を表す数直線

3．2．整数（Integral Number　集合：Z）

自然数は1より大きな数字でしたが、整数は、0やマイナス（-）も含みます。 整数の最小単位は、自然数同様“1”になります。

図3.2－1　整数を表す数直線

3．3．有理数（Rational Number　集合：Q）

有理数とは、以下のように定義されています。

2つの整数\(m , n \)によって \( \displaystyle \frac{n}{m} \)で表せる数（\(m \neq 0 \)））

つまり、分子、分母ともに整数にできる数、ということです。 ちなみに、自然数、整数とも有理数に含まれます（\( m = 1 \)のときの数）。

3．4．無理数（Irrational Number）

無理数は、有理数ではない数（実際は実数）、として定義されています。 例えば、自然対数e=2.718281…、円周率\( \pi = 3.141526… \)、\( \sqrt{2} =1.41421356… \)などがあります。 無理数であることを示すためには、“有理数ではない”という証明が必要になります。
例として、ここでは\( \sqrt{2} \)が無理数であることを証明します。 今、a、b、cの3つの整数が以下の関係を持つものとします。

（ただし、aとbの間に公約数はないものとする）

つまり“cは有理数である”と仮定しています。 すると、c²=2となりますので、上式を両辺二乗すると2b²=a²となります。 この場合、aは偶数になりますので、a=2sとおきます。 すると、2b²=4d² ⇔ b2=d²　となり、bも偶数になります。 この結果、a、bとも偶数になり、これは前提のa、b間に公約数がない、とする条件に矛盾します。 よって、\( \sqrt{2} \)は無理数である、と言えます。

3．5．実数（Real Number　集合：R）

実数とは、下図の矢印線上にあるすべての数を総括したものです。 つまり（1）自然数～（6）無理数のすべてを含みます。

図3.5-1　実数を表す数直線

3．6 ．複素数（Complex Number　集合：C）

複素数は虚数を含む数で、以下のように定義されています。

（a、bは実数）

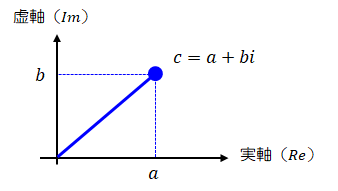
この表現からわかるように、複素数は実数を包括しています（b＝0）。 上記の実数部分（実部）a、虚数部分（虚部）bを以下のように表します。 実数が数直線上で表せるのに対して、複素数は横軸を実部、縦軸を虚部とする平面で表せます。

図3.6-1　複素数を表す平面

複素数を表す平面を、複素平面またはガウス平面と呼びます。 複素数の必要性については2.5項虚数を参照ください。
最後に自然数～複素数の数の関係は以下のようになります。

図3.6-2　数の種類に対する集合図

参考文献

関連ページ