公差の考え方
2.累積公差
2.1.公差の積み上げ方法
1章では部品単体の公差設定について見てきました。実際の工業製品は複数部品の組み合わせで構成されるのが一般的ですから、複数部品の公差が積み上がったうえで機能・性能要求を満足しなければなりません。 機能・性能観点で設計する際、まずはノミナル値(称呼寸法)をベースに検討・設計計算を行います。従って、公差幅が広くなるほど想定から外れるリスクが上がるため、設計者の心情として極力公差の幅は狭めたいのが本音です。 しかしながら、必要以上に公差幅を詰めると今度はコストがかかりすぎたり、最悪の場合そのような精度では作れない、といった結果を招きます。
そこで本章では、公差の積み上げ方法とその妥当性について見ていくこととします。
ちなみに、積み上げ公差は累積公差や集積公差等で呼ばれるのが一般的です。
ここでは話を簡単にするため、次のような事例をもとに公差の積み上げ方法について考えていきます。
事例:2つの棒をつなげたとき、つなげた棒全体の長さにどのような公差を与えるのが適切か?
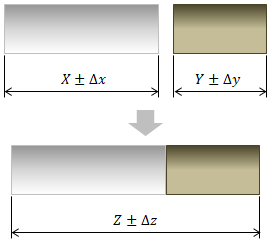
図2.1-1 公差積み上げの例
公差の積み上げ方法として行われているのは、主に次の二通りになります。- 単純積算(L.S.=Linear Sum)
- 二乗和 (R.S.S.=Root Sum Square)
- 積み上げ公差の大きさ
- 積み上げ公差を満足する確率
\[
( \Delta x + \Delta y ) > \sqrt { \Delta x^2 + \Delta y^2 } \quad ( \because \Delta x > 0 , \Delta y > 0 )
\]
従って、部品を組み合わせれば組み合わせるほど単純積算では公差が積み上がり、設計想定からの逸脱幅が大きくなることから、好ましくありません。
次に、公差が持つの確率の意味について見ていきます。
仮に公差が\( \sigma \)(標準偏差)管理であれば、\( \Delta x=\sigma_{x} \)、\( \Delta y=\sigma_{y} \)になります。 つまり、それぞれの棒の長さが公差を逸脱する確率は、ともに32%になります。
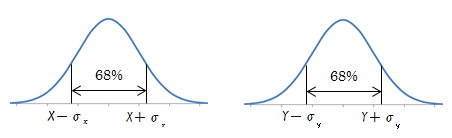
図2.1-2 公差設定範囲の確率
ここで、これらの棒をつなげたときに生じる積み上げ公差の逸脱確率を求めます。はじめに、単純積算(L.S.)により公差\( Δz_{L.S.} \)を逸脱する確率は、0.322×100=10.24%になります。 仮に棒の本数をn本とした場合、公差\( Δz_{L.S.} \)を逸脱する確率は(0.32n×100)となり、本数が増えれば増えるほど公差を逸脱する確率が飛躍的に減少することがわかります(その分公差幅も飛躍的に広くなります)。
次に、二乗和(R.S.S.)により公差\( Δz_{R.S.S.} \)を逸脱する確率は、誤差伝播の法則により32%のままになります(これについては2.2節で説明します)。 二乗和では、仮に棒の本数をn本にしても確率はそのまま32%を維持します。
このように、公差を\( \sigma \)管理とした場合の公差逸脱確率の関係は、
単純積算(10.24%)<二乗和(32%)
となり、単純積算と二乗和では確率的に大きな違いが生まれます。従って、“公差幅の大小”、“公差逸脱リスクの大小”を考慮して公差設定方法を選択する必要があります。
これらの使い分けは、製品不具合のリスクの度合いに基づくことが多いようです。
重篤な発生リスクが公差によって生じる場合は、コストを掛けてでも公差幅を詰める努力が必要です。 それに対し、ばらついてもあまり問題が生じないにもかかわらず、むやみな公差を与えてしまうと、無駄にコストがかかってしまいます。 以上の内容をもとに設計者は「公差逸脱の確率をコントロールしながら、品質と経済性の両立=製品最適化設計」を行っていく必要があります。
2.2.二乗和の根拠(誤差伝播の証明)
前節で個々の部品の公差を\( \sigma \)管理としたとき、二乗和による累積公差も\( \sigma \)管理となること、その理由は誤差伝播の法則に従うため、と述べました。 そこで、本項では二乗和の根拠となる“誤差伝播の法則”について見ていきます。なお、この誤差伝播の法則は\( \sigma \)管理だけでなく、\( 3 \sigma \)管理や\( 4.56 \sigma \)管理など、任意の係数(正の実数)でも成り立ちますし、2変数でなくても成り立ちます。
本節でも図2.1-1の例を用いて、公差\( \sigma \)管理、2変数における誤差伝播の法則を証明します。
はじめに計算を簡単にするため、図2.2-1のように棒の基準値( \(X,Y\) )が0となるように変数変換を行います。 この変数変換では基準値のみが変わり、分布の形は変わりません(単純な平行移動)。
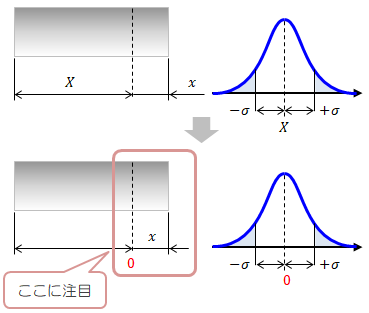
図2.2-1 棒の長さと分布曲線のの変数変換
棒1、棒2がそれぞれ長さ\(x\)、\(y\)となる確率は、正規分布関数\(f(x)\)によって次のように表せます。| 棒1が長さ\( x \)になる確率 | : | \( f(x) = \frac {1}{\sqrt{2 \pi} \sigma_x} \exp { ( -\frac {x^2} { 2 \sigma_x^2 } )} \) |
| 棒2が長さ\( y \)になる確率 | : | \( f(y) = \frac {1}{\sqrt{2 \pi} \sigma_y} \exp { ( -\frac {y^2} { 2 \sigma_y^2 } )} \) |
\[ f(x,y) = f(x) f(y) = \frac {1}{ 2 \pi \sigma_x \sigma_y } \exp \left( - \frac {1}{2} ( \frac {x^2} { \sigma_x^2 } + \frac {y^2} { \sigma_y^2 } ) \right) \]
今証明したいのは、棒全体の長さ\( (x+y) \)を確率変数として正規分布が作れるかどうか?ということです。そこでeの乗数(expの()内)に\( (x+y) \)を作って変形してみると次のようになります。
\[
\frac {x^2} { \sigma_x^2 } + \frac {y^2} { \sigma_y^2 }
= \frac { (x + y)^2} { \sigma_x^2 + \sigma_y^2 } + \frac {(\sigma_y^2 x - \sigma_x^2 y )^2} { \sigma_x^2 \sigma_y^2 (\sigma_x^2 + \sigma_y^2) }
= \frac {w^2} { \sigma_w^2 } + \frac {z^2} { \sigma_z^2 }
\]
ただし、
\[ \begin{eqnarray}
\left\{
\begin{array}{l}
w = x + y \\
z = \sigma_y^2 x - \sigma_x^2 y
\end{array}
\right.
\quad
\left\{
\begin{array}{l}
\sigma_w^2 = \sigma_x^2 + \sigma_y^2 \\
\sigma_z^2 = \sigma_x^2 \sigma_y^2 (\sigma_x^2 + \sigma_y^2)
\end{array}
\right.
\end{eqnarray} \]
これを\( f(x,y) \)に代入すると、次のように\(w,z\)の関数として書き換えられます。
変数\(w(=x+y)\)が棒全体の長さを表す確率変数であるため、今後は変数\(w\)に着目します。
\[ \begin{eqnarray}
f(x,y) &=& \frac {1}{ 2 \pi \sigma_x \sigma_y } \exp \left( - \frac {1}{2} ( \frac {x^2} { \sigma_x^2 } + \frac {y^2} { \sigma_y^2 } ) \right) \\
&=& \frac {1}{ 2 \pi \sigma_x \sigma_y } \exp \left( -\frac {w^2} { 2 \sigma_w^2 } \right) \exp \left( - \frac {z^2} { 2 \sigma_z^2 } \right) \\
&=& f(w,z)
\end{eqnarray} \]
ここで、全事象の発生確率は次式で表せるように、必ず1であることに注意します。
\[ \displaystyle \int_{ -\infty }^{ +\infty } \displaystyle \int_{ -\infty }^{ +\infty } f(x,y) dx dy = 1 \]
今、\((x,y)\)から\((w,z)\)に変数変換していることから、\(f(w,z)\)も上式を満たすことになりますが、変数変換の条件を追記しなければなりません。
2積分変数の変換ゆえヤコビアンを適用します。
\[ \begin{eqnarray}
dw dz &=& \begin{vmatrix} 1 & 1 \\ \sigma_y^2 & -\sigma_x^2 \end{vmatrix} dx dy \\[ 15pt ]
&=& ( \sigma_x^2 + \sigma_y^2 ) dx dy
\end{eqnarray} \]
\[
\therefore \displaystyle \int_{ -\infty }^{ +\infty } \displaystyle \int_{ -\infty }^{ +\infty } f(w,z) \frac { dw dz } { ( \sigma_x^2 + \sigma_y^2 ) } = 1
\]
このとき変数\(w,z\)が互いに独立であれば、今着目している棒全体の長さ\(w\)とは無関係な\(z\)について\( - { \infty } \lt z \lt + { \infty } \)で積分すれば\(z\)を含む項は定数化され、\( f(w,z) \)を\( f(w) \)の関数に書き換えることができます。
実際\(w\)と\(z\)はともに\(x\)と\(y\)の関数ですが、\(w\)を固定したところで\(z\)を決めることはできません。従って、\(w\)と\(z\)も独立になります。\[
\begin{eqnarray}
& & f(w - \delta w \leqq w \lt w + \delta w) \\[ 15pt ]
&=& \displaystyle \int_{ w - \delta w }^{ w + \delta w }
\displaystyle \int_{ -\infty }^{ +\infty }
f(w,z) \frac { dw dz } { ( \sigma_x^2 + \sigma_y^2 ) } \\[ 10pt ]
&=& \displaystyle \int_{ w - \delta w }^{ w + \delta w }
\displaystyle \int_{ -\infty }^{ +\infty }
\frac {1}{ 2 \pi \sigma_x \sigma_y }
\exp \left( -\frac {w^2} { 2 \sigma_w^2 } \right)
\exp \left( - \frac {z^2} { 2 \sigma_z^2 } \right)
\frac { dw dz } { ( \sigma_x^2 + \sigma_y^2 ) } \\[ 10pt ]
&=& \frac {1}{ 2 \pi \sigma_x \sigma_y ( \sigma_x^2 + \sigma_y^2 ) \hspace{ 10pt }}
\displaystyle \int_{ -\infty }^{ +\infty } \exp \left( - \frac {z^2} { 2 \sigma_z^2 } \right) dz
\displaystyle \int_{ w - \delta w }^{ w + \delta w } \exp \left( - \frac {w^2} { 2 \sigma_w^2 } \right) dw \\[ 10pt ]
&=& \frac { \sqrt { 2 \pi } \sigma_x \sigma_y \sqrt { \sigma_x^2 + \sigma_y^2 } \hspace{ 10pt }}{ 2 \pi \sigma_x \sigma_y ( \sigma_x^2 + \sigma_y^2 ) }
\displaystyle \int_{ w - \delta w }^{ w + \delta w } \exp \left( - \frac {w^2} { 2 \sigma_w^2 } \right) dw \\[ 10pt ]
\end{eqnarray}
\]
最後の変形は、次の関係式を用いた結果です。\[
\begin{eqnarray}
\begin{array}{l}
\displaystyle \int_{ -\infty }^{ +\infty } \exp \left( - \frac {z^2} { 2 \sigma_z^2 } \right) dz
= \displaystyle \int_{ -\infty }^{ +\infty } \exp \left( - \frac {z'^2} { 2 } \right) \sigma_z dz'
= \sqrt { 2 \pi } \sigma_z \\[ 10pt ]
\sigma_z = \sigma_x \sigma_y \sqrt { \sigma_x^2 + \sigma_y^2 }
\end{array}
\end{eqnarray}
\]
ここで、\( \delta w \rightarrow 0 \)の極限をとると関数\( f(w) \)が得られます。\[
f(w) = \frac { 1 } { \sqrt { 2 \pi } \sigma_w } \exp \left( - \frac {w^2} { 2 \sigma_w^2 } \right)
\]
関数\( f(w) \)は、変数\(w\)、基準値0、標準偏差\(\sigma_{w}\)とする正規分布を表しています。
| 棒全体の長さ | : | \( w = x + y \) |
| 棒全体の長さばらつき | : | \( \sigma_w = \sqrt { \sigma_x^2 + \sigma_y^2 } \) |
またこの関係、つまり誤差伝播は確率変数を増やしても成り立ちます(証明は厳密ではなく、かなり簡略化します)。
\[ \begin{eqnarray}
f(u_1, u_2, \cdots , u_n) &=& f(u_1) f(u_2) \cdots f(u_n) \\
&=& f(u_1 +u_2) \cdots f(u_{ n-1 } + u_n) \\
&=& \cdots \\
&=& f(u_1 + u_2 + \cdots + u_n) \\
&\propto& \exp { \left( - \frac { ( u_1 + u_2 + \cdots + u_n)^2 \hspace{ 20pt } } {2 ( \sigma_{u1}^2 + \sigma_{u2}^2 + \cdots \sigma_{un}^2 ) } \right) }
\end{eqnarray} \]
\[ \therefore \sigma_w = \sqrt { \sigma_{u1}^2 + \sigma_{u2}^2 + \cdots + \sigma_{un}^2 } \]
この式を分散の加法性と呼びます。次に、\(\sigma\)の係数となる任意の正の実数\( \alpha \)に対する確率の伝播について見ていきます。 それぞれの棒の長さを\( \alpha \sigma\)管理としたとき、棒1、棒2の公差は
| 棒1の公差 | : | \( \Delta x = \alpha \sigma_x \) |
| 棒2の公差 | : | \( \Delta y = \alpha \sigma_y \) |
\[
\begin{eqnarray}
\Delta z &=& \alpha \sigma_w \\
&=& \alpha \sqrt { \sigma_x^2 + \sigma_y^2 } \\
&=& \sqrt { ( \alpha \sigma_x )^2 + ( \alpha \sigma_y )^2 } \\
&=& \sqrt { \Delta x^2 + \Delta y^2 } \\
\end{eqnarray}
\]
これは結局のところ二乗和の計算そのものです。
つまり二乗和で公差設定する場合、個々の公差もそれを集積した公差も\( \alpha \sigma\)で管理されることになります。以上で誤差伝播の証明は終わりです。


