gijyutsu-keisan.com

1．ラプラス変換とは？

ラプラス変換とは、非常に大雑把に言えば「常微分方程式を解くために行う変数変換」のことです。 この変換のメリットは、微分方程式を解く際に出てくる微積分の複雑な計算を、簡単な代数演算に書き換えることができることにあります。
微分方程式を解く手順としては、次のようになります。
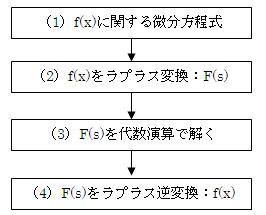ラプラス変換による微分方程式の解き方 さて、工学においてラプラス変換を用いる主なケースとしては次のようなものが挙げられます。
  • 電気や機械などの振動現象や過渡現象を数学的に求める場合
  • 制御系システムの数学的記述（伝達関数）

など

2．ラプラス変換の定義

ラプラス変換は次のように定義されます。

x＞0で定義される関数f(x)に対し、
\[ F(s) = L \{ f(x) \} = \int_{0}^{\infty} f(x) e^{-sx} \ dx \]

(sは複素数)


つまり、変数xで定義される関数f(x)を、変数sとする関数F(s)に変換することを表します。 ラプラス変換F(s)によってf(x)に関する微分方程式を解くことから、F(s)→f(x)に変換出来なければなりません。 この変換をラプラス逆変換といい、次のように定義されます。
\[ f(x) = L^{-1} \{ F(s) \} = \int_{a-i \infty}^{a + \infty} F(s) e^{sx} \ ds \]

(a > 0)


ちなみにラプラス変換とは、関数f(x)に関数e－ax（a＞0）を掛け、それをフーリエ変換たものです。
実際にラプラス変換を用いるときは、このような積分計算をいちいち行う必要はなく、代表的な関数についてラプラス変換表が準備されています。 この表をもとに微分方程式を書き換えていくことになります。 ラプラス変換表については、次項表3－1に示します。

3．ラプラス変換の性質

x＞0で定義される関数f(x)、g(x)に対し、ラプラス変換の演算について次のような性質が成り立ちます。
(1) \( L \{ f(x)+g(x) \} = F(s)+G(s) \)
(2) \( L \{ a f(x) \} = a F(s) \)
(3) \( L\{ \displaystyle \frac{d}{dx} f(x) \} = s F(s) \)
(4) \( L \left\{ \displaystyle \frac{d^n}{dx^n} f(x) \right\} = s^n F(s) - s^{n-1}f(0) - s^{n-2}f'(0) - \cdots -f^{(n-1)} \ (0) \)
(5) \( L \left\{ \displaystyle \int_{0}^{x} f(x) dx \right\} = \displaystyle\frac{1}{s}F(s) \)
(6) \( L \{ f(x) g(x) \} = F(s)G(s) \)
また、前述した各種関数のラプラス変換表を以下に示します。
表3－1　ラプラス変換表
\( f(x) \) \( F(s) \)
\[ \delta (x) \]
\[ 1 \]
\[ f(x)=1 \]
\[ \frac{1}{s} \]
\[ e^{-\alpha x} \]
\[ \frac{1}{s + \alpha} \]
\[ x \]
\[ \frac{1}{s^2} \]
\[ x^n e^{-\alpha x} \]
\[ \frac{n!}{ (s + \alpha)^(n+!) } \]
\[ \sin (\omega x) \]
\[ \frac{\omega}{s^2+\omega^2} \]
\[ \cos (\omega x) \]
\[ \frac{s}{s^2+\omega^2} \]
\[ e^{-\alpha x} \sin (\omega x) \]
\[ \frac{\omega}{(s+\alpha)^2+\omega^2} \]
\[ e^{-\alpha x} \cos (\omega x) \]
\[ \frac{s+\alpha}{(s+\alpha)^2+\omega^2} \]
\[ \frac{1}{\beta-\alpha}( e^{-\alpha x} - e^{- \beta x} \ ) \]
\[ \frac{1}{(s+\alpha)(s+\beta)} \]
\[ \frac{1}{\sqrt{1-\zeta^2}} e^{-\zeta \omega_n x} \sin \left( \omega_n \sqrt{1-\zeta^2 } x \right) \\ (\zeta \gt 1 )\]
\[ \frac{\omega_n}{s^2+ 2 \zeta \omega_n s + \omega_n^2} \]

4．ラプラス変換の例

ここでは、実際に一つの例を用いてラプラス変換による常微分方程式を解いて見ます。
\[ m \ddot{x} = -kx - c\dot{x} + F_o \sin (\omega t) \\ (\dot{x}(0)=0, x(0)=0) \tag{4-1} \]
（4－1）式をラプラス変換すると、
\[ \begin{eqnarray} m s^2 X(s) + c s X(s) + k X(s) & = & \frac{ \omega }{ s^2 + \omega^2} \\ \leftrightarrow X(s) & = & F_o \frac{\omega}{s^2 + \omega^2}\frac{1}{ms^2 + c s + k} \\ \leftrightarrow X(s) & = & \frac{F_o}{m} \frac{\omega}{s^2 + \omega^2}\frac{1}{ s^2 + \displaystyle \frac{c}{m} s + \frac{k}{m} } \end{eqnarray} \]
ここで、次のようにパラメータを設定すると、
\[ \omega_n = \sqrt{ \frac{k}{m}}, \zeta=\frac{c}{2\sqrt{mk}} \]
これを代入すれば、
\[ X(s) = \frac{F_o}{m} \frac{\omega}{s^2+\omega^2}\frac{1}{s^2 + 2 \zeta \omega_n s + \omega_n^2} \]
ここで、仮にm=1、c=2、k=1、F0=3、ω=1とすると、
\[ \begin{eqnarray} X(s) & = & 3 \frac{1}{s^2 + 1}\frac{1}{s^2 + 2s + 1} \\ \\ \leftrightarrow X(s) & = & \frac{3}{(s^2+1)(s+1)^2} \end{eqnarray} \]
ここで、部分分数展開により次のように書き換えます。
\[ X(s) = \frac{A}{(s+1)^2}+ \frac{B}{(s+1)}+ \frac{C}{(s+i)}+ \frac{D}{(s-i)} \]
そこでA、B、C、Dを求めると次のようになります。
\[ X(s) = \frac{3}{2} \left\{ \frac{1}{(s+1)^2}+ \frac{1}{(s+1)}- \frac{s}{(s^2+1)} \right \} \]
表3－1のラプラス変換表から上式をラプラス逆変換すると、
\[ x = \frac{3}{2} \left\{ t e^{-t} + e^{-t} - \cos (t) \right\} \]
となります。
以上のようにすれば、微積分の計算なしに代数演算のみで微分方程式を解くことが出来ます （部分分数展開に少しテクニックを必要とします）。
本章では、ラプラス変換の使用について見てきました。 ラプラス変換の数学的な内容については別途ページを設けて見ていきたいと思います。
▲