gijyutsu-keisan.com

回帰曲線（Excel関数）

Excel関数を用いることで、簡単に回帰曲線を求めることができます。 ここでは、直線近似（1次式）、多項式近似曲線、指数近似、累乗近似について見ていきます。
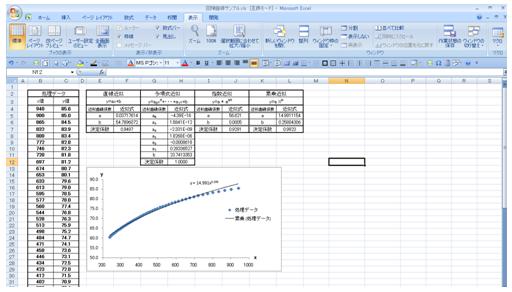
回帰曲線を求めるサンプルファイルを作成しましたので、こちらもご覧ください。
回帰曲線サンプル.xls
回帰曲線サンプル

1．直線近似

（x,y）の点群データから、直線である1次関数の近似直線を求めます。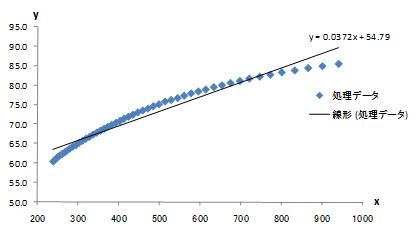
図1－1　近似直線　y=ax+b
図1－1　近似直線　y=ax+b
Excelで求める値は、係数であるaとy切片であるbになります。

（1）aを求める関数（セルに次の関数を入力）

  • =LINEST(y値のセル範囲、x値のセル範囲)
  • =INDEX(LINEST(y値のセル範囲、x値のセル範囲),1,1）

（2）bを求める関数（セルに次の関数を入力）

=INDEX(LINEST(y値のセル範囲、x値のセル範囲),1,2）
図1－2　近似直線の求め方
図1－2　近似直線の求め方
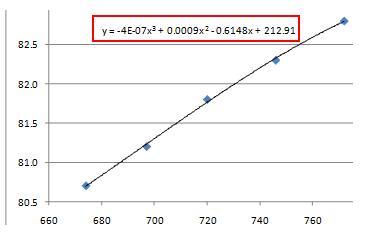
さて、求まった値が正しいことを確認するには、処理データの散布図を作成し、近似直線を求め、その式の係数とaを、定数とbを見比べます。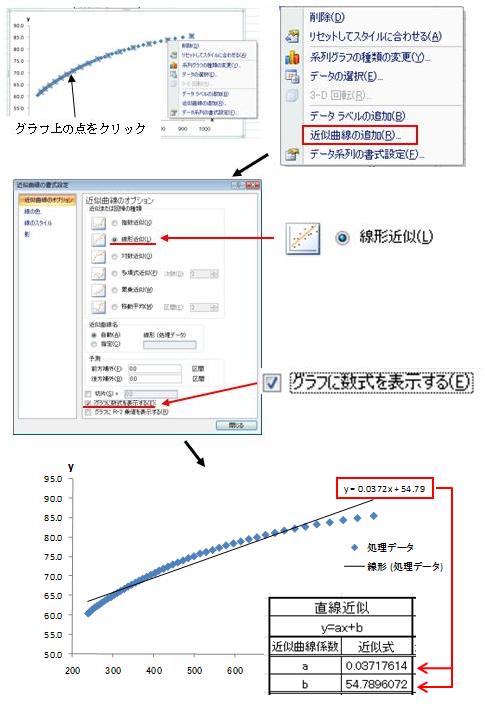
図1－3　グラフから求める近似直線
図1－3　グラフから求める近似直線
散布図グラフから近似直線式以外にも、近似多項式、指数近似式、累乗近似式を求めることができます。

2．多項式近似

（x,y）の点群データから、多項式による近似曲線を求めます。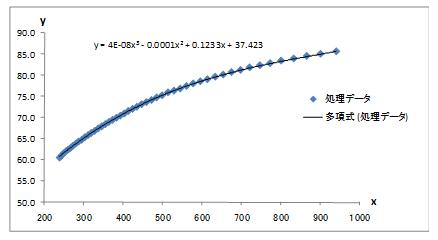
図2－1　近似多項式曲線　y=anxn+・・・+a1x+b
図2－1　近似多項式曲線　y=anxn+・・・+a1x+b

Excelで求める値は、n個の係数であるan・・・a1と、 定数であるbになります。

（1）an・・・a1を求める関数（セルに次の関数を入力）

=INDEX(LINEST(y値のセル範囲、x値のセル範囲^{n,n-1,・・・,1}),1,n）

（2）bを求める関数（セルに次の関数を入力）

=INDEX(LINEST(y値のセル範囲、x値のセル範囲^{n,n-1,・・・,1}),1,n+1）
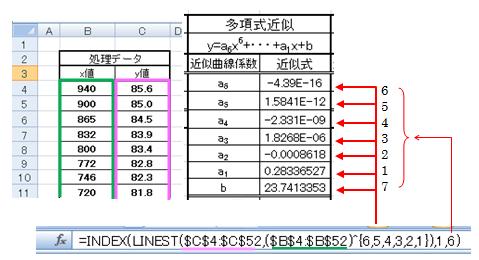
図2－2　多項式近似の求め方
図2－2　多項式近似の求め方
LINEST関数の特徴を掴むことによって、この関数の意味するところは明確になりますが、ここではその詳細な説明はExcelヘルプによるものとし、概略のみを説明します。
例としてx値が5つある場合の3次式近似曲線を求めてみます。
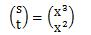多項式近似計算例 さて、この3次近似曲線を求めるには、新たに次のような変数を考えます。
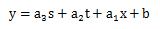多項式近似計算例 すると、
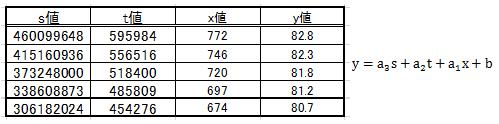多項式近似計算例 と表せます。 すると、多変量解析による回帰直線を求める式と同じ形になります。 そうすると、例の表は次のように書き換えれば、
多項式近似計算例 と表せます。

さて、LINEST関数は配列を返します。 Excelヘルプの記述に従えば、次の多変量の回帰直線
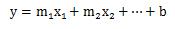
多項式近似計算例
のm1、m2、・・・、bを、LINEST関数の戻り値は配列として返すことになります。 では、具体的にExcelを用いて計算してみます。
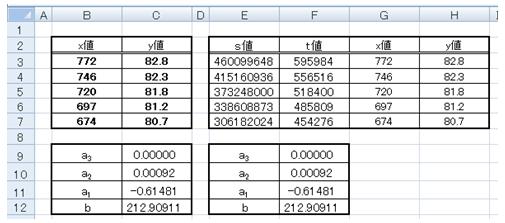
図2－3　LINEST関数の戻り値
図2－3　LINEST関数の戻り値
図2－3の左側は、今回紹介した関数によって算出したa3、a2、a1、bです。
B9セル（a3） =INDEX(LINEST(C3:C7,(B3:B7)^{3,2,1}),1,3)
B10セル（a2） =INDEX(LINEST(C3:C7,(B3:B7)^{3,2,1}),1,2)
B11セル（a1） =INDEX(LINEST(C3:C7,(B3:B7)^{3,2,1}),1,1)
B12セル（b） =INDEX(LINEST(C3:C7,(B3:B7)^{3,2,1}),1,4)
それに対し、図2－3の右側は、多変量でみた場合の回帰直線係数として算出した a3、a2、a1、bです。
E9セル（a3） ：=INDEX(LINEST(C3:C7, B3:G7),1,3)
E10セル（a2） ：=INDEX(LINEST(C3:C7, B3:G7),1,2)
E11セル（a1） ：=INDEX(LINEST(C3:C7, B3:G7),1,1)
E12セル（b） ：=INDEX(LINEST(C3:C7, B3:G7),1,4)
どちらも算出結果は同じになります。 確認のため、グラフから算出した多項式と見比べれば、計算結果が一致していることがわかります。
グラフで確認

3．指数近似

（x,y）の点群データから、指数関数による近似曲線を求めます。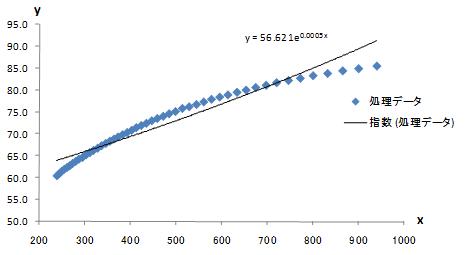
図3－1　指数近似曲線　y=a exp(bx)=a ebx
図3－1　指数近似曲線　y=a exp(bx)=a ebx
Excelで求める値は、指数関数の係数であるaとxの係数であるbになります。

（1）aを求める関数（セルに次の関数を入力）

  • =EXP(INTERCEPT(LN(y値のセル範囲)、x値のセル範囲)）
  • =EXP(INDEX(LINEST(LN(y値のセル範囲), x値のセル範囲),1,2))

（2）bを求める関数（セルに次の関数を入力）

  • =SLOPE(LN(y値のセル範囲)、x値のセル範囲)
  • =INDEX(LINEST(LN(y値のセル範囲), x値のセル範囲),1,1)
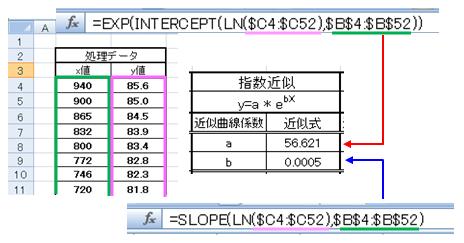
図3－2　指数近似の求め方
図3－2　指数近似の求め方
多項式近似のときと同様に、変数変換することで上式を導き出すことができます。 ところで、ここでは新しい関数“LN”、“INTERCEPT”、“SLOPE”が出てきました。 “LN”は数値を対数化する関数です。 その他の関数については以下の通りです。
  • INTERCEPT関数：回帰直線のy切片（y=ax+bの“b”）を算出
  • SLOPE関数：回帰直線の傾き（y=ax+bの“a”）を算出
LINEST関数を用いても同じことが計算できますが、これらの関数を用いることで記述が少し楽になります。

4．累乗近似

（x,y）の点群データから、累乗関数による近似曲線を求めます。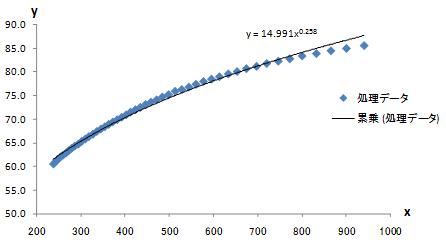
図4－1　累乗近似曲線　y=a xb
図4－1　累乗近似曲線　y=a xb
Excelで求める値は、累乗関数の係数であるaとxの乗数であるbになります。

（1）aを求める関数（セルに次の関数を入力）

  • =EXP(INTERCEPT(LN(y値のセル範囲)、LN(x値のセル範囲))）
  • =EXP(INDEX(LINEST(LN(y値のセル範囲)、LN(x値のセル範囲)),1,2))

（2）bを求める関数（セルに次の関数を入力）

  • =SLOPE(LN(y値のセル範囲)、LN(x値のセル範囲))
  • =INDEX(LINEST(LN(y値のセル範囲)、LN(x値のセル範囲)),1,1)
図4－2　累乗近似の求め方
図4－2　累乗近似の求め方
多項式近似や指数近似のときと同様に、変数変換することで上式を導き出すことができます。
▲