LU分解
3.クラウト法
クラウト法はLU分解の一つの手法で、上三角行列Uの対角成分をすべて1とおいて、Uの残りの成分と上三角行列Lを求めます。 これとは逆に、下三角行列Lの対角成分をすべて1として計算する手法をドゥーリトル法と呼びます。さて、クラウト法の実際の計算は次のようにして行います。
まず、Uの対角成分をすべて1とします。 次に非対角成分について、上三角行列Lなら下三角部分をすべて0、下三角行列Uなら上三角部分をすべて0とおけます。
\[
\begin{eqnarray}
\left\{
\begin{array}{1}
l_{ij}=0 \quad ( i \lt j)
\\
u_{ij}=0 \quad ( i \gt j)
\end{array}
\right.
\end{eqnarray}
\tag{3-1}
\]
これらが既知であることを利用して、次の計算式
\[
a_{ij}
=
\sum_{k=1}^s l_{ik} u_{kj}
\tag{3-2}
\]
から\( l_{ij}, u_{ij} \)を求めていきます。
\[
\begin{eqnarray}
\left \{
\begin{array}{1}
l_{ij}
=
a_{ij} - \displaystyle \sum_{k=1}^{j-1} l_{ik} u_{kj}
\quad ( i \geq j )
\\
u_{ij}
=
\frac{\displaystyle a_{ij} - \displaystyle \sum_{k=1}^{j-1} l_{ik} u_{kj}}{\displaystyle l_{ii}}
\quad ( i \lt j, l_{ii} \neq 0 )
\end{array}
\right.
\end{eqnarray}
\tag{3-3}
\]
このように、クラウト法は非常に簡単にLU分解できます。またクラウト法の別のメリットとして、メモリの節約が可能です。 これは、上三角行列の対角成分と、三角行列であることから非対角成分が0となる場所が決まっていることを利用して、上三角行列と下三角行列を一つの配列にまとめて格納できることにあります。
\[
\begin{pmatrix}
\txc{blue}{l_{11}} & \txc{red}{u_{12}} & \txc{red}{\cdots} & \txc{red}{u_{1n}}
\\
\txc{blue}{\vdots} & \txc{blue}{\ddots} & \txc{red}{\ddots} & \txc{red}{\vdots}
\\
\txc{blue}{\vdots} & & \txc{blue}{\ddots} & \txc{red}{u_{n-1,n}}
\\
\txc{blue}{l_{n1}} & \txc{blue}{\cdots} & \txc{blue}{\cdots} & \txc{blue}{l_{nn}}
\end{pmatrix}
\]
ところで、(3-3)式はクラウト法では\( l_{ii} \neq 0 \)を前提にしていますが、これは保証されません。
本来LU分解できる行列において\( l_{ii} = 0 \)となる場合は、ガウスの消去法2.2節で見た行ピボッティングを実行することで0割りを回避しLU分解可能になります(100%ではありあせんが)。
4.コレスキー分解
4.1.コレスキー分解とは?
行列Aが“正定値行列”のとき、Aは“コレスキー分解”できます。いきなりこの文章を見ても???となりますので、次のキーワードについてそれぞれ説明します。
(1)正定値行列
Aがn次正定値行列である、とは、次の条件を満足する行列のことです。
a)Aはエルミート行列
a)Aはエルミート行列
エルミート行列とは、Aの複素共役行列\( \overline{A} \)を転置したもの\( \overline{A^t} \)が、Aに等しい、という行列です。
\[
A^* = \overline{A^t} = A
\]
b)任意の\( \bf{x}, \bf{x} \neq \bf{o} \)に対して\( \bf{x^*}A\bf{x} \gt \bf{o} \)
(2)コレスキー分解
Lをn次下三角行列とします。
\( A = L L^* \)に分解できるとき、Aはコレスキー分解可能といいます。
\( L^* \)は上三角行列となるのでコレスキー分解はLU分解の一つと言えます。
4.2.コレスキー分解の証明
コレスキー分解のロジックに入る前に、まずはコレスキー分解の証明を行います。コレスキー分解は、この証明からわかるようにガウスの消去法の変形版と見ることができます。
証明******************************
Aは正定値行列とします。このとき、
\[
\begin{eqnarray}
&
\bf{e_1^*}A\bf{e_1}
& =
(1 \quad \bf{o}^t )
\begin{pmatrix}
a_{11} & \bf{a_{r1}} &
\\
\bf{a_{c1}} & A_{n-1,n-1} &
\end{pmatrix}
\begin{pmatrix}
1
\\
\bf{o}
\end{pmatrix}
\\
& & =
( a_{11} \quad \bf{a_{r1}} )
\begin{pmatrix}
1
\\
\bf{o}
\end{pmatrix}
=
a_{11} \gt 0
\end{eqnarray}
\tag{4.2-1}
\]
となります。
ここで、Aの第一行と第一列にガウスの消去法(変換行列をG1とします)を適用すると、ガウスの消去法の目的から次の形に変形できます。
\[
\begin{eqnarray}
&
G_1 A G_1^*
& =
\begin{pmatrix}
1 & \bf{o}^t &
\\
\bf{g_1} & I &
\end{pmatrix}
\begin{pmatrix}
a_{11} & \bf{a_{r1}} &
\\
\bf{a_{c1}} & A_{n-1,n-1} &
\end{pmatrix}
\begin{pmatrix}
1 & \bf{g_1}^* &
\\
\bf{o} & I &
\end{pmatrix}
\\
& & =
\begin{pmatrix}
a_{11} & \bf{o}^t &
\\
\bf{o} & A^{(1)}_{n-1,n-1} &
\end{pmatrix}
\end{eqnarray}
\tag{4.2-2}
\]
ここで次の計算を行います。
\[
\bf{x^*}G_1 A G_1^* \bf{x}
\tag{4.2-3}
\]
このとき\( \bf{y} = G_1^*\bf{x} \)とおくと、\( \bf{y}^* = \overline{ ( G_1^*\bf{x} )^t } = \bf{x}^t G_1 \)となるため、
\[
\bf{x^*}G_1 A G_1^* \bf{x}
=
\bf{y}^* A \bf{y}
\tag{4.2-4}
\]
と変形できます。
Aが正定値行列であることから、\( \bf{y}^* A \bf{y} \gt 0 \)を満たします。
さらに、(4.2-3)式を成分計算すれば
\[
\begin{eqnarray}
&
( \overline{y_1} \quad \bf{y}^* )
\begin{pmatrix}
a_{11} & \bf{a_{r1}} &
\\
\bf{a_{c1}} & A_{n-1,n-1} &
\end{pmatrix}
\begin{pmatrix}
{y_1}
\\
\bf{y}^*
\end{pmatrix}
\
& =
( \overline{y_1}a_{11} \quad \bf{y}^* A_{n-1,n-1} \ )
\begin{pmatrix}
{y_1}
\\
\bf{y}^*
\end{pmatrix}
\\
\\
& & =
\overline{y_1} y_1 a_{11} + \bf{y}^* A_{n-1,n-1} \bf{y}^*
\gt 0
\end{eqnarray}
\]
\( \overline{y_1} y_1 = |\bf{y}|^2 \gt 0, a_{11} \gt 0 \)であるから
\[
\bf{y}^* A \bf{y}
\gt
0
\tag{4.2-6}
\]
が得られます。
これを繰り返せばガウスの消去法に基づき
\[
A = LDL^*
\tag{4.2-7}
\]
が得られます(Dは対角行列)。Dの成分はdii>0であるから、コレスキー分解の形にするにはDの対角成分の平方根を成分とする対角行列D'をとって
\[
A = (LD')(D'L)^*=L'L'^*
\tag{4.2-8}
\]
とできます。今度はAがコレスキー分解可能としたとき、任意の\( \bf{x} \)に対し
\[
\bf{x}^*A\bf{x}
=
\bf{x}^* L L^* \bf{x}
=
\bf{y^*} \bf{y}
=
|\bf{y}^2|
\gt 0
\]
となります。
******************************証明おわり
4.3.修正コレスキー分解
ここからいよいよ数値計算の話に入ります。コレスキー分解する行列Aは正定値行列であることが条件でした。 この行列Aは、実行列でも複素行列でもどちらでも構いません。 そこで、本節では数値計算を目的としていることからAを実行列として話を進めます。 なおエルミート行列Aが実行列の場合、Aは対称行列となります。
\( \overline{ (\alpha + \beta i) } \ = \alpha - \beta i \) に対し、実行列なら\( \beta = 0 \)
この節では“修正”コレスキー分解を扱います。 “修正”とついている理由は以下の通りです。- コレスキー分解の計算に平方根を行う必要があり、計算安定性や精度にやや難があること
- 正定値でない対称行列の場合、平方根が虚数となるため扱いずらいこと
Aが実対称行列のとき、(4.2-7)式に基づき下三角行列Lと対角行列Dを用いて次のように分解できます。
\[
A=LDL^t
\tag{4.3-1}
\]
なお、下三角ユニタリ行列L*が実行列の場合、単純にLの転置行列Ltになります。このとき、Lの対角成分はすべて“1”にできます。
\[
\begin{pmatrix}
a_{11} & \cdots & a_{1n}
\\
\vdots & \ddots & \vdots
\\
a_{n1} & \cdots & a_{nn}
\end{pmatrix}
=
\begin{pmatrix}
1 & & & O
\\
l_{21} & \ddots & &
\\
\vdots & \ddots & \ddots &
\\
l_{n1} & \cdots & l_{n,n-1} & 1
\end{pmatrix}
\begin{pmatrix}
d_{11} & & O
\\
& \ddots &
\\
O & & d_{nn}
\end{pmatrix}
\begin{pmatrix}
1 & l_{21} & \cdots & l_{n1}
\\
& \ddots & \ddots & \vdots
\\
& & \ddots & l_{n,n-1}
\\
O & & & 1
\end{pmatrix}
\]
この式を成分計算することで、次の関係式を得ます。
\[
\begin{eqnarray}
& \sum_{j=1}^i l_{kj} \ d_{jj} \ l_{ij} = a_{kj} \quad ( k \gt i )
\\
& \sum_{j=1}^k l_{kj} \ d_{jj} \ l_{kj} = a_{kk} \quad ( k \gt i )
\end{eqnarray}
\tag{4.3-1}
\]
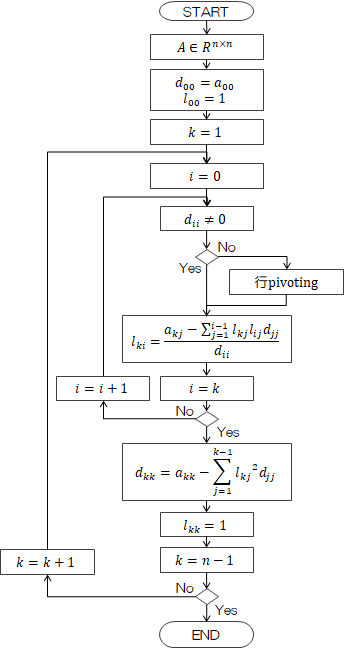
ここで\( l_{ii} = 1 \)として上記計算を行えばL、Dが定まります。\[
\begin{eqnarray}
& l_{ki}
& =
a_{kj} - \sum_{j=1}^{i-1} l_{kj} \ d_{jj} \ l_{ij} \quad ( i \lt k)
\\
& d_{kk}
& =
a_{kk} - \sum_{j=1}^{i-1} l_{kj}^2 \ d_{jj} \quad (i = k)
\end{eqnarray}
\tag{4.3-3}
\]
以上が修正コレスキー分解の計算方法になります。この計算フローは次の通りです (なお、プログラムを記述する際、添数は0から始めるのが一般的ですので、それに基づき記述します)。