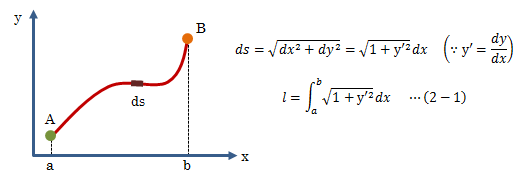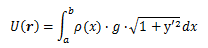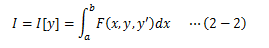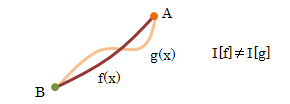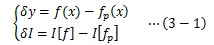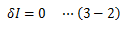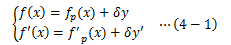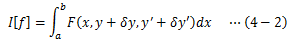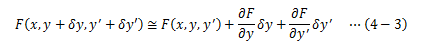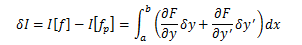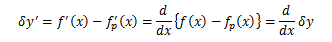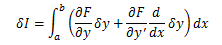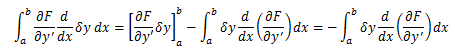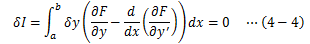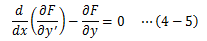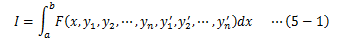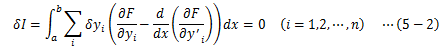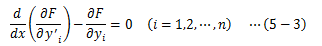1．変分原理の目的

物理法則や幾何学的法則では、次の一般的な表現が当てはまるケースが非常に多くあります。

ある量が極小（最小）または極大（最大）になるように変化は生じる

これを数学的に表現したものが変分原理になります。
変分原理の肝は、 「ある平衡状態に対し、ほんの少しずらしたらどうなる？」 といった視点からアプローチすることにあります。

2．汎関数（作用）

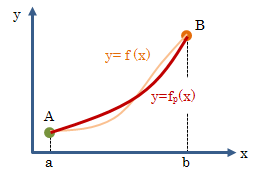
変分原理は多次元（多自由度）で成立しますが、まずは簡単のため2次元平面で話を進めます。
今、曲線y＝f(x)が区間a≦x≦bで微分可能とします。 このとき、曲線y＝f(x)の区間内での長さは次のように表現できます。

この曲線f(x)に対し、何かしらの量（例えば密度等）で重みづけされた形で現象を解くことが一般的です。 （例）AB間の鎖の重力ポテンシャル

このように、曲線y＝f(x)の関係を持った上で定義された関数F(x,y,y’)について、 xのある区間（[a,b]）で積分した関数を 汎関数（解析力学では、この汎関数を作用と呼びます）とよび、 次のように表します。

I[y]の表記は、y=f(x)の関数形によって積分Iは異なる値を示す、つまりIは経路に依存することを表しています。

3．変分

今問題にしているのは、この項の最初に述べた“極小または極大”です。 関数y＝f(x)が極値をとるとき、その1階微分はf’(x)＝0になります。 よって、極値近傍のxを微小量dxだけ変化させても、それに対応するdyは dy／dx＝0ゆえdy＝0^※になります。

※実際は停留値（極小、極大、変曲点）になります。 そこで、汎関数Iに極値を与えるf(x)をfp(x)とし、その時の汎関数をI[fp]で表します。

そこからわずかにずれた関数f(x)で決まる汎関数I[f]とI[fp]の差について考えてみます。

今、この関数の差をδy、汎関数の差をδIとけば、

で表せます。このδy、δIをそれぞれf(x)およびIの変分と呼びます。 今、Iが極値を取る場合を考えているので変分δIは“0” でなければなりません。

4．オイラーの方程式

今度は、汎関数Iが極値をとるための関数F(x,y,y’)の条件式を求めます。
関数f(x)はIに極値を与えるfp(x)からほんの少しずれたものであるため、 そのずれδyを用いて次のように表せます。

このf(x)を用いて計算した汎関数I[f]は次のようになります。

この被積分関数は、テイラー展開し、微小値δy、δy’の2次以降を無視することで 次のように書き換えられます。

ここで（4－2）式に（4－3）式を適用して変分δIを計算します。

このとき以下の関係式

を代入すれば、

となります。 さらに、右辺第二項に部分積分法を適用すると、点A、Bでのずれδy＝0ゆえ、

となるので、変分δIは次のようになります。

ところで、δyは任意ゆえ上式を恒等的に成立させるためには、被 積分関数が常に“0”になることが必要となります。

この式を、変分δI＝0に対するオイラーの方程式と呼びます。

5．多次元への展開

ここまでは、2次元に関する変分問題を扱いましたが、これはn次元へ簡単に拡張できます。 （2－2）式は次のように拡張されます。

この汎関数を前述同様にして変分δIを求めると、次のようになります。

各δyiは任意性を持つので、その各係数ごとに“0”とならなければなりません。

以上より、汎関数Iが極値を取る 関数F(x,y₁,y₂,…,y’₁,y’₂,…)は （5－3）式で表されるn個の2階微分方程式で決定されます。

参考文献

関連ページ