statsmodelsで回帰分析
1.サンプルファイルと使い方
Pythonの拡張ライブラリであるstatsmodelsを使って(重)回帰分析を行います。サンプルファイルはそのまま使えるようになっていますので、ご活用ください。
サンプルファイルの使い方は以下の通りです。
(2)データの書き換え
“sample1.csv”の中身を解析したいデータに書き換えます。- 一列目は目的変数、二列目以降は説明変数を入力します。
- 一行目は変数名を入力します。
- 二行目以降にデータを入力します。
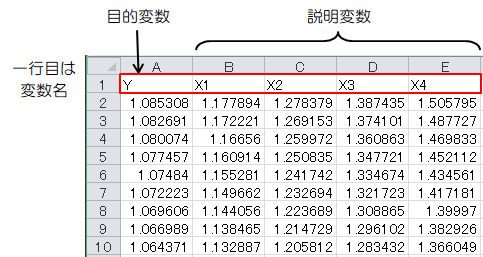
図1-1 sample1.csvの書き換え
(3)stats_ols.pyの実行
“stats_ols.py”と“sample1.csv”は同じフォルダに保存します。コマンドプロンプトを起動し、“stats_ols.py”を保存しているフォルダ(ディレクトリ)に移動します。例えば、Desktopなら下記を入力し、実行します。
>cd C:\Users\“ユーザー名”\Desktop
フォルダ(ディレクトリ)移動できたら、下記コマンドを実行します。
>python stats_ols.py
計算結果がコマンドプロンプト上に表示されます。
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 1.000
Model: OLS Adj. R-squared: 1.000
Method: Least Squares F-statistic: 1.686e+15
Date: Tue, 30 Jan 2018 Prob (F-statistic): 1.13e-228
Time: 22:47:13 Log-Likelihood: 690.03
No. Observations: 37 AIC: -1370.
Df Residuals: 32 BIC: -1362.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.2074 0.000 1086.878 0.000 0.207 0.208
x1 1.9284 0.002 1087.972 0.000 1.925 1.932
x2 -1.8590 0.003 -544.288 0.000 -1.866 -1.852
x3 0.8958 0.002 363.072 0.000 0.891 0.901
x4 -0.1726 0.001 -272.473 0.000 -0.174 -0.171
==============================================================================
Omnibus: 3.626 Durbin-Watson: 0.459
Prob(Omnibus): 0.163 Jarque-Bera (JB): 1.599
Skew: -0.039 Prob(JB): 0.450
Kurtosis: 1.984 Cond. No. 3.41e+07
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 2.01e-13. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
定数項推定値:0.207370727578, σ=0.000190794871681, P値=1.1759951337e-74
b'X1'推定値:1.92844618449, σ=0.00177251424107, P値=1.13872989565e-74
b'X2'推定値:-1.85900267551, σ=0.00341547739531, P値=4.7987564024e-65
b'X3'推定値:0.895813231997, σ=0.00246731506181, P値=2.02751334422e-59
b'X4'推定値:-0.17262747082, σ=0.000633556952829, P値=1.97283208233e-55
決定係数R21.0
自由度補正済み決定係数1.0
2.サンプルコード
サンプルファイル“stats_ols.py”の中身について説明していきます。本節最後にサンプルファイルの中身を掲載します。
(1)ライブラリのimport
import numpy as np import statsmodels.api as sm
(2)sample1.csvからデータ読み込み
sample1.csvはstats_ols.pyと同じフォルダに保存するので、パスは.//sample1.csvで指定します。読み込んだデータはNumpy形式の配列(配列名csvData)で取得します。 一行目の変数名も取得するので“dtype=None”とします。
csvFP = './/sample1.csv' csvData=np.genfromtxt(csvFP, dtype=None, delimiter=",", filling_values=(0))
(3)変数名を配列に引き当て
varNameに変数名を引き当て、確認のためコマンドプロンプトにvarNameの中身を表示します。varName=csvData[0] print (varName)
(4)変数操作
配列csvDataの一行目データ(変数名)を削除します。 さらに、残ったcsvDataを数値データに変換します。varName=csvData[0] print (varName)
(5)目的変数と説明変数に振り分け
配列csvDataを、目的変数Yobjと説明変数Xvarに振り分けます。さらに、定数項用に1のみの配列Xexpを作成し、XexpにXvarを追加します。
Yobj = csvData[:,0] Xvar = np.delete(csvData, 0, 1) Xexp=np.ones((len(Xvar),1)) Xexp=np.hstack((Xexp, Xvar)) print (Yobj) print (Xexp)
[[ 1. 1.17789443 1.27837878 1.38743529 1.50579524] [ 1. 1.17222056 1.26915306 1.37410104 1.48772731] [ 1. 1.16656037 1.25997181 1.3608631 1.46983319] [ 1. 1.16091387 1.25083493 1.34772102 1.45211162] [ 1. 1.15528106 1.24174231 1.33467432 1.43456137] [ 1. 1.14966193 1.23269384 1.32172255 1.41718117] [ 1. 1.14405649 1.22368941 1.30886524 1.3999698 ] [ 1. 1.13846473 1.21472892 1.29610194 1.38292603] [ 1. 1.13288666 1.20581226 1.28343218 1.36604862] [ 1. 1.12732228 1.19693932 1.27085551 1.34933635] [ 1. 1.12177158 1.18810999 1.25837147 1.33278802] [ 1. 1.11623457 1.17932418 1.24597961 1.31640241] [ 1. 1.11071125 1.17058176 1.23367947 1.30017833] [ 1. 1.10520161 1.16188264 1.2214706 1.28411456] [ 1. 1.09970566 1.1532267 1.20935254 1.26820993] [ 1. 1.0942234 1.14461385 1.19732485 1.25246325] [ 1. 1.08875482 1.13604396 1.18538707 1.23687335] [ 1. 1.08329994 1.12751694 1.17353875 1.22143903] [ 1. 1.07785874 1.11903268 1.16177946 1.20615915] [ 1. 1.07243123 1.11059107 1.15010874 1.19103254] [ 1. 1.0670174 1.102192 1.13852614 1.17605804] [ 1. 1.06161727 1.09383537 1.12703122 1.16123451] [ 1. 1.05623082 1.08552106 1.11562355 1.1465608 ] [ 1. 1.05085806 1.07724898 1.10430267 1.13203577] [ 1. 1.04549899 1.06901901 1.09306814 1.1176583 ] [ 1. 1.04015361 1.06083105 1.08191953 1.10342724] [ 1. 1.03482192 1.05268498 1.0708564 1.08934149] [ 1. 1.02950391 1.04458071 1.05987831 1.07539993] [ 1. 1.0241996 1.03651813 1.04898482 1.06160145] [ 1. 1.01890897 1.02849712 1.03817549 1.04794494] [ 1. 1.01363203 1.02051758 1.0274499 1.03442931] [ 1. 1.00836879 1.01257941 1.01680761 1.02105347] [ 1. 1.00311923 1.00468249 1.00624819 1.00781632] [ 1. 0.99788336 0.99682672 0.9957712 0.9947168 ] [ 1. 0.99266118 0.98901199 0.98537622 0.98175381] [ 1. 0.98745269 0.9812382 0.97506282 0.9689263 ] [ 1. 0.98225789 0.97350523 0.96483057 0.9562332 ]]
(6)重回帰分析
statsmodels関数“sm.OLS(説明変数, 目的変数)”により重回帰分析を行います。配列型は上記出力結果を参考にしてください。
results = sm.OLS(Yobj, Xexp).fit()
(7)重回帰分析の結果
回帰分析の結果サマリは.summary()を指定します。 .summary()の内容は、1.節の計算結果を参照ください。print (results.summary())
- 回帰係数:.param[*]
- 回帰係数のσ:.bse[*]
- 回帰係数のP値:.pvalues[*]
- 回帰係数のt値:.tvalues[*]
print("定数項推定値:"+str(results.params[0])+", σ="+str(results.bse[0])+", P値="+str(results.pvalues[0]))
for cnt1 in range(1, len(results.params)):
print(str(varName[cnt1])+"推定値:"+str(results.params[cnt1])+", σ="+str(results.bse[cnt1])+", P値="+str(results.pvalues[cnt1]))
print("決定係数R2"+str(results.rsquared))
print("自由度補正済み決定係数"+str(results.rsquared_adj))
#*******************************************************************************
#
#statsmodelsで回帰計算
#
#*******************************************************************************
import numpy as np
import statsmodels.api as sm
#csvからデータ読み込み =====================================
#stats_ols.pyと同じフォルダにsample1.csvファイルを置く
csvFP = './/sample1.csv'
#numpyでcsvファイル読み込み
csvData=np.genfromtxt(csvFP, dtype=None, delimiter=",", filling_values=(0))
#変数名取得
# バイト列で取得→b'xxx'で表示
varName=csvData[0]
print (varName)
#変数処理
# 変数名を削除
csvData=np.delete(csvData,0,0)
#バイト列→float型に変更
csvData=np.array(csvData, dtype=float)
#目的変数設定
Yobj = csvData[:,0]
#説明変数配列設定
Xvar = np.delete(csvData, 0, 1)
#重回帰 ====================================================
#定数項対応列付加
Xexp=np.ones((len(Xvar),1))
Xexp=np.hstack((Xexp, Xvar))
#確認用表示
print (Yobj)
print (Xexp)
#重回帰計算
results = sm.OLS(Yobj, Xexp).fit()
#結果サマリ表示
print (results.summary())
#回帰係数表示
# .params[] :回帰係数
# .base[] :σ
# .pvalues :P値
print ("\n")
print("定数項推定値:"+str(results.params[0])+", σ="+str(results.bse[0])+", P値="+str(results.pvalues[0]))
for cnt1 in range(1, len(results.params)):
print(str(varName[cnt1])+"推定値:"+str(results.params[cnt1])+", σ="+str(results.bse[cnt1])+", P値="+str(results.pvalues[cnt1]))
print ("\n")
#決定係数 / 自由度補正決定係数
print("決定係数R2"+str(results.rsquared))
print("自由度補正済み決定係数"+str(results.rsquared_adj))


