コラム
軸性ベクトルと極性ベクトル
作成日：20200709 テーマ1：科学 テーマ2：数学 テーマ3：ベクトル
（1）座標系の反転
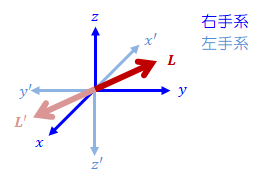
三次元座標系は、右手系と左手系の二種類がある。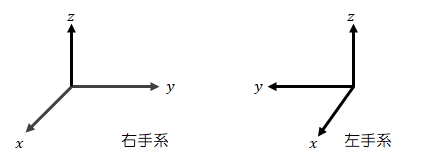
これらは、原点Oを基準にどう回転させても一致しない（鏡像関係）。
ただし、軸ごとに符号を反転させれば一致させられる（上図の場合、y軸の符号を反転）。
ここで、軸反転させるとどうなるかを見てみよう。
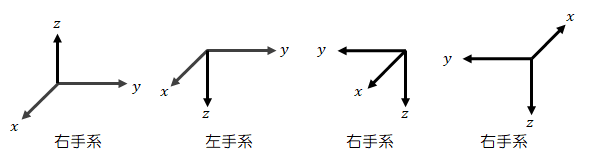
（2）軸性ベクトルと極性ベクトルの定義
軸性ベクトルと極性ベクトルは、この座標系の反転に対する振る舞いによって、次のように定義される。- 軸性ベクトル：反転に対してベクトル成分の符号は反転しない（擬ベクトルともいう）
- 極性ベクトル：反転に対してベクトル成分の符号も反転する
（3）極性ベクトルの特徴
まずは極性ベクトルについて、軸単位ベクトル（正規直交基底ベクトル）を \((\bf{e_x}, \bf{e_y}, \bf{e_z})\) とする座標系O-XYZに対し、3つの軸をすべて符号反転した座標系O-X'Y'Z'のそれは
\[
(\bf{e_x'}, \bf{e_y'}, \bf{e_z'}) = (-\bf{e_x}, -\bf{e_y}, -\bf{e_z})
\]
になる。
O-XYZ系から見た極性ベクトルを\(\bf{p}\)、O-X'Y'Z'系から見た極性ベクトルを\(\bf{p'}\)で表すと、極性ベクトルの定義から、それぞれの成分は次のように表せる。
\[
\begin{eqnarray}
& \bf{p} &= (x, y, z)^t
\\
& \bf{p'} &= (x', y', z')^t = (-x, -y, -z)^t
\end{eqnarray}
\]
このとき次の計算によって、を\(\bf{p} = \bf{p'}\)の関係が得られる。
\[
\begin{eqnarray}
\bf{p'} & = & x' \bf{e_x'} + y' \bf{e_y'} + z'\bf{e_z'}
\\
& = & (-x)(-\bf{e_x}) + (-y)(-\bf{e_y}) + (-z)(-\bf{e_z})
\\
& = & x\bf{e_x} + y\bf{e_y} + z\bf{e_z}z
\\
& = & \bf{p}
\end{eqnarray}
\]
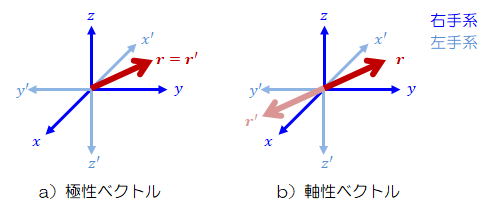
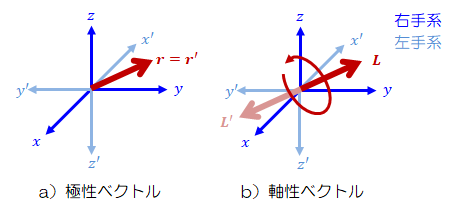
これは、極性ベクトルは空間に固定されたものであって、座標系の反転に対して不変であることを意味する
（上図a）を参照）。
（4）軸性ベクトルの特徴
次に軸性ベクトルについて、さきほどの座標系O-XYZから見た軸性ベクトル\( \bf{a} \)と、3つの軸をすべて符号反転した座標系O-X'Y'Z'のから見た軸性ベクトル\( \bf{a'} \)で表すと、軸性ベクトルの定義から、それぞれの成分は次のように表せる。
\[
\begin{eqnarray}
& \bf{a} &= (x, y, z)^t
\\
& \bf{a'} &= (x', y', z')^t = (x, y, z)^t
\end{eqnarray}
\]
このとき次の計算によって、を\(\bf{a} = -\bf{a'}\)の関係が得られる。
\[
\begin{eqnarray}
\bf{a'} & = & x' \bf{e_x'} + y' \bf{e_y'} + z'\bf{e_z'}
\\
& = & x(-\bf{e_x}) + y(-\bf{e_y}) + z(-\bf{e_z})
\\
& = & -\bf{a}
\end{eqnarray}
\]
これは、軸性ベクトルは座標系に固定されたものであって、座標系の反転に伴い空間に対して反転することを意味する（上図b）を参照）。
（5）軸性ベクトルと極性ベクトルの具体例
（3）（4）の結論は、定義から当たり前の結果が得られただけなので、ここでは極性ベクトルと軸性ベクトル、それぞれの具体的な例について見ていくことにする。a）極性ベクトルの具体例
極性ベクトルは空間に固定されたベクトルであるから、最もイメージしやすいのは位置ベクトルであろう。例えば大阪 - 東京を結んだベクトルがあるとする。 座標系は、右手、左手関係なく、地球上に無数に設定できるが、大阪 - 東京を結んだベクトル自体は何も変わらない。 なぜなら、大阪、東京の地点は座標系に関係なく存在するから．．．。
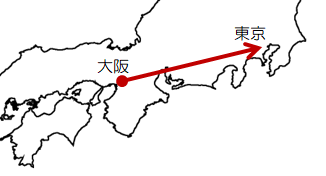このように、空間に対して向きが決まるベクトル、位置ベクトル、速度ベクトル、力ベクトルなどが極性ベクトルにあてはまる。
b）軸性ベクトルの具体例
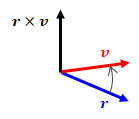
では、座標系に固定された軸性ベクトルっていったい・・・？ということで、まずは角運動量について見てみよう（なんで角運動量かは後でわかる）。 角運動量\( \bf{L} \)は位置ベクトル\( \bf{r} \)と運動量ベクトル\( \bf{p} \)の外積によって決まる。
\[
\bf{L} = \bf{r} \times \bf{p} = m \bf{r} \times \bf{v}
\]
結局は\( \bf{r} \)と\( \bf{v} \)の外積なので、これを成分計算する。
まずは右手系O-XYZの成分計算を行う。 このとき、 \( \bf{e_i} \times \bf{e_i} = \bf{o} \)、 \( \bf{e_x} \times \bf{e_y} = \bf{e_z} \)、 \( \bf{e_y} \times \bf{e_x} = -\bf{e_z} \cdots \)を考慮すると
\[
\begin{eqnarray}
\bf{r} \times \bf{p}
& = & ( x \bf{e_x} + y \bf{e_y} + z \bf{e_z} ) \times
( v_x \bf{e_x} + v_y \bf{e_y} + v_z \bf{e_z})
\\
& = & (y v_z - z v_y)\bf{e_x} + (z v_x - x v_x)\bf{e_y} + (x v_y - y v_x)\bf{e_z}
\end{eqnarray}
\]
次に左手系O-X'Y'Z'の成分計算を行う。
\[
\begin{eqnarray}
\bf{r} \times \bf{p}
& = & ( x \bf{e_x'} + y \bf{e_y'} + z \bf{e_z'} ) \times
( v_x \bf{e_x'} + v_y \bf{e_y'} + v_z \bf{e_z'})
\\
\\
& = & (y v_z - z v_y)\bf{e_x'} + (z v_x - x v_x)\bf{e_y'} + (x v_y - y v_x)\bf{e_z'}
\end{eqnarray}
\]
両式を比べると成分は一致するが、軸単位ベクトルは反転するので、
\[
\bf{r'} \times \bf{v'} = \bf{r} \times \bf{v}
\\
\\
\rightarrow \bf{L'} = -\bf{L}
\]
つまり角運動量ベクトルは軸性ベクトルであり、座標系の反転に伴い、空間に対して反転する。
このことは一体何を意味するのか？
角運動量は回転運動を表すためのものである。 回転には時計周り、反時計回りといった向きが存在する。
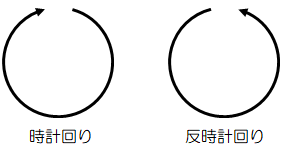ただ、同じ回転でも見る方向によっては、時計回りにも反時計回りにもなってしまう。
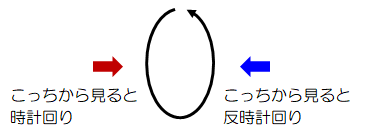それでは非常に都合が悪い。
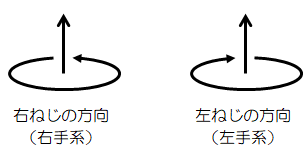
ということで「右ねじを回転させるとねじが進む方向」という形で定義すれば、回転方向は一意に決まる
（回転と見る方向を同時に決める）。
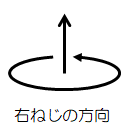ベクトルの外積の向きは、この右ねじの方向（右手系）によって決められている。
右手系O-XYZの角運動量ベクトルLに対する回転方向を図示すると、次のようになる。
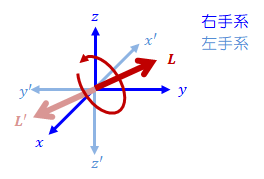反転座標系O-X'Y'Z'は左手系なので、角運動量ベクトルL'の向きは、右ねじではなく“左ねじ”に従うことになる。
つまり、座標系の反転は同じ回転について見る方向が変わっただけであり、軸性ベクトルで決められる「回転の向きは空間に対し不変」である。
このように、回転の向きが空間に固定される角運動量ベクトル、角速度ベクトル、モーメントベクトル等が軸性ベクトルにあてはまる。
- 極性ベクトルで決められるベクトルの向きは、座標の反転に影響されず空間に固定される
- 軸性ベクトルで決められる回転の向きは、座標の反転に影響されず空間に固定される
（6）演算の組み合わせ
先ほどの話に戻ると、角運動量\( \bf{L} \)は軸性ベクトル、位置ベクトル\( \bf{r} \)と速度ベクトル\( \bf{v} \)は極性ベクトルである。 ということは、極性ベクトル同士の掛け算は軸性ベクトルになっている。となると、軸性ベクトルと極性ベクトルの外積、内積についてどのような結果が得られるであろうか？
ここでは答えだけを載せておく。
＜外積＞
- 軸性ベクトル×軸性ベクトル = 軸性ベクトル
- 軸性ベクトル×極性ベクトル = 極性ベクトル
- 極性ベクトル×軸性ベクトル = 極性ベクトル
- 極性ベクトル×極性ベクトル = 軸性ベクトル
＜内積＞
- 軸性ベクトル・軸性ベクトル = スカラー
- 軸性ベクトル・極性ベクトル = 擬スカラー
- 極性ベクトル・軸性ベクトル = スカラー
- 極性ベクトル・極性ベクトル = 擬スカラー
