コラム
微分と積分（微分編）
作成日：20190515 テーマ1：科学 テーマ2：数学 テーマ3：
ここでは厳密ではないけども“微分”と“積分”の意味がわかる程度の説明を行う。
まずは関数\(f(x)=x^2 \)を例にとって“微分”について考えてみよう。
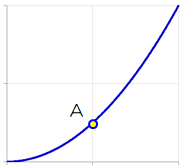\( x=x_a \)での\( f(x) = x^2 \)の点\( (x_a, x_a^2) \)をAとする。
この点Aの近傍に点A'をとり、その座標を\( (x_a+dx, (x_a+dx)^2) \)とする。
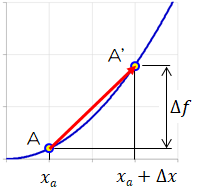
このとき、\( f(x) \)の変化\( \Delta f \)は次のようになる。
この操作は、関数を「微小区間に分割」し、その範囲での変化率を求めるものである。
ところで、この\( \Delta x \)を徐々に小さくしていくとどうなるだろうか？
\( \Delta x \)を小さくすることで、関数\( f(x) \)と線部AA'の乖離が徐々に小さくなっていくことがわかる。
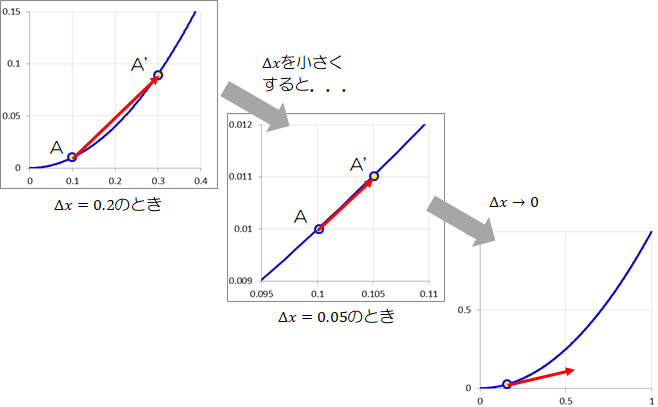であれば、\( \Delta x \)を0に限りなく近づければ\( f(x) \) とAA'の乖離はなくなるはずである。
これはつまり、（2）式は点Aでの接線の傾きを表すことに他ならない。
なお、このとき行った「\( \Delta x \)を0に限りなく近づける」操作は「\( \Delta x \)を∞に小さくする」ことと同じである。 このときの区間 \( \Delta x \)を無限小区間と呼ぶ。また、数学では「変数\(x\)をある値\(c\)に限りなく近づける」を“\(x \rightarrow c \)”で表す。
ここで（2）式に立ち返る。\( \Delta x \rightarrow 0 \)としているので
なお、微分の具体的な計算方法は数学の教科書に譲る。
以上の話をまとめよう。 “微分”とは、関数\( f(x) \)を限りなく0に近い微小区間で分割し、その区間ごとの変化率\( \Delta f / \Delta x \)を求めることで、その結果\( f(x) \)の接線が定まる。
ということで「何かしらの変動を求めたい」と思ったら、まずは“微分”を思い出そう。
まずは関数\(f(x)=x^2 \)を例にとって“微分”について考えてみよう。
\( x=x_a \)での\( f(x) = x^2 \)の点\( (x_a, x_a^2) \)をAとする。
この点Aの近傍に点A'をとり、その座標を\( (x_a+dx, (x_a+dx)^2) \)とする。
このとき、\( f(x) \)の変化\( \Delta f \)は次のようになる。
\[
\Delta f
=
f(x_a + dx) - f(x_a)
=
2x_a \Delta x + \Delta x^2
\tag{1}
\]
従って、線分AA'の傾きは
\[
\frac{ \Delta f }{ \Delta x }
=
\frac{ f(x_a + dx) - f(x_a) }{ \Delta x }
=
2x_a + \Delta x
\tag{2}
\]
となる。
この操作は、関数を「微小区間に分割」し、その範囲での変化率を求めるものである。
ところで、この\( \Delta x \)を徐々に小さくしていくとどうなるだろうか？
\( \Delta x \)を小さくすることで、関数\( f(x) \)と線部AA'の乖離が徐々に小さくなっていくことがわかる。
であれば、\( \Delta x \)を0に限りなく近づければ\( f(x) \) とAA'の乖離はなくなるはずである。
これはつまり、（2）式は点Aでの接線の傾きを表すことに他ならない。
なお、このとき行った「\( \Delta x \)を0に限りなく近づける」操作は「\( \Delta x \)を∞に小さくする」ことと同じである。 このときの区間 \( \Delta x \)を無限小区間と呼ぶ。また、数学では「変数\(x\)をある値\(c\)に限りなく近づける」を“\(x \rightarrow c \)”で表す。
ここで（2）式に立ち返る。\( \Delta x \rightarrow 0 \)としているので
\[
\Delta x \rightarrow 0
ならば
\frac{ \Delta f }{ \Delta x }
\simeq
2x_a
\tag{3}
\]
である。
ここで“\( \simeq \)”はだいたい同じ、つまり近似的に“=”の意味である。
なぜなら\( \Delta x \rightarrow 0 \)（限りなく近づける）であり、\( \Delta x = 0 \)とは言っていないためである。
（3）式は点Aでの接線の傾きを表している。
\( x_a \)は特別な値を指定しているわけではなく、任意の値をとることができる。
従って、あえて\( x_a \)を使う必要はなく\( x \)で表しても問題ない。
あえて書けば、
\[
\Delta x \rightarrow 0
ならば
\frac{ \Delta f }{ \Delta x }
\simeq
2x
\tag{4}
\]
である。
この（4）式の関係を“微分”と呼んでいる。
微分の数学的な表記は次のようになる。
\[
f'(x)
=
\frac{ df(x) }{ dx }
=\displaystyle \lim_{ n \to 0 } \frac{ \Delta f }{ \Delta x }
\tag{5}
\]
上記三つのどれを用いても構わないが、簡略表記したい場合は\( f'(x) \)、何の変数で微分したかを明示したい場合は\( df / dx \)を用いる。
なお、微分の具体的な計算方法は数学の教科書に譲る。
以上の話をまとめよう。 “微分”とは、関数\( f(x) \)を限りなく0に近い微小区間で分割し、その区間ごとの変化率\( \Delta f / \Delta x \)を求めることで、その結果\( f(x) \)の接線が定まる。
ということで「何かしらの変動を求めたい」と思ったら、まずは“微分”を思い出そう。
