コラム
%E6%9B%B2%E9%9D%A2%E3%81%AE%E6%8E%A5%E5%B9%B3%E9%9D%A2%E3%81%AE%E6%B1%82%E3%82%81%E6%96%B9
作成日：20200215 テーマ1：%E7%A7%91%E5%AD%A6 テーマ2：%E6%95%B0%E5%AD%A6 テーマ3：
曲面の法線ベクトルと接平面は簡単に求めることができます。
三次元空間上の任意の曲面はf(x,y,z)=0で表せます。 今、この曲面f上の近接する2点A:(xo,yo,zo)とB:(xo+dx,yo+dy,zo+dz)に着目します。
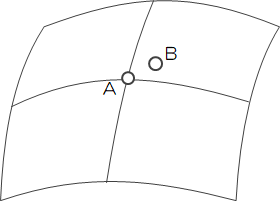点Bは点Aの近接点なのでdx, dy, dzは微小値であり、（1）下の式は点A周りでテイラー展開できます。
ここで、新たに次のベクトルを定義します。
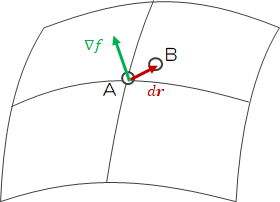ただし、\(\nabla f_o \)は点Aでの\(\nabla f \)の値を示します。
ここでdrを0に極限まで近づけると、\( O ( \Delta^2 ) \)もまた0に近づき、drは曲面fの接線ベクトルになります。 すると、\( \nabla f_o d \boldsymbol{ r } \)も0に近づくことから、\(\nabla f_o \)は点Aで\(\nabla f \)に直交することになります。 以上のことから
次に曲面fの接平面を求めます。
点(xo,yo,zo)を通る任意の平面は次式で表せます。
また、この考えは曲線の接線を求める場合にも使えます。 この場合はzを消すだけで終わりです。
曲線\( f(x,y)=0 \)に対して、点(xo,yo)での接線は
\( y = x^2-5 \)の点\((x_o,y_o)\)での接線を求めます。
（2）\( x_o = 1 \)の場合、\( y_o = -4 \)なので、（*）式に代入して
三次元空間上の任意の曲面はf(x,y,z)=0で表せます。 今、この曲面f上の近接する2点A:(xo,yo,zo)とB:(xo+dx,yo+dy,zo+dz)に着目します。
\[
\begin{eqnarray}
& f & (x_o, y_o, z_o) = 0
\\
& f & (x_o + dx, y_o +dy , z_o +dz ) = 0
\end{eqnarray}
\tag{1}
\]
点Bは点Aの近接点なのでdx, dy, dzは微小値であり、（1）下の式は点A周りでテイラー展開できます。
\[
\begin{eqnarray}
f(x_o + dx, y_o +dy , z_o +dz )
& = &
f(x_o, y_o, z_o) +
\left. \frac{\partial f}{\partial x} \right|_o dx +
\left. \frac{\partial f}{\partial y} \right|_o dy +
\left. \frac{\partial f}{\partial z} \right|_o dz
+O ( \Delta^2 )
\\
& = &
\left. \frac{\partial f}{\partial x} \right|_o dx +
\left. \frac{\partial f}{\partial y} \right|_o dy +
\left. \frac{\partial f}{\partial z} \right|_o dz
+O ( \Delta^2 )
\end{eqnarray}
\tag{2}
\]
なお、\( \left. \frac{\partial f}{\partial x} \right|_o \)はxoでの偏微分の値を示します。
ここで、新たに次のベクトルを定義します。
\[
\begin{eqnarray}
\nabla f
=
\left(
\begin{array}{c}
\displaystyle \frac{\partial f}{\partial x}
\\
\displaystyle \frac{\partial f}{\partial y}
\\
\displaystyle \frac{\partial f}{\partial z}
\end{array}
\right)
, \quad
d \boldsymbol{ r }
=
\left(
\begin{array}{c}
dx
\\
dy
\\
dz
\end{array}
\right)
\end{eqnarray}
\tag{3}
\]
すると、（2）式は\( \nabla f \)とdrの内積を使って表すことができます。
\[
f(x_o + dx, y_o +dy , z_o +dz )
=
\nabla f_o d \boldsymbol{ r } + O ( \Delta^2 )
\tag{4}
\]
ただし、\(\nabla f_o \)は点Aでの\(\nabla f \)の値を示します。
ここでdrを0に極限まで近づけると、\( O ( \Delta^2 ) \)もまた0に近づき、drは曲面fの接線ベクトルになります。 すると、\( \nabla f_o d \boldsymbol{ r } \)も0に近づくことから、\(\nabla f_o \)は点Aで\(\nabla f \)に直交することになります。 以上のことから
“\(\nabla f \)は曲面fの法線ベクトル”
であることがわかります。次に曲面fの接平面を求めます。
点(xo,yo,zo)を通る任意の平面は次式で表せます。
\[
A(x-x_o)+B(y-y_o)+C(z-z_o)=0
\tag{5}
\]
この平面の法線ベクトルが、先ほどの曲面fの法線ベクトル\(\nabla f_o \)と一致すれば、点(xo,yo,zo)におけるfの接平面であることは明らかです。
従って、
\[
A=\left. \frac{\partial f}{\partial x} \right|_o,
B=\left. \frac{\partial f}{\partial y} \right|_o,
C=\left. \frac{\partial f}{\partial z} \right|_o
\]
であり、接平面は次のようになります。
\[
\left. \frac{\partial f}{\partial x} \right|_o (x-x_o) +
\left. \frac{\partial f}{\partial y} \right|_o (y-y_o) +
\left. \frac{\partial f}{\partial z} \right|_o C(z-z_o)
=0
\tag{6}
\]
このように偏微分の計算方法さえ知っていれば、曲面の接平面は非常に簡単に求めることができます。
また、この考えは曲線の接線を求める場合にも使えます。 この場合はzを消すだけで終わりです。
曲線\( f(x,y)=0 \)に対して、点(xo,yo)での接線は
\[
\left. \frac{\partial f}{\partial x} \right|_o (x-x_o) +
\left. \frac{\partial f}{\partial y} \right|_o (y-y_o)
=0
\]
では具体例を挙げて、接線を求めてみます。
\( y = x^2-5 \)の点\((x_o,y_o)\)での接線を求めます。
\[
f(x,y)=x^2-y-5
\]
なので、
\[
\frac{\partial f}{\partial x}=2x
, \quad
\frac{\partial f}{\partial y}=-1
\]
が得られます。
従って、点\((x_o,y_o)\)での接線は次のようになります。
\[
2x_o ( x- x_o ) - ( y - y_o ) =0
\tag{*}
\]
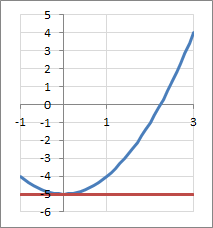
（1）\( x_o = 0 \)の場合、\( y_o = -5 \)なので、（*）式に代入して
\[
y=-5
\]
図示すると、次のようになります。
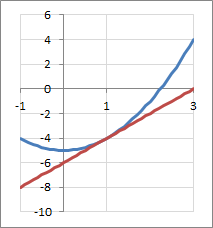
（2）\( x_o = 1 \)の場合、\( y_o = -4 \)なので、（*）式に代入して
\[
y=2x-6
\]
図示すると、次のようになります。
