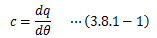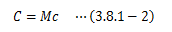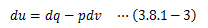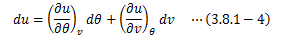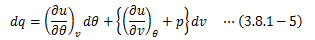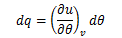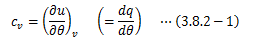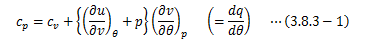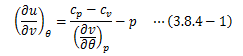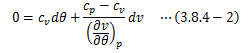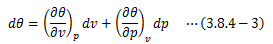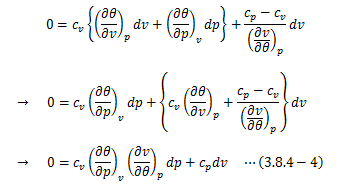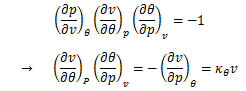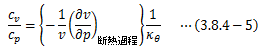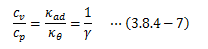熱力学

3．5．内部エネルギー

熱力学第一法則から内部エネルギーというものの存在を定義することができました。しかしながら、それがどういった意味を持つかまではその定義からは全くわかりません。そこで、内部エネルギーを微視的に見ることで、それが持つ意味について見ていくことにします。
系を構成しているのは分子であり、それは特別な場合を除き常に運動しています。運動エネルギーは速度の二乗に比例することから、分子は運動する限りエネルギーを所有します。また、分子は電荷を帯びた電子や陽子によって構成されているため、相互間力によるポテンシャルエネルギーも所有しています。これら微視的なエネルギーは、系、つまりマクロな運動エネルギーや位置エネルギー、つまり力学的エネルギーとは関係なく、系内部に蓄えているエネルギーと捉えることができます。さらに、系は運動していなくてもエネルギーを所有していることを意味します。これが内部エネルギーの持つ意味になります。

3．6．エネルギーの移動形態

ここでは、エネルギーの移動形態を表す“仕事”と“熱”によってエネルギーが移動する様を、微視的に見ることで明らかにしていきます。

3．6．1．仕事による移動

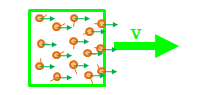
物体の運動は、物体そのものがある方向へ移動することです。このとき、物体を構成する全ての分子に、一様に物体と同じ方向に動く成分が加わります（物体の変形も同じです）。つまり、仕事では物体の構成分子には一様かつ等方にエネルギーが付与されることになります。

図3.6.1－1　仕事による移動

その結果仕事とは、物体の運動や変形によって生じる構成分子の一様かつ等方な運動によってエネルギーを移動させる、と言うことができます。

3．6．2．熱による移動

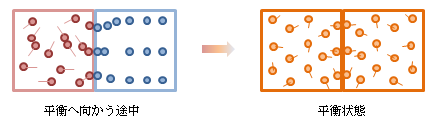
例として、熱い系Aと冷たい系Bを接触させた場合を考えます。このとき系Aの分子運動は活動的であり、Bの運動は非活動的になります。系Aと系Bは、その接触面で分子の衝突が繰り返されます。衝突はあらゆる方向で生じ、系内に伝播します。この衝突によってそれぞれの系の運動は平滑化され、最終的には系AとB両方の分子運動が同等、つまり温度が同等にまで変化し、そこで平衡状態に落ち着きます。

図3.6.2－1　熱による平衡状態の移動

このように熱によるエネルギーの移動は、分子運動のランダムな衝突によって行われ、仕事によるエネルギーの移動とは違い、分子衝突によって発生する力に打ち消し合いが生じ、系全体に運動が起こらない、と考えられます（厳密には、分子は運動エネルギー以外にも相互間作用によるポテンシャルも影響します）。
以上をまとめると熱とは、物体の構成分子に生じたランダムな運動を利用してエネルギーを移動させ、さらにはこの移動によって物体の温度勾配を生じること、と言えます。

3．7．熱量

熱量とは、標準大気圧下において1gの水を1℃上昇させるのに必要な熱エネルギーで、その量を1calと定義しています。ただし、熱量は温度によって変化するため、現在は14.5℃から15.5℃まで上昇させる熱エネルギーを1calとしています。また、ジュールの実験によって熱と仕事の等価性が証明され、仕事を表すJ（ジュール）と熱量を表すcal（カロリー）との関係が明らかにされました。