弾性論
2.1.変形とひずみ
物体の変形とはその内部の各点間距離が変化することです。 変位があっても距離が変化しなければ、物体は単に剛体運動しているだけになります。ここで物体の変形を数学的に表現することを試みます。
変形をうけた物体内の近接する任意の二点P、Q(位置ベクトルを\( \bf{ r } 、\bf{ r } + d\bf{ r } \))がP'、Q'に変位し、それぞれの変位ベクトル\( \bf{ u } ( \bf{ r } ) 、\bf{ u } ( \bf{ r } + d\bf{ r } ) \)とするとき、次式が成り立ちます。
\[
d\bf{ r' } - d\bf{ r }
= \bf{ u } ( \bf{ r } + d\bf{ r } ) - \bf{ u } ( \bf{ r } )
\tag{2.1-1}
\]
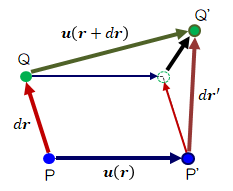
図2.1-1 物体の変形に伴う変位
\( d \bf{ r } \)は微小ゆえ、上式右辺をテイラー展開して二次以上の微小項を無視すると\[
\begin{align}
\bf{ u } ( \bf{ r } + d\bf{ r } ) - \bf{ u } ( \bf{ r } )
& \simeq \frac {\partial \bf{ u } ( \bf{ r } ) }{\partial \bf{ r } } d \bf{ r }
\\
&=
\left(
\begin{array}{ccc}
\displaystyle \frac {\partial u_x}{\partial x} &
\displaystyle \frac {\partial u_x}{\partial y} &
\displaystyle \frac {\partial u_x}{\partial z}
\\
\displaystyle \frac {\partial u_y}{\partial x} &
\displaystyle \frac {\partial u_y}{\partial y} &
\displaystyle \frac {\partial u_y}{\partial z}
\\
\displaystyle \frac {\partial u_z}{\partial x} &
\displaystyle \frac {\partial u_z}{\partial y} &
\displaystyle \frac {\partial u_z}{\partial z}
\end{array}
\right)
\left(
\begin{array}{c}
dx \\
dy \\
dz
\end{array}
\right)
\end{align}
\tag{2.1-2}
\]
となります。
この\( d \bf{ r } \)の係数行列を変形テンソルと呼び、その対角成分と非対角成分はそれぞれ次のような意味を持ちます。
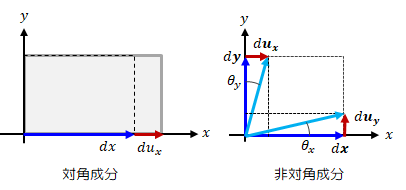
図2.1-2 変形テンソルの成分
対角成分は、例えば上図左側のように\( {\partial u_x } / {\partial x} \) ならx軸方向の伸縮率を表します。 非対角成分は微小変形を前提としているので、上図右側で設定した角度で表せます。\[
\begin{align}
& \theta_x
= \displaystyle \tan^{-1} \frac {\partial u_y}{\partial x}
\simeq \frac{\partial u_y}{\partial x}
\\
& \theta_y
= \displaystyle \tan^{-1} \frac {\partial u_x}{\partial y}
\simeq \frac{\partial u_x}{\partial y}
\end{align}
\tag{2.1-3}
\]
この関係は、後述するひずみテンソルの意味のところで必要となります。
さて、変形は物体内の各点間距離によって計られるので、(2.1-1)式を変形して二乗し、距離の関係式に書き直します(同時に成分表示に書き直します)。
\[
\begin{align}
{dx'_i}^2
&= dx_i^2 + 2 dx_i \frac{\partial u_i}{\partial x_j} dx_j
+ \left( \frac {\partial u_k}{\partial x_j} dx_j \right)^2
\\
&= dx_i^2 + \left(
\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}
+ \frac {\partial u_k}{\partial x_i} \frac {\partial u_k}{\partial x_j}
\right)
\\
&= 2 \epsilon_{ij} dx_i
dx_j \end{align}
\]
(∵テンソルの規約の性質)
ここで\( \epsilon_{ij} \)は次式であって、これをひずみテンソルと呼びます。
\[
\epsilon _{ij}
= \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}
+ \frac {\partial u_k}{\partial x_i} \frac {\partial u_k}{\partial x_j} \right)
\tag{2.1-5}
\]
ひずみテンソル\( \epsilon_{ij} \)が対称テンソル\( \epsilon_{ij} = \epsilon_{ji} \)であることは上式から明らかです。
また、通常物体の変形は微小であり、ひずみテンソルに含まれる二次の項を無視した次式が一般的なひずみテンソルの式となります。
\[
\epsilon _{ij}
= \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)
\tag{2.1-6}
\]
ここで、変形テンソルを対称テンソルと反対称テンソルに分解すると、
\[
\begin{align}
\frac {\partial u_j}{\partial x_i}
&= \frac{1}{2} \left( \frac {\partial u_j}{\partial x_i} + \frac {\partial u_i}{\partial x_j} \right)
+ \frac{1}{2} \left( \frac {\partial u_j}{\partial x_i} - \frac {\partial u_i}{\partial x_j} \right)
\end{align}
\]
対称テンソルはひずみテンソル(2.1-6)式に一致します。
反対称テンソルの方は結果から先に言うと物体の回転を表していて、回転テンソルと呼び\( \Omega_{ij} \)で表します。
ひずみテンソルと回転テンソルを成分表示すると、次のようになります。
\[
\begin{eqnarray}
\epsilon_{ij}
=
\left(
\begin{array}{ccc}
\epsilon_{xx} &
\epsilon_{xy} &
\epsilon_{xz} \\
\epsilon_{yx} &
\epsilon_{yy} &
\epsilon_{yz} \\
\epsilon_{zx} &
\epsilon_{zy} &
\epsilon_{zz}
\end{array}
\right)
\quad
\Omega_{ij}
=
\left(
\begin{array}{ccc}
0 &
\Omega_{xy} &
-\Omega_{xz} \\
-\Omega_{yx} &
0 &
\Omega_{yz} \\
\Omega_{zx} &
-\Omega_{zy} &
0
\end{array}
\right)
\end{eqnarray}
\tag{2.1-7}
\]
ここで、ひずみテンソルと回転テンソルの各成分が持つ意味について考えます。
なお考察を簡単にするため、xy平面内の変形に着目します。
ひずみテンソルの対角成分は変形テンソルの対角成分と一致するため、伸縮率の意味を持ちます。
\[
\epsilon_{xx} = \frac{\partial u_x}{\partial x}
、
\epsilon_{yy} = \frac{\partial u_y}{\partial y}
\]
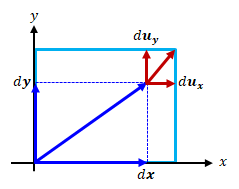
図2.1-3 ひずみテンソルの対角成分
次に、ひずみテンソルと回転テンソルの非対角成分について考えます。 変形テンソルの非対角成分は(2.1-3)式によって角度で表せたことから、ひずみテンソルと回転テンソルの非対角成分も角度で表せます。\[
\epsilon_{xy} = \frac{1}{2} ( \theta_x + \theta_y )
、
\Omega_{xy} = \frac{1}{2} ( \theta_x - \theta_y )
\tag{2.1-8}
\]
\( \theta_x + \theta_y = 0 \)の場合、ひずみテンソルの成分はすべて0なのに対し、回転テンソルの成分は\( \Omega_{xy} = \theta_x \)となります。
このとき、下図のように着目要素は形を変えず単に回転するだけです。
\[
\epsilon_{xy} = 0
、
\Omega_{xy} = \theta_x
\]
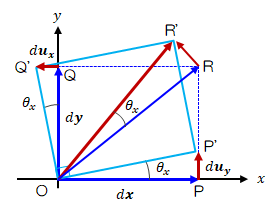
図2.1-4 回転テンソルの非対角成分
\( \theta_x - \theta_y = 0 \)の場合、回転テンソルの成分はすべて0なのに対し、ひずみテンソルの成分は\( \epsilon_{xy} = \theta_x \)となります。 このとき、下図のように着目要素は長方形から平行四辺形に変形します。 この変形をせん断変形またはずれ変形と呼びます。 また、ひずみテンソルの非対角成分をせん断ひずみと呼びます。\[
\epsilon_{xy} = \theta_x
、
\Omega_{xy} = 0
\]
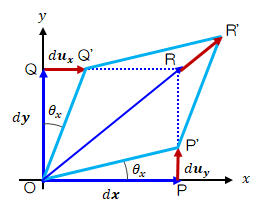
図2.1-5 ひずみテンソルの非対角成分
これらの詳細については連続体力学ページ2.3節に説明を譲ります。次に、体積ひずみを導入します。
ひずみテンソルは対称テンソルのため座標変換によって対角化できます。 この対角化を主軸変換と呼び、それぞれの座標軸を主軸と呼びます。 対角化したひずみテンソルを次のように表します。
\[
\epsilon_{ij}
=
\begin{eqnarray}\left(
\begin{array}{ccc}
\epsilon_{xx} &
0 &
0 \\
0 &
\epsilon_{yy} &
0 \\
0 &
0 &
\epsilon_{zz}
\end{array}
\right)\end{eqnarray}
\tag{2.1-9}
\]
このとき、物体の変形は主軸方向の伸長のみとなり、(2.1-1)式は
\[
|d \bf{r'} | ^2
= dx_i ^2 + 2 \epsilon_{ij} dx_i dx_j
= ( 1+ 2 \epsilon_{ij} ) dx_i^2
\tag{2.1-10}
\]
と書き換えられ、各主軸方向の相対伸びは微小変形による近似を考慮することで、主軸ひずみと一致します。
\[
\frac { dx_i'- dx_i }{ dx_i}
= \sqrt{ 1 + 2 \epsilon_i \ } - 1
\simeq \epsilon_i
\tag{2.1-11}
\]
\[
\left(
\because
\sqrt{ 1 + 2 \epsilon_i \ }
\simeq \sqrt{ (1 + \epsilon_i)^2 \ }
= 1 + \epsilon_i
\right)
\]
これをもとに、物体の体積素片\( dV \)に着目し、変形後の\( dV' \)を求めます。
主軸に対する\( dV = dx_1 dx_2 dx_3 \)は、変形後
\[
\begin{align}
dV'
&= ( 1 + \epsilon_1 ) dx_1 ( 1+ \epsilon_2 ) dx_2 ( 1 + \epsilon_3 ) dx_3
\\
& \simeq ( 1 + \epsilon_1 + \epsilon_2 + \epsilon_3 ) dV
\end{align}
\tag{2.1-12}
\]
になります。
ところで、テンソルの対角和\( ε_{ll} \)はテンソル不変量であり、非対角成分を含むテンソルの場合でも一定の値を取ります。
従って、物体の変形に伴う体積変化率は座標系に依存せず、またテンソルの対角和は体積ひずみとしての意味を持ちます。
\[
\frac { dV'- dV }{ dV } = \epsilon_{ll}
\\
( \epsilon_{ll} = \epsilon_{11} + \epsilon_{22} + \epsilon_{33} )
\tag{2.1-13}
\]
これとは逆に、非対角成分(せん断ひずみ)のみのひずみテンソルは、対角和\( ε_{ll} = 0 \)であるから物体の変形に伴う体積変化はありません。
2.2.応力
物体に働く力は大別すると次の二つに分類されます。- 体積力:物体の体積や質量に比例する力(重力や電磁気力などの非接触力)
- 面積力:連続体を要素分割したとき、要素間の境界面を通して働く面積に比例する力(圧力などの接触力)
応力が二階のテンソルであることを示します。
物体全体に働く力\( \bf{ F } \)は、物体内の体積素片\( dV \)に働く単位体積当たりの力ベクトルを\( \bf{ f } \)として
\[
\bf{ F } = \int \bf{ f } dV
\]
で表せます。ベクトル解析のガウスの定理に従い、この体積分は面積分に変換できます。
\[
\begin{align}
\int f_i dV
&= \int \nabla \bf{ \sigma_i } dV
\\
&= \oint \bf{ \sigma_i } \cdot d \bf{ s }
\\
&= \oint \sigma_{ij} \ dS_j
\end{align}
\tag{2.2-1}
\]
\( d \bf{ S } \)は領域上の表面を分割した面積素片ベクトルで、大きさは\( dS \)、向きは表面の外法線に沿うものになります。
\( \sigma_{ij} \ \)は二階のテンソルであり各成分は[N/m2]の単位を持つのでの意味を持つことが分かります。 また、\( \bf{ \sigma_i } \)はi軸方向の応力ベクトルと呼びます。 応力は必ずしも面に垂直な方向のみ作用するわけではなく、面に垂直な方向(面外方向)を法線応力、面内方向を接線応力と呼んで区別します。
なお、応力テンソルが対称テンソルであることは、物体内の要素に働くモーメントから導き出せますが、ここでは割愛します。 詳細は連続体力学ページ3.3節を参照ください。


